Codeforces Round #367 (Div. 2) 题解

本场总结：做了3道，第一题赛后被系统hack

Consider that each of n drivers will move directly to Vasiliy and with a maximum possible speed. Compute the minimum time when Vasiliy will get in any of Beru-taxi cars.

Input

The first line of the input contains two integers a and b ( - 100 ≤ a, b ≤ 100) — coordinates of Vasiliy's home.

The second line contains a single integer n (1 ≤ n ≤ 1000) — the number of available Beru-taxi cars nearby.

The i-th of the following n lines contains three integers xi, yi and vi ( - 100 ≤ xi, yi ≤ 100, 1 ≤ vi ≤ 100) — the coordinates of the i-th car and its speed.

It's allowed that several cars are located at the same point. Also, cars may be located at exactly the same point where Vasiliy lives.

Output

Print a single real value — the minimum time Vasiliy needs to get in any of the Beru-taxi cars. You answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 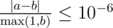$\text{[math]}$ .

Examples

input

output

1.00000000000000000000

input

output

0.50000000000000000000

Note

In the first sample, first taxi will get to Vasiliy in time 2, and second will do this in time 1, therefore 1 is the answer.

In the second sample, cars 2 and 3 will arrive simultaneously.

思路：

水题，但是输出要求精确到小数点后6位，想都没想直接用cout的默认输出，赛后被HACK。

code:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#define maxn 1005
using namespace std;
int main()
{
    double ans,tans;
    double x0,y0,x,y,v;
    cin >> x0 >> y0;
    ans = 100000000;
    //cout << ans << endl;
    int n;
    cin >> n;
    for(int i = 0;i < n;i ++){
        cin >> x >> y >> v;
        double dx,dy;
        dx = x - x0;dy = y - y0;
        tans = sqrt(dx*dx+dy*dy);
        tans /= v;
        if(tans < ans) ans = tans;
    }
    printf("%.8lf\n",ans);
    return 0;
}

View Code

Vasiliy likes to rest after a hard work, so you may often meet him in some bar nearby. As all programmers do, he loves the famous drink "Beecola", which can be bought in n different shops in the city. It's known that the price of one bottle in the shop i is equal to xi coins.

Vasiliy plans to buy his favorite drink for q consecutive days. He knows, that on the i-th day he will be able to spentmi coins. Now, for each of the days he want to know in how many different shops he can buy a bottle of "Beecola".

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 100 000) — the number of shops in the city that sell Vasiliy's favourite drink.

The second line contains n integers xi (1 ≤ xi ≤ 100 000) — prices of the bottles of the drink in the i-th shop.

The third line contains a single integer q (1 ≤ q ≤ 100 000) — the number of days Vasiliy plans to buy the drink.

Then follow q lines each containing one integer mi (1 ≤ mi ≤ 109) — the number of coins Vasiliy can spent on the i-th day.

Output

Print q integers. The i-th of them should be equal to the number of shops where Vasiliy will be able to buy a bottle of the drink on the i-th day.

Example

input

5
3 10 8 6 11
4
1
10
3
11

output

Note

On the first day, Vasiliy won't be able to buy a drink in any of the shops.

On the second day, Vasiliy can buy a drink in the shops 1, 2, 3 and 4.

On the third day, Vasiliy can buy a drink only in the shop number 1.

Finally, on the last day Vasiliy can buy a drink in any shop.

题意：给出n个数字代表一种饮料在n个不同的商店里的价格，给出m个数字主人公在每个店可以使用的钱，问主人公可以在多少个点买到饮料。

思路：排序后二分或树状数组

code:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define maxn 100005
using namespace std;
int price[maxn];
int main()
{
    int n,q;
    scanf("%d",&n);
    for(int i = 0;i < n;i ++) scanf("%d",&price[i]);
    sort(price,price+n);
    scanf("%d",&q);
    for(int i = 0;i < q;i ++){
        int s,e,m,pp;
        scanf("%d",&pp);
        s = 0,e = n - 1;
        while(s <= e){
            m = (s+e) >> 1;
            if(price[m] <= pp) s = m + 1;
            else e = m - 1;
        }
        cout << s << endl;
    }
    return 0;
}

View Code

Vasiliy is fond of solving different tasks. Today he found one he wasn't able to solve himself, so he asks you to help.

Vasiliy is given n strings consisting of lowercase English letters. He wants them to be sorted in lexicographical order (as in the dictionary), but he is not allowed to swap any of them. The only operation he is allowed to do is to reverse any of them (first character becomes last, second becomes one before last and so on).

To reverse the i-th string Vasiliy has to spent ci units of energy. He is interested in the minimum amount of energy he has to spent in order to have strings sorted in lexicographical order.

String A is lexicographically smaller than string B if it is shorter than B (|A| < |B|) and is its prefix, or if none of them is a prefix of the other and at the first position where they differ character in A is smaller than the character in B.

For the purpose of this problem, two equal strings nearby do not break the condition of sequence being sorted lexicographically.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 100 000) — the number of strings.

The second line contains n integers ci (0 ≤ ci ≤ 109), the i-th of them is equal to the amount of energy Vasiliy has to spent in order to reverse the i-th string.

Then follow n lines, each containing a string consisting of lowercase English letters. The total length of these strings doesn't exceed 100 000.

Output

If it is impossible to reverse some of the strings such that they will be located in lexicographical order, print - 1. Otherwise, print the minimum total amount of energy Vasiliy has to spent.

Examples

input

2
1 2
ba
ac

output

input

3
1 3 1
aa
ba
ac

output

input

2
5 5
bbb
aaa

output

-1

input

2
3 3
aaa
aa

output

-1

Note

In the second sample one has to reverse string 2 or string 3. To amount of energy required to reverse the string 3 is smaller.

In the third sample, both strings do not change after reverse and they go in the wrong order, so the answer is - 1.

In the fourth sample, both strings consists of characters 'a' only, but in the sorted order string "aa" should go before string "aaa", thus the answer is - 1.

题意：

给出n个字符串，允许对每个字符串进行逆序排列操作，每次操作对应一个消耗值，求使n个字符串按字典序大小排列的总消耗值，若不可能按字典序排列，输出-1

思路：dp

code:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#define maxn 100005
#define mmax 1e18
using namespace std;
typedef long long ll;
ll dp[maxn][2];
ll c[maxn];
string f(string s){
    string ss;
    for(int i = s.size() - 1;i >= 0;i --){
        ss += s[i];
    }
    return ss;
}
int main()
{
    int n;
    bool done = false;
    string s[maxn];
    cin >> n;
    for(int i = 1;i <= n;i ++) scanf("%d",&c[i]);
    for(int i = 1;i <= n;i ++) cin >> s[i];
    s[0] = "a";
    memset(dp,0,sizeof(dp));
    for(int i = 1;i <= n;i ++ ){
        ll t1,t2,t3,t4;
        dp[i][0] = dp[i][1] = -1;
        t1 = t2 = t3 = t4 = mmax;
        bool flag = false;
        if(dp[i-1][0] >= 0 && s[i].compare(s[i-1]) >= 0) {t1 = dp[i-1][0];flag = true;}
        if(dp[i-1][1] >= 0 && s[i].compare(f(s[i-1])) >= 0) {t2 = dp[i-1][1];flag = true;}
        if(dp[i-1][0] >= 0 && f(s[i]).compare(s[i-1]) >= 0) {t3 = dp[i-1][0] + c[i];flag = true;}
        if(dp[i-1][1] >= 0 && f(s[i]).compare(f(s[i-1])) >= 0) {t4 = dp[i-1][1] + c[i];flag = true;}
        if(!flag) {cout << "-1" << endl;done = true;break;}
        if(t1 != mmax || t2 != mmax) dp[i][0] = min(t1,t2);
        if(t3 != mmax || t4 != mmax) dp[i][1] = min(t3,t4);
    }
    if(!done){
        if(dp[n][0] == -1) cout << dp[n][1] << endl;
        else if(dp[n][1] == -1) cout << dp[n][0] << endl;
        else cout << min(dp[n][0],dp[n][1]) << endl;
    }
    return 0;
}

View Code

Author has gone out of the stories about Vasiliy, so here is just a formal task description.

You are given q queries and a multiset A, initially containing only integer 0. There are three types of queries:

"+ x" — add integer x to multiset A.
"- x" — erase one occurrence of integer x from multiset A. It's guaranteed that at least one x is present in the multiset A before this query.
"? x" — you are given integer x and need to compute the value 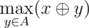$\text{[math]}$ , i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.

Multiset is a set, where equal elements are allowed.

Input

The first line of the input contains a single integer q (1 ≤ q ≤ 200 000) — the number of queries Vasiliy has to perform.

Each of the following q lines of the input contains one of three characters '+', '-' or '?' and an integer xi(1 ≤ xi ≤ 109). It's guaranteed that there is at least one query of the third type.

Note, that the integer 0 will always be present in the set A.

Output

For each query of the type '?' print one integer — the maximum value of bitwise exclusive OR (XOR) of integer xi and some integer from the multiset A.

Example

input

10
+ 8
+ 9
+ 11
+ 6
+ 1
? 3
- 8
? 3
? 8
? 11

output

Note

After first five operations multiset A contains integers 0, 8, 9, 11, 6 and 1.

The answer for the sixth query is integer 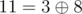$\text{[math]}$ — maximum among integers 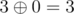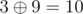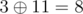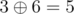$\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ and $\text{[math]}$ .

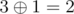题意：

对一个Multiset做基本操作，查询操作要求输出最大的x^b(b属于set）

思路：字典树按二进制存储set中的数字，查询时按照位相反的原则搜索即可。

code:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define maxn 200005
using namespace std;
typedef long long ll;
int c[32];
int a[32];
struct node{
    int cnt;
    node* next[2];
};
int ans;
void init(){
    c[0] = 1;
    for(int i = 1;i < 32;i ++) c[i] = c[i-1]*2;
}
void bulitTree(node* root,int x,bool isAdd){
    if(x == 31) return;
    node *tmp = (node*)malloc(1*sizeof(node));
    tmp->next[0] = tmp->next[1] = NULL;
    tmp->cnt = 0;
    if(a[x] == 0){
        if(!root->next[0]) root->next[0] = tmp;
        root->next[0]->cnt += (isAdd == true?1:-1);
        bulitTree(root->next[0],x+1,isAdd);
    }
    if(a[x] == 1){
        if(!root->next[1]) root->next[1] = tmp;
        root->next[1]->cnt += (isAdd == true?1:-1);
        bulitTree(root->next[1],x+1,isAdd);
    }
}
bool searchTree(node* root,int x){
    if(root == NULL || root->cnt == 0) {return false;}
    if(x == 31 && root->cnt > 0) return true;
    if(a[x] == 0){
        ans += c[30-x];
        if(searchTree(root->next[1],x+1)) return true;
        ans -= c[30-x];
        searchTree(root->next[0],x+1);
    }
    else{
        ans += c[30-x];
        if(searchTree(root->next[0],x+1)) return true;
        ans -= c[30-x];
        searchTree(root->next[1],x+1);
    }
    return true;
}
int main()
{
    int q,x;
    node root;
    root.next[0] = root.next[1] = NULL;
    root.cnt = 1;
    char op;
    cin >> q;
    memset(a,0,sizeof(a));
    init();
    bulitTree(&root,0,true);
    for(int i = 1;i <= q;i ++){
        cin >> op >> x;
        for(int i = 30;i >= 0;i --){
            if(x == 0) a[i] = 0;
            else a[i] = x%2;
            x /= 2;
        }
        if(op == '+') {
            bulitTree(&root,0,true);
        }
        else if(op == '-'){
            bulitTree(&root,0,false);
        }
        else{
            ans = 0;
            searchTree(&root,0);
            cout << ans << endl;
        }
    }
    return 0;
}

View Code

posted on 2016-08-13 01:56 Tob's_the_top 阅读(317) 评论(0) 编辑收藏举报

刷新页面返回顶部

Codeforces Round #367 (Div. 2) 题解

导航

公告