复杂度分析--整理
一、时间复杂度

复杂度量级 粗略地可以分为多项式量级和非多项式量级。其中,非多项式量级只有两个:![]()
我们把时间复杂度为非多项式量级的算法问题叫作 NP(Non--Deterministic Polynomial,非确定多项式)问题。
1. O(1)
1 int i = 8; 2 int j = 6; 3 int sum = i + j;
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是O(1)。
2. O(logn)、O(nlogn)
1 i=1; 2 while (i <= n) { 3 i = i * 2; 4 }
![]()
只要知道 x 值是多少,就知道这行代码执行的次数了,这段代码的复杂度就是![]() 。
。
1 i = i * 2; 2 i = i * 3; 3 . 4 . 5 . 6 i = i * 100;
![]() 等于
等于 ![]() ,O(Cf(n)) = O(f(n)),统一表示为 O(logn)。
,O(Cf(n)) = O(f(n)),统一表示为 O(logn)。
循环执行 n 遍,时间复杂度就是 O(nlogn)。
比如,归并排序、快速排序的时间复杂度都是 O(nlogn)。
3. O(m+n)、O(m*n)
加法法则:如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)),
乘法法则:如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
代码的复杂度由两个数据的规模来决定,无法事先评估 m 和 n 谁的量级大:
修改加法法则为:T1(m) + T2(n) = O(f(m) + g(n))。 乘法法则继续有效:T1(m)*T2(n) = O(f(m)* f(n))。
二、空间复杂度
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。
类比一下,空间复杂度全称就是渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系。
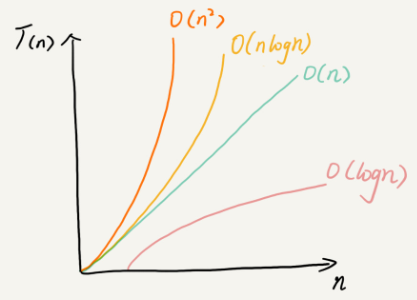
常见的空间复杂度就是 O(1)、O(n)、O(n2 )
三、最好最坏情况时间复杂度
最好情况时间复杂度就是,在最理想的情况下,执行这段代码的时间复杂度。
最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度。
1 // n 表示数组 array 的长度 2 int find(int[] array, int n, int x) { 3 int i = 0; 4 int pos = -1; 5 for (; i < n; ++i) { 6 if (array[i] == x) { 7 pos = i; 8 break; 9 } 10 } 11 return pos; 12 }
平均情况时间复杂度:
有 n+1 种情况:在数组的 0~n-1 位置中和不在数组中,每种情况下,查找需要遍历的元素个数累加起来,
然后再除以 n+1,得到需要遍历的元素个数的平均值,
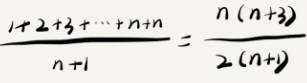
时间复杂度的大 O 标记法中,可以省略掉系数、低阶、常量。简化之后,得到的平均时间复杂度就是 O(n)。
考虑概率进去如下:
假设在数组中与不在数组中的概率都为 1/2。另外,要查找的数据出现在 0~n-1 这 n 个位置的概率也是一样的,为 1/n。

这个值就是概率论中的加权平均值,也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。
去掉系数和常量,这段代码的加权平均时间复杂度仍然是 O(n)。
四、均摊时间复杂度
平均复杂度只在某些特殊情况下才会用到,而均摊时间复杂度应用的场景比它更加特殊、更加有限。

