2016012072+小学四则运算练习软件项目报告

 

Coding.net项目链接：https://git.coding.net/zhangjd725/pwork.git

一、需求分析

1.随机产生n道四则运算的练习题，数字范围 [ 0,100 ]，运算符在3~5之间。

2.不得产生负数及小数，避免重复

3.支持括号，由于运算符较少，故产生2~3个括号，既能达到训练又过于啰嗦

4.支持分数，为了训练化简能力，表达式允许出现非最简分数，而且结果为最简分数，由于小学生能力有限，分数之间不进行乘除运算并且分母大小限制在20以内。

5.习题生成后，将学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中，不要输出额外信息，文件目录与程序目录一致。

6.为了方便分类和筛选，分数运算与普通的四则运算不会同时出现。

二、功能设计

1.为了更好地分类，通过产生随机数的方法让题目之产生分数或无分数的表达式

2.为了避免括号的重复，在保证括号的位置的随机性的前提下，每次产生的括号的位置是递增的，括号后产生的位置比前一个大

3.如果需要，可通过修改几个数值，改变括号的覆盖范围和增加括号的数量（在设计实现中介绍）。

三、设计实现

一个主函数实现数据的输入打印等，通过Expression方法产生表达式，addBracket方法添加括号，toReversePolish方法将中缀表达式

转为后缀表达式，在利用Expression_result计算出结果（不包括分数）。fraction方法产生分数表达式，并计算出结果，加上gcd方法将结果化简。

 

四、算法详解及代码展示

 1.辗转相除法求最大公因数

  具体实现很简单，这里还加了一个判断大小的，以便交换，想要看相关证明的可以看辗转相除法求最大公约数算法证明

 

 public static int gcd(int x,int y)
    {
        if(x<y)
        {
            int temp=x;
            x=y;
            y=temp;
        }
        if(x%y==0)
            return y;
        else
            return gcd(y,x%y);
    }

2.添加括号

left_bracket数组存的是左括号的位置，比如1+3*5-7中数字5的位置就是5，因此会在数字5前加入括号，因此left_bracket数组就把5存进去。可以通过修改left_bracket数组的大小来改变括号数，而如果想增加括号的覆盖范围，即一对括号包含多个运算符，可以对left_bracket数组进行加法+2即距离左括号两个位置，+4距离四个位置，依次类推。

public static Deque<String> addBracket(Deque<String> Q,int OperatorNum)//加括号
    {
        Deque<String> expression_bracket = new LinkedList<String>();;//用于存放带括号的表达式
        int [] left_bracket=new int[3];//括号数
        left_bracket[0]=index[rand.nextInt(2)];//产生第一个左括号的位置
        for(int i=1;i<3;i++)
        {
            left_bracket[i]=left_bracket[i-1]+index2[rand.nextInt(2)];
            while(left_bracket[i]>(OperatorNum-1)*2+1||left_bracket[i]==left_bracket[i-1]+2)
             left_bracket[i]-=2;
        }
                int k=1;
                int i=0;
                while(!Q.isEmpty())
                {
                    if(i<3&&left_bracket[i]==k)//左括号
                    {
                        expression_bracket.offerLast("(");
                        expression_bracket.offerLast(Q.pollFirst());
                        k++;
                        continue;
                    }
                    if(i<3&&left_bracket[i]+2==k)//右括号
                    {
                        expression_bracket.offerLast(Q.pollFirst());
                        expression_bracket.offerLast(")");
                        i++;//下一个括号
                        k++;
                        continue;
                    }
                    
                    expression_bracket.offerLast(Q.pollFirst());
                    k++;
                }
            return expression_bracket;
    }

3.转为逆波兰表达式

转化的步骤可以看博客：前缀、中缀、后缀表达式(逆波兰表达式),很不错的文章，我就是按他的步骤写的，但是他的代码我看不懂，所以我就按他的步骤写了一遍，我建议如果判断字符串的值是否相等时用equals否则可能出现问题。

public static Deque<String> toReversePolish(Deque<String> Q)//转后缀表达式
{
    Deque<String> s1=new LinkedList<String>();
    Deque<String> s2=new LinkedList<String>();
    while(!Q.isEmpty())
    {
        String temp=Q.pollFirst();
        try{
            int num=Integer.parseInt(temp);
            s2.offerLast(String.valueOf(num));
        }
        catch(Exception e)
        {
            if(temp=="(")//遇到左括号
            {
                s1.offerLast("(");
            }
            else if(temp==")")//遇到右括号
            {
                while(s1.peekLast()!="(")
                {

                    s2.offerLast(s1.pollLast());
                }
                s1.pollLast();
            }
            else//遇到运算符
            {
                while(temp!="?")
                {
                    if(s1.isEmpty()||s1.peekLast().equals("("))
                    {
                        s1.offerLast(temp);
                        temp="?";//表明temp进栈
                    }
                    else if((temp.equals("*")||temp.equals("÷"))&&(s1.peekLast().equals("+")||s1.peekLast().equals("-")))
                    {
                        s1.offerLast(temp);
                        temp="?";
                    }
                    else
                    {
                        s2.offerLast(s1.pollLast());
                    }

                }
            }
        }
    }
    while(!s1.isEmpty())
        s2.offerLast(s1.pollLast());
    return s2;
}

 

4.求表达式结果

这个其实也很简单，代码参考图解后缀表达式的计算过程，相信看了这篇博客自己都会写了。

public static int Expression_result(Deque<String> Q)//求结果
{
    Stack<Integer> res = new Stack<Integer>();
    while(!Q.isEmpty())
    {
        String temp=Q.pollFirst();
        if(temp.equals("+"))
        {
            int num1=res.pop();
            int num2=res.pop();
            res.push(num2+num1);
            continue;
        }
        if(temp.equals("-"))
        {
            int num1=res.pop();
            int num2=res.pop();
            if(num2-num1<0)
                return -1;
            res.push(num2-num1);
            continue;
        }
        if(temp.equals("*"))
        {
            int num1=res.pop();
            int num2=res.pop();
            res.push(num2*num1);
            continue;
        }
        if(temp.equals("÷"))
        {
            int num1=res.pop();
            int num2=res.pop();
            if(num1==0||num2%num1!=0)
                return -1;
            res.push(num2/num1);
            continue;
        }
        int num=Integer.parseInt(temp);
        res.push(num);
    }
    return res.pop();
}

 

 

五、测试运行

 

 

 

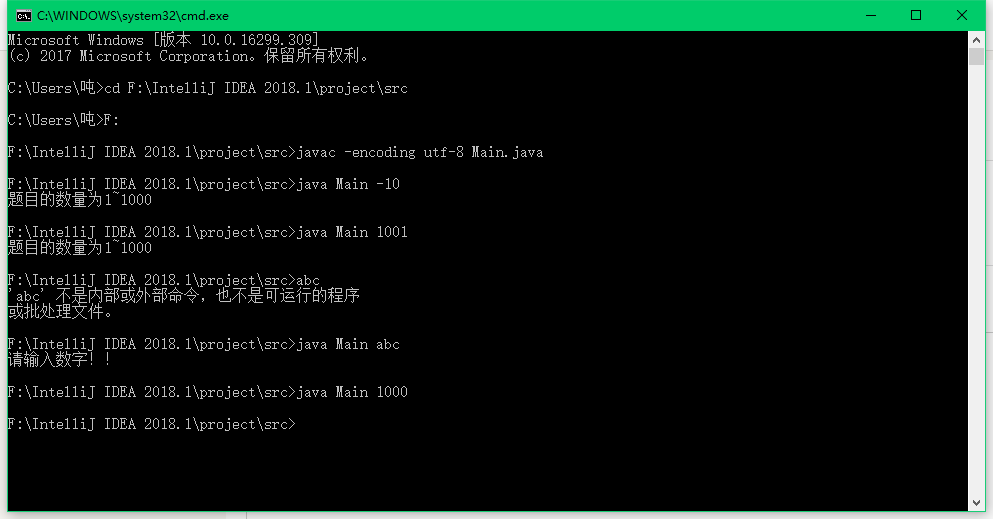
六、总结

       这个作业其实不需要那么多的时间的，只是分析设计的做的不够好，导致运行结果不符合要求，也不能让自己满意。比如括号的位置及生成的数量，本来是希望越随机越好，结果就是很乱，后来通过限制括号的位置，就很好的解决，而且并不影响小学生对习题难度的需求。还有就是对java的不熟悉，因为这个花了将近一半的时间去修改调试，比如我在写中缀表达式转后缀表达式时，判断字符串相等时用“==”，有些情况得不到想要的结果，而用“equals”就能解决，这个就浪费我大量的时间，而我本可以用这个时间去将我的代码做的更好。这个我虽然百度了相关解释，但是我还是有点不解。希望能在实际操作中能够慢慢理解。写完这篇博客感觉一切都放下了，终于可以好好休息了。

七、PSP

 

PSP	任务内容	计划共完成需要的时间(h)	实际完成需要的时间(h)
Planning	计划	1	2
·        Estimate	·   估计这个任务需要多少时间，并规划大致工作步骤	0.5	3
Development	开发	20	40
·        Analysis	·         需求分析 (包括学习新技术)	2	5
·        Design Spec	·         生成设计文档	2	2
·        Design Review	·         设计复审 (和同事审核设计文档)	1	0.5
·        Coding Standard	·         代码规范 (为目前的开发制定合适的规范)	1	3
·        Design	·         具体设计	5	6
·        Coding	·         具体编码	20	40
·        Code Review	·         代码复审	1	1
·        Test	·         测试（自我测试，修改代码，提交修改）	5	20
Reporting	报告	6	8
·         Test Report	·         测试报告	2	4
·         Size Measurement	·         计算工作量	1	2
·         Postmortem & Process Improvement Plan	·         事后总结, 并提出过程改进计划	3	5