回溯法常见题目总结
1.电话号码的字母组合
题目描述:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。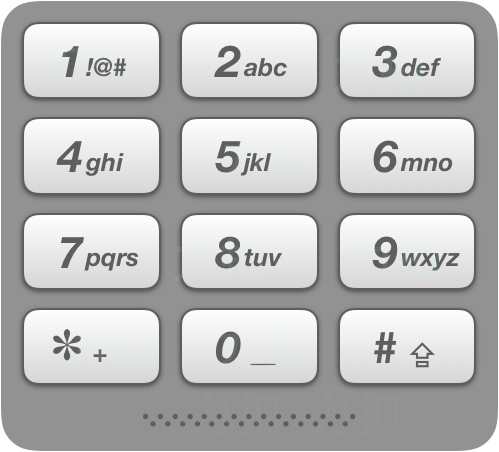
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:
尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
实现代码:
class Solution {
public:
vector<string> letterCombinations(string digits) {
if(digits == ""){
return res;
}
letter(digits,0,"");
return res;
}
private:
string lett[10] = {
" ",
"",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
};
vector<string>res;
void letter(string digits,int index,string s){
if(index == digits.size()){
res.push_back(s);
return;
}
char c = digits[index];
string letters = lett[c - '0'];
for(int i = 0;i < letters.size();i++){
letter(digits,index + 1,s + letters[i]);
}
return;
}
};
2.括号生成
题目描述:
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
实现代码:
class Solution {
public:
vector<string> generateParenthesis(int n) {
if(n == 0){
return res;
}
generate("",n,0,0);
return res;
}
private:
vector<string>res;
void generate(string str,int n,int left,int right){
if(right == n){
res.push_back(str);
return;
}
if(left < n){
generate(str + "(",n,left + 1,right);
}
if(left > right){
generate(str + ")",n,left,right + 1);
}
return;
}
};
3.组合总数
题目描述:
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
实现代码:
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>>res;
vector<int>tmp;
int start = 0;
combination(candidates,target,0,tmp,res);
return res;
}
private:
void combination(vector<int>& candidates,int target,int start,vector<int>& tmp,vector<vector<int>>& res){
if(target == 0){
res.push_back(tmp);
return;
}
for(int i = start;i < candidates.size();i++){
if(target > 0){
tmp.push_back(candidates[i]);
combination(candidates,target - candidates[i],i,tmp,res);
tmp.pop_back();
}
if(target < 0){
return;
}
}
}
};
4.组合总数Ⅱ
题目描述:
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
实现代码:
class Solution {
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target)
{
vector<int> item;
vector<vector<int>> res;
sort(candidates.begin(),candidates.end());
backTarget(candidates,0,target,item,res);
return res;
}
void backTarget(vector<int> candidates, int start,int target,vector<int> item,vector<vector<int>> &res){
if(target<0){
return ;
}
if(target==0){
res.push_back(item);
}
for(int i=start;i<candidates.size();i++){
if(i>start&&candidates[i]==candidates[i-1]){
continue;
}
item.push_back(candidates[i]);
backTarget(candidates,i+1,target-candidates[i],item,res);
item.pop_back();
}
}
};
5.全排列
题目描述:
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
实现代码:
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
if(nums.size() == 0){
return res;
}
stat = vector<bool>(nums.size(),false);
generatePermute(nums,0,p);
return res;
}
private:
vector<vector<int>> res;
vector<int>p;
vector<bool>stat;
void generatePermute(vector<int> &nums,int index,vector<int> p){
if(index == nums.size()){
res.push_back(p);
return;
}
for(int i = 0;i < nums.size();i++){
if(!stat[i]){
p.push_back(nums[i]);
stat[i] = true;
generatePermute(nums,index + 1,p);
p.pop_back();
stat[i] = false;
}
}
return;
}
};
6.全排列Ⅱ
题目描述:
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
实现代码:
class Solution {
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>>res1;
if(nums.size() < 0){
return res1;
}
visited = vector<bool>(nums.size(),false);
vector<int>tmp;
int k = 0;
permute(nums,k,tmp);
res1.assign(res.begin(),res.end());
return res1;
}
private:
set<vector<int>>res;
vector<bool>visited;
void permute(vector<int>&nums,int k,vector<int>& tmp){
if(k == nums.size()){
res.insert(tmp);
return;
}
for(int i = 0;i < nums.size();i++){
if(!visited[i]){
visited[i] = true;
tmp.push_back(nums[i]);
permute(nums,k + 1,tmp);
tmp.pop_back();
visited[i] = false;
}
}
return;
}
};
7.组合
题目描述:
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
实现代码:
class Solution {
public:
vector<vector<int>> combine(int n, int k) {
if(n == 0||k == 0||k > n){
return res;
}
vector<int>p;
generateCombine(n,k,1,p);
return res;
}
private:
vector<vector<int>> res;
void generateCombine(int n,int k,int start,vector<int> p){
if(k == p.size()){
res.push_back(p);
return;
}
for(int i = start;i <= n;i++){
p.push_back(i);
generateCombine(n,k,i + 1,p);
p.pop_back();
}
return;
}
};
8.子集
题目描述:
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
实现代码:
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
if(nums.size() == 0){
return res;
}
res.push_back(tmp);
subset(nums,0,tmp);
return res;
}
private:
vector<vector<int>> res;
vector<int> tmp;
void subset(vector<int> &nums,int start,vector<int> tmp){
if(start == nums.size()){
return;
}
for(int i = start;i < nums.size();i++){
tmp.push_back(nums[i]);
res.push_back(tmp);
subset(nums,i + 1,tmp);
tmp.pop_back();
}
}
};
9.子集Ⅱ
题目描述:
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
实现代码:
class Solution {
public:
void dfs(vector<int>& nums, int pos, vector<int>& path, vector<vector<int>>& result)
{
for(int i = pos; i < nums.size(); i ++)
{
if(i > pos && nums[i] == nums[i-1])
continue;
path.push_back(nums[i]);
result.push_back(path);
dfs(nums, i + 1, path, result);
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
result.push_back(path);
if(nums.empty()) return result;
sort(nums.begin(), nums.end());
dfs(nums, 0, path, result);
return result;
}
};
10单词搜索
题目描述:
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board =
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.
实现代码:
class Solution {
private:
int d[4][2] = {{-1,0},{1,0},{0,-1},{0,1}};
int m,n;
bool inArea(int x,int y){
return x >= 0 && x < m && y >= 0 && y < n;
}
vector<vector<bool>> tmp;
bool isExist(vector<vector<char>>& board,string word,int index,int startx,int starty){
if(index == word.size() - 1){
return board[startx][starty] == word[index];
}
if(board[startx][starty] == word[index]){
tmp[startx][starty] = true;
for(int i = 0;i < 4;i++){
int newx = startx + d[i][0];
int newy = starty + d[i][1];
if(inArea(newx,newy) && tmp[newx][newy] == false){
if(isExist(board,word,index + 1,newx,newy)){
return true;
}
}
}
tmp[startx][starty] = false;
}
return false;
}
public:
bool exist(vector<vector<char>>& board, string word) {
m = board.size();
n = board[0].size();
tmp = vector<vector<bool>>(m,vector<bool>(n,false));
for(int i = 0;i < board.size();i++){
for(int j = 0;j < board[i].size();j++){
if(isExist(board,word,0,i,j)){
return true;
}
}
}
return false;
}
};
11.岛屿数量
题目描述:
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
实现代码:
class Solution {
private:
int d[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
vector<vector<bool>>visited;
int m,n;
bool inArea(int x,int y){
return x >= 0 && x < m && y >= 0 && y < n;
}
void dfs(vector<vector<char>> &grid,int startx,int starty){
visited[startx][starty] = true;
for(int i = 0;i < 4;i++){
int newx = startx + d[i][0];
int newy = starty + d[i][1];
if(inArea(newx,newy) && !visited[newx][newy] && grid[newx][newy] == '1'){
dfs(grid,newx,newy);
}
}
return;
}
public:
int numIslands(vector<vector<char>>& grid) {
m = grid.size();
if(m == 0){
return 0;
}
n = grid[0].size();
int res = 0;
visited = vector<vector<bool>>(m,vector<bool>(n,false));
for(int i = 0;i < grid.size();i++){
for(int j = 0;j < grid[i].size();j++){
if(grid[i][j] == '1' && !visited[i][j]){
res++;
dfs(grid,i,j);
}
}
}
return res;
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号