【学习笔记】非监督学习-k-means

目录

• k-means
• k-means API
  • k-means对Instacart Market用户聚类
  • Kmeans性能评估指标
  • Kmeans性能评估指标API
• Kmeans总结

无监督学习，顾名思义，就是不受监督的学习，一种自由的学习方式。该学习方式不需要先验知识进行指导，而是不断地自我认知，自我巩固，最后进行自我归纳，在机器学习中，无监督学习可以被简单理解为不为训练集提供对应的类别标识（label），其与有监督学习的对比如下： 有监督学习（Supervised Learning）。

在有监督学习中，我们把对样本进行分类的过程称之为分类（Classification），而在无监督学习中，我们将物体被划分到不同集合的过程称之为聚类（Clustering）。

k-means

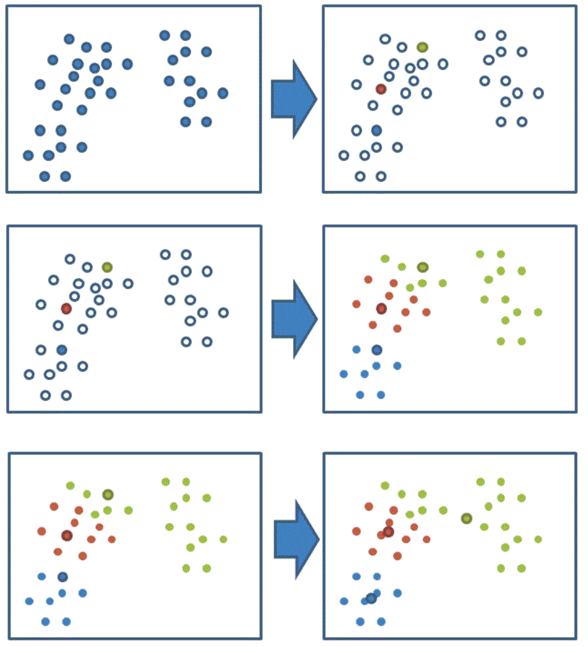
K-means通常被称为劳埃德算法，这在数据聚类中是最经典的，也是相对容易理解的模型。算法执行的过程分为4个阶段。

• 1、随机设置K个特征空间内的点作为初始的聚类中心
• 2、对于其他每个点计算到K个中心的距离，从中选出距离最近的⼀个点作为⾃⼰的标记
• 3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）
• 4、如果计算得出的新中心点与原中心点一样，那么结束，否则重新进行第二步过程

k-means API

sklearn.cluster.KMeans(n_clusters=8,init='k-means++')

• k-means聚类
• n_clusters:开始的聚类中心数量
• init:初始化方法，默认为'k-means ++'
• labels_:默认标记的类型，可以和真实值比较（不是值比较）

k-means对Instacart Market用户聚类

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

products = pd.read_csv('data/instacart-market-basket-analysis/products.csv')
order_products__prior = pd.read_csv('data/instacart-market-basket-analysis/order_products__prior.csv', nrows=3000000)
orders = pd.read_csv('data/instacart-market-basket-analysis/orders.csv', nrows=3000000)
aisles = pd.read_csv('data/instacart-market-basket-analysis/aisles.csv')

# merge the four 
_mg = pd.merge(order_products__prior, products, on=['product_id', 'product_id'])
_mg = pd.merge(_mg, orders, on=['order_id', 'order_id'])
mt = pd.merge(_mg, aisles, on=['aisle_id', 'aisle_id'])

cross = pd.crosstab(mt['user_id'], mt['aisle'])

# 降纬
pca = PCA(n_components=0.9)
data = pca.fit_transform(cross)

# 把样本数量减少
x = data[:1000]

km = KMeans(n_clusters=4)
km.fit(x)
predict = km.predict(x)

plt.figure(figsize=(20, 8))
colored = ['orange', 'green', 'blue', 'red']
colr = [colored[i] for i in predict]

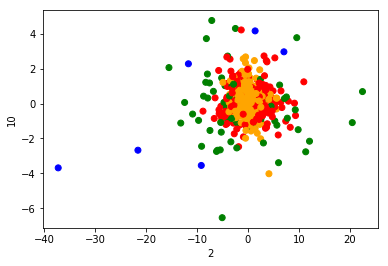
plt.scatter(x[:, 1], x[:, 20], color=colr)
plt.xlabel("2")
plt.ylabel("10")

plt.show()

运行结果：

Kmeans性能评估指标

Kmeans性能评估指标API

sklearn.metrics.silhouette_score(X, labels)

• 计算所有样本的平均轮廓系数
• X：特征值
• labels：被聚类标记的目标值

计算上例中的轮廓系数：

# 轮廓系数
silhouette_score(x, predict)

输出结果：

0.32277181074848377

Kmeans总结

特点分析：采用迭代式算法，直观易懂并且非常实用

缺点：容易收敛到局部最优解(多次聚类)
需要预先设定簇的数量(k-means++解决)