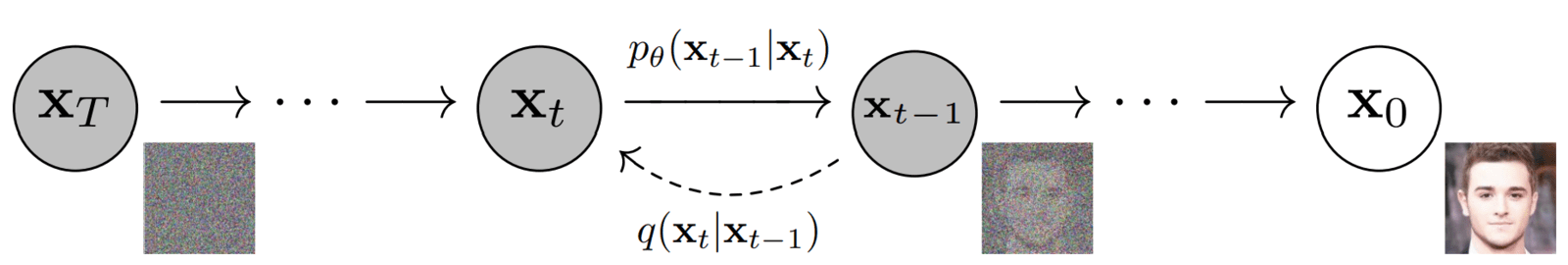InDepth Guide to Denoising Diffusion Probabilistic Models DDPM：DDPM扩散概率模型去噪深度指南——理论到实现

An In-Depth Guide to Denoising Diffusion Probabilistic Models DDPM – Theory to Implementation
中文翻译：DDPM扩散概率模型去噪深度指南——理论到实现

https://learnopencv.com/denoising-diffusion-probabilistic-models/#forward-diffusion-equation

https://github.com/spmallick/learnopencv/tree/master/Guide-to-training-DDPMs-from-Scratch

扩散概率模型是一个令人兴奋的新研究领域，在图像生成方面显示出巨大的前景。回想起来，基于扩散的生成模型于2015年首次引入，并于2020年推广，当时Ho等人发表了论文“去噪扩散概率模型”（DDPM）。DDPM负责使扩散模型实用。在本文中，我们将重点介绍DDPM背后的关键概念和技术，并在“花”数据集上从头开始训练DDPM，以实现无条件图像生成。

无条件图像生成

在DDPM中，作者改变了公式和模型训练程序，这有助于提高和实现与GAN相媲美的“图像保真度”，并确立了这些新生成算法的有效性。

完全理解“去噪扩散概率模型”的最佳方法是复习理论（+一些数学）和底层代码。考虑到这一点，让我们探索学习路径，其中：

我们将首先解释什么是生成模型以及为什么需要它们。
我们将从理论的角度讨论基于扩散的生成模型中使用的方法
我们将探索理解去噪扩散概率模型所需的所有数学。
最后，我们将讨论DDPM中用于图像生成的训练和推理，并在PyTorch中从头开始进行编码。

1. 生成模型的必要性

基于图像的生成模型的工作是生成相似的新图像，换句话说，是我们原始图像集的“代表”。

我们需要创建和训练生成模型，因为可以用（256x256x3）图像表示的所有可能图像的集合是巨大的。图像必须具有正确的像素值组合来表示有意义的东西（我们可以理解的东西）。

An RGB image of a Sunflower

例如，为了使上面的图像代表“向日葵”，图像中的像素需要处于正确的配置中（它们需要具有正确的值）。而这些图像存在的空间只是（256x256x3）图像空间所表示的整个图像集的一小部分。

现在，如果我们知道如何从这个子空间中获取/采样一个点，我们就不需要构建“生成模型”。然而，在这个时间点，我们不需要。😓

捕获/建模这个（数据）子空间的概率分布函数，或者更确切地说，概率密度函数（PDF）仍然未知，很可能太复杂而没有意义。

这就是为什么我们需要“生成模型”来计算我们的数据满足的潜在似然函数。

PS：PDF是一个“概率函数”，表示连续随机变量的密度（似然性），在这种情况下，这意味着一个函数表示图像位于函数参数定义的特定值范围之间的似然性。

PPS：每个PDF都有一组参数，用于确定分布的形状和概率。分布的形状随着参数值的变化而变化。例如，在正态分布的情况下，我们有均值\(µ\)（mu）和方差\(σ^2\)（sigma）来控制分布的中心点和扩散。

Effect of parameters of the Gaussian Distribution

Source: https://magic-with-latents.github.io/latent/posts/ddpms/part2/

2. 什么是扩散概率模型？

在我们之前的文章“图像生成扩散模型简介”中，我们没有讨论这些模型背后的数学。我们只提供了扩散模型如何工作的概念性概述，并重点介绍了不同的知名模型及其应用。在本文中，我们将主要关注第一部分。

在本节中，我们将从逻辑和理论的角度解释基于扩散的生成模型。接下来，我们将回顾从头开始理解和实现去噪扩散概率模型所需的所有数学。

扩散模型是一类受非平衡统计物理学思想启发的生成模型，该思想指出：

我们可以使用马尔可夫链逐步将一种分布转换为另一种分布

—— 使用非平衡热力学的深度无监督学习，2015年

扩散生成模型由两个相反的过程组成，即正向和反向扩散过程。

2.1 正向扩散过程

“破坏容易，创造难”

—— 赛珍珠

在“正向扩散”过程中，我们缓慢迭代地向训练集中的图像添加噪声（破坏），使它们“移出或远离”现有的子空间。
我们在这里所做的是将我们的训练集所属的未知和复杂的分布转换为一个易于我们采样和理解的（数据）点。
在正向过程结束时，图像变得完全无法识别。复杂的数据分布被完全转化为（选定的）简单分布。每个图像都被映射到数据子空间之外的空间。

Source: https://ayandas.me/blog-tut/2021/12/04/diffusion-prob-models.html

2.2 反向扩散过程

通过将图像形成过程分解为去噪自编码器的顺序应用，扩散模型（DM）在图像数据及其他方面实现了最先进的合成结果。

——稳定扩散，2022年

A high-level conceptual overview of the entire image space.

在“反向扩散过程”中，其思想是逆转正向扩散过程。
我们缓慢而迭代地尝试逆转正向过程中对图像执行的损坏。
反向过程从正向过程结束的地方开始。
从一个简单的空间开始的好处是，我们知道如何从这个简单的分布中获取/采样一个点（可以把它想象成数据子空间之外的任何点）。
我们的目标是找出如何返回数据子空间。
然而，问题是，我们可以从这个“简单”空间中的一个点开始走无限的路径，但只有其中的一小部分会把我们带到“数据”子空间。
在扩散概率模型中，这是通过参考正向扩散过程中采取的小迭代步骤来实现的。
满足正向过程中损坏图像的PDF在每一步都略有不同。
因此，在反向过程中，我们在每一步都使用深度学习模型来预测正向过程的PDF参数。
一旦我们训练了模型，我们就可以从简单空间中的任何一点开始，并使用模型迭代地采取步骤，将我们带回数据子空间。
在反向扩散中，我们从有噪声的图像开始，逐步迭代地执行“去噪”。
这种训练和生成新样本的方法比GAN更稳定，也比变分自编码器（VAE）和归一化流等以前的方法更好。

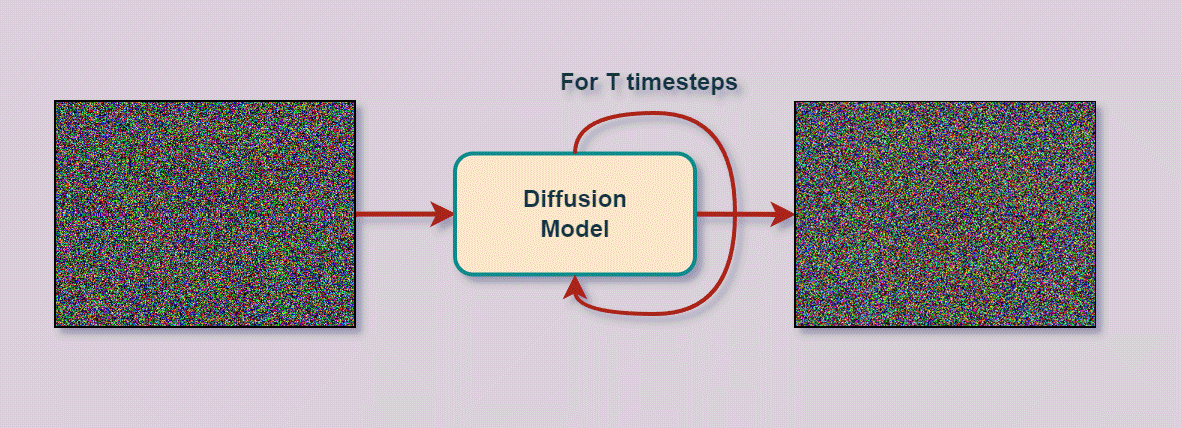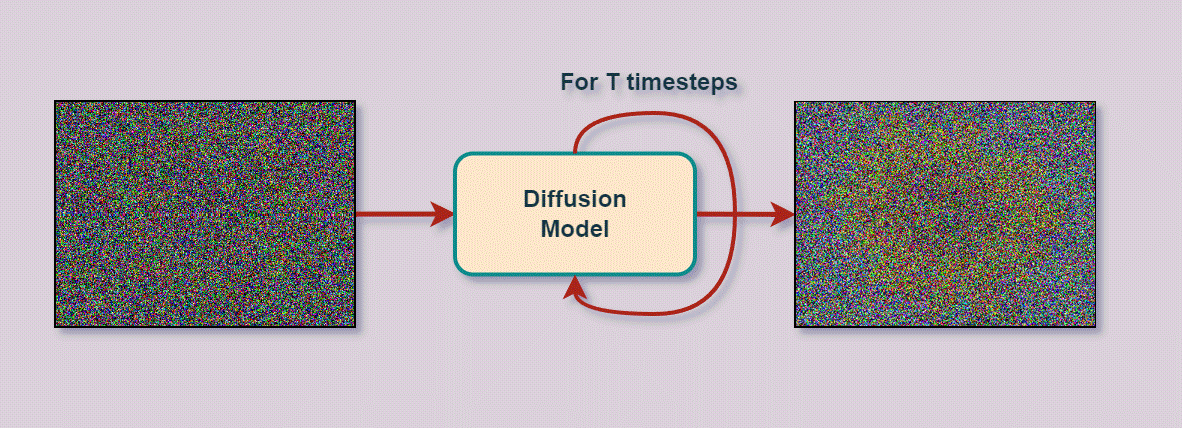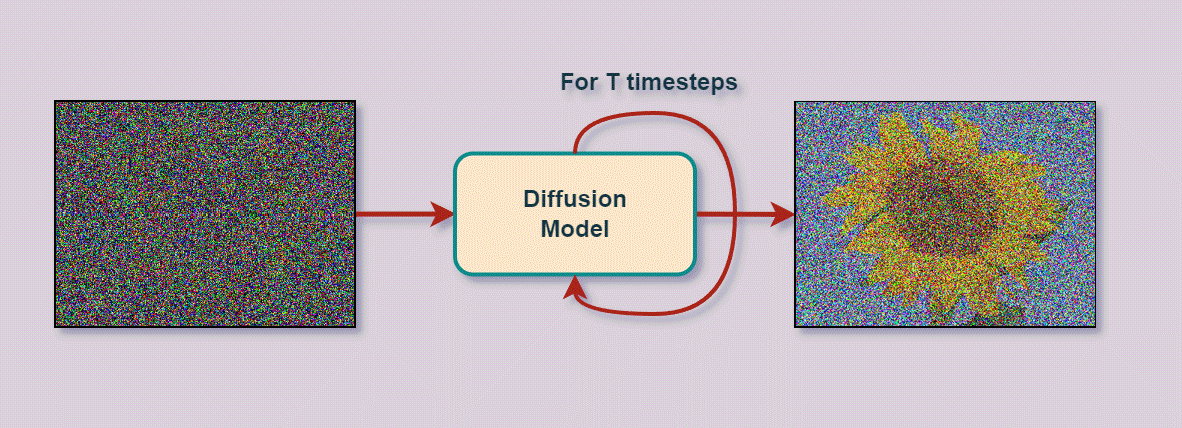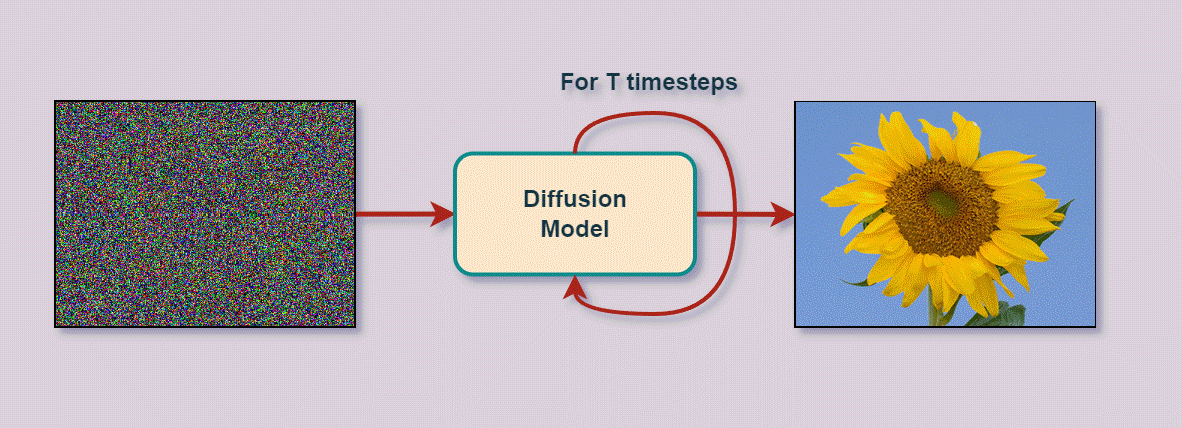
A gif illustrating the inference stage of diffusion probabilistic models.

自2020年推出以来，DDPM一直是尖端图像生成系统的基础，包括DALL-E 2、Imagen、Stable Diffusion和Midjourney。

随着当今人工智能艺术生成工具的大量出现，很难为特定的用例找到合适的工具。在我们最近的文章中，我们探讨了所有不同的人工智能艺术生成工具，以便您可以做出明智的选择来生成最好的艺术。

3. 去噪扩散概率模型背后的数学细节

由于这篇文章背后的动机是“从头开始创建和训练去噪扩散概率模型”，我们可能不得不介绍它们背后的数学魔法，而不是全部。

在本节中，我们将介绍所有必需的数学，同时确保它也易于理解。

让我们开始…

箭头上提到了两个术语：

\(q(x_{t}|x_{t-1})\)
1. 这个术语也被称为前向扩散核（FDK）。
2. 它定义了给定图像xt-1的正向扩散过程xt中时间步长t处图像的PDF。
3. 它表示正向扩散过程中每一步应用的“过渡函数”。
\(p_{\theta}(x_{t-1}|x_{t})\)
1. 与正向过程类似，它被称为反向扩散核（RDK）。
2. 它代表\(x_{t-1}\)的PDF，其中\(x_t\)由\(𝜭\)参数化。\(\theta\)表示使用神经网络学习反向过程分布的参数。
3. 这是反向扩散过程中每一步应用的“过渡函数”。

3.1 正向扩散过程的数学细节

正向扩散过程中的分布\(q\)定义为马尔可夫链，由下式给出：

\[q(x_{1},\ldots,x_{T}|x_{0}):=\prod_{t=1}^{T}q(x_{t}|x_{t-1})\ldots(1)\\q(x_{t}|x_{t-1}):=\mathcal{N}(x_{t};\sqrt{1-\beta_{t}}x_{t-1},\beta_{t}I)\quad\ldots(2) \]

我们首先从数据集中获取一张图像：\(x_0\)。从数学上讲，它被表述为从原始（但未知）数据分布中采样一个数据点：\(x_{0}\sim q(x_{0})\)。
正向过程的PDF是从时间步\(1→T\)开始的个体分布的产物
正向扩散过程是固定且已知的。
从时间步长\(1\)到\(T\)的所有中间噪声图像也称为“延迟”。延迟的维度与原始图像相同。
用于定义FDK的PDF是“正态/高斯分布”（方程式2）。
在每个时间步长\(t\)，定义图像\(x_t\)分布的参数设置为：
- 平均值：\(\sqrt{1-\beta_{t}} x_{t-1}\)
- 协方差：\(\beta_{t}I\)
术语\(β\)被称为“扩散率”，并使用“方差调度器”预先计算。术语\(I\)是一个恒等矩阵。因此，每个时间步长的分布称为各向同性高斯分布。
原始图像在每个时间步长都会因添加少量高斯噪声（\(\epsilon\)）而损坏。添加的噪声量由调度器调节。
通过选择足够大的时间步长并定义一个行为良好的\(\beta_t\)调度，重复应用FDK逐渐将数据分布转换为近似各向同性高斯分布。

我们如何从\(x_{t-1}\)中获得图像\(x_t\)，以及如何在每个时间步长添加噪声？

通过在变分自编码器中使用重参数化技巧，可以很容易地理解这一点。

参考第二个方程，我们可以很容易地从正态分布中采样图像\(x_t\)，如下所示：

\[\begin{aligned}x_{t}&=\sqrt{1-\beta_{t}} x_{t-1}+\sqrt{\beta_{t}} \epsilon\quad\ldots(3)\\&;\mathrm{where}\ \epsilon\sim\mathcal{N}(0,I)\end{aligned} \]

这里，\(\epsilon\)是从标准高斯分布中随机采样的“噪声”项，首先进行缩放，然后添加（缩放）\(x_{t-1}\)。
这样，从\(x_0\)开始，原始图像从\(t=1…T\)迭代地被破坏

在实践中，DDPM的作者使用“线性方差调度器”，在\([0.001,\ldots,0.02]\)范围内定义\(\beta\)，并设置总时间步长\(T=1000\)

“扩散模型通过每个正向过程步骤（按因子）缩小数据，这样在添加噪声时方差就不会增加。”

—— 去噪扩散概率模型，2020年

Variance Scheduler vs timesteps

这里有一个问题，导致正向扩散过程效率低下🐢.

每当我们需要时间步长\(t\)的潜在样本\(x_t\)时，我们必须在马尔可夫链中执行\(t-1\)步。

We have to follow through all \(t-1\)intermediate states in Markov Chain to get\(x_t\)

为了解决这个问题，DDPM的作者重新制定了内核，使其在过程中直接从时间步长\(0\)（即从原始图像）变为时间步长\(t\)。

Skipping intermediate steps

为此，定义了两个附加术语：

\[\alpha_{t}:= 1-\beta_{t}\quad\ldots(4)\\\bar{\alpha}_{t}:=\prod_{s=1}^{t}\alpha_{s}\quad\ldots(5) \]

其中式（5）是从\(1\)到\(T\)的\(𝛂\)的累积乘积。

然后，通过将\(𝝱'\)替换为\(𝛂'\)，并利用高斯分布的加法性质。正向扩散过程可以改写为\(𝛂\)：

\[\begin{aligned}q(x_{t}|x_{0})&:=\mathcal{N}(x_{t};\sqrt{\bar{\alpha}_{t}}x_{0},(1-\bar{\alpha}_{t})I)\quad\ldots(6)\\x_{t}&:=\sqrt{\bar{\alpha}_{t}}x_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon\end{aligned} \]

🚀 使用上述公式，我们可以在马尔可夫链中的任意时间步长\(t\)进行采样。

这就是正向扩散过程。

3.2 反向扩散过程的数学细节

Czech Hiking Markers System. Following the path to take in the return journey.

“在反向扩散过程中，任务是学习正向扩散过程的有限时间（在\(T\)个时间步长内）反转。”

这基本上意味着我们必须“撤消”正向过程，即迭代地去除正向过程中添加的噪声。这是使用神经网络模型完成的。

在正向过程中，转换函数\(q\)是使用高斯函数定义的，那么反向过程\(p\)应该使用什么函数呢？神经网络应该学习什么？

1949年，W.Feller证明，对于高斯（和二项式）分布，扩散过程的反转与正向过程具有相同的函数形式。
这意味着，与定义为正态分布的FDK类似，我们可以使用相同的函数形式（高斯分布）来定义反向扩散核。
反向过程也是马尔可夫链，其中神经网络在每个时间步预测反向扩散核的参数。
在训练过程中，学习到的（参数的）估计值应接近FDK在每个时间步的后验参数。我们将在下一节中更多地讨论FDK的后验。
我们想要这样做，因为如果我们反向遵循正向轨迹，我们可能会回到原始数据分布。
在此过程中，我们还将学习如何从纯高斯噪声开始生成与底层数据分布紧密匹配的新样本（我们在推理过程中无法访问正向过程）。

A modified illustration of diffusion process focusing on reverse diffusion process.

反向扩散的马尔可夫链从正向过程结束的地方开始，即在时间步长\(T\)处，数据分布已被转换为（几乎）各向同性高斯分布。

\[q(x_{T})\approx\mathcal{N}(x_{t};0,I)\\p(x_{T}):=\mathcal{N}(x_{l};0,I)\ldots(7) \]
反向扩散过程的PDF是我们从纯噪声\(x_T\)开始得到数据样本（与原始分布相同）的所有可能路径的“积分”。

\[p_\theta(x_0):=\int p_\theta(x_{0:T})dx_{1:T} \]
\[p_{\theta}(\mathbf{x}_{0:T}):=p(\mathbf{x}_{T})\prod_{t=1}^{T}p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}),\quad p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}):=\mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta}(\mathbf{x}_{t},t),\Sigma_{\theta}(\mathbf{x}_{t},t)) \]

All equations related to the forward and reverse diffusion processes.

3.3 用于去噪扩散概率模型的训练目标和损失函数

基于扩散的生成模型的训练目标相当于“最大化（在反向过程结束时）生成的样本（\(x\)）属于原始数据分布的对数似然”

我们将扩散模型中的转换函数定义为“高斯函数”。为了最大化高斯分布的对数似然性，需要尝试找到分布的参数（\(𝞵\)，\(𝝈^2\)），使（生成的）数据与原始数据属于相同数据分布的“似然性”最大化。

为了训练我们的神经网络，我们将损失函数（\(L\)）定义为目标函数的负值。因此，\(p_{\theta}(x_{0})\)的高值意味着低损失，反之亦然。

\[p_{\theta}(x_{0}):=\int p_{\theta}(x_{0:T})dx_{1:T}\\L=-log(p_{\theta}(x_{0})) \]

事实证明，这很难解决，因为我们需要在非常高的维度（像素）空间上对\(T\)时间步长上的连续值进行积分。

相反，作者从VAE中汲取灵感，使用变分下限（VLB）重新制定训练目标，也称为“证据下限”（ELBO），这是一个看起来很可怕的方程👻

\[\mathbb{E}\left[-\log p_\theta(\mathbf{x}_0)\right]\leq\mathbb{E}_q\left[-\log\frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}|\mathbf{x}_0)}\right]=\mathbb{E}_q\left[-\log p(\mathbf{x}_T)-\sum_{t\geq1}\log\frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\right]=:L \]

Prof. Andrew Ng to the rescue 🐱‍🏍

经过一些简化，DDPM作者得出了这个最终的\(L_{vlb}\)——变分下限损失项：

\[\mathbb{E}_{q}\bigg[\underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_{T}|\mathbf{x}_{0})\parallel p_{\theta}(\mathbf{x}_{T}))}_{L_{T}}+\sum_{t>1}\underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})\parallel p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}))}_{L_{t-1}}\underbrace{-\log p_{\theta}(\mathbf{x}_{\theta}|\mathbf{x}_{1})}_{L_{0}}\bigg] \]

我们可以将上述\(L_{vlb}\)损失项分解为单独的时间步长，如下所示：

\[\begin{aligned} L_{\mathrm{vlb}}& :=L_0+L_1+...+L_{T-1}+L_T \\ L_{0}& :=-\log p_\theta(x_0|x_1) \\ L_{t-1}& :=D_{KL}(q(x_{i-1}|x_{i},x_{0})\parallel p_{\theta}(x_{i-1}|x_{i})) \\ L_{T}& :=D_{KL}(q(x_{T}|x_{0})\parallel p(x_{T})) \end{aligned} \]

你可能会注意到这个损失函数是巨大的！但DDPM的作者通过忽略简化损失函数中的一些项进一步简化了它。

被忽略的项包括：

\(L_0\)——作者在没有这个的情况下获得了更好的结果。
\(L_T\)——这是正向过程中最终潜分布和反向过程中第一个潜分布之间的“KL散度”。然而，这里没有涉及神经网络参数，所以我们除了定义一个好的方差调度器并使用大的时间步长外，什么也做不了，这样它们都表示各向同性高斯分布。

因此，\(L_{t-1}\)是唯一剩下的损失项，它是正向过程（以\(x_t\)和初始样本\(x_0\)为条件）的“后验”与参数化反向扩散过程之间的KL散度。这两个项也是高斯分布

\[L_{vlb}:=L_{t-1}:=D_{KL}(q(x_{t-1}|x_{t},x_{0})||p_{\theta}(x_{t-1}|x_{t})) \]

术语\(\mathrm{q(x_{t-1}|x_{t},x_{0})}\)被称为“前向过程后向分布”

我们的深度学习模型在训练过程中的工作是近似/估计这个（高斯）后验的参数，使KL散度尽可能小。

Image to illustrate the point why we need to minimize the KL divergence between the forward posterior and the reverse process in denoising diffusion probabilistic models (DDPMs).

后验分布的参数如下：

\[\begin{aligned} q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})& =\mathcal{N}(\mathbf{x}_{t-1};\tilde{\boldsymbol{\mu}}_{t}(\mathbf{x}_{t},\mathbf{x}_{0}),\tilde{\boldsymbol{\beta}}_{t}\mathbf{I}), \\ \mathrm{where}\quad\tilde{\mu}_{t}(\mathbf{x}_{t},\mathbf{x}_{0})& :=\frac{\sqrt{\alpha_{t-1}}\beta_{t}}{1-\bar{\alpha}_{t}}\mathbf{x}_{0}+\frac{\sqrt{\alpha_{t}}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}}\mathbf{x}_{t}\quad\mathrm{and}\quad\tilde{\beta}_{t}:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t} \end{aligned} \]

为了进一步简化模型的任务，作者决定将方差固定为常数\(\beta_t\)。

现在，模型只需要学习预测上述方程。反向扩散核被修改为：

\[p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})=\mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta}(\mathbf{x}_{t},t),\Sigma_{\theta}(\mathbf{x}_{t},t)) \]

\[p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})={\mathcal{N}}(\mathbf{x}_{t-1};\mu_{\theta}(\mathbf{x}_{t},t),\sigma^{2}I) \]

由于我们保持方差恒定，最小化KL散度就像最小化两个高斯分布\(q\)和\(p\)的均值（𝞵）之间的差（或距离）一样简单（例如，左图像中分布均值之间的差），可以按如下方式完成：

\[L_{t-1}=\mathbb{E}_{q}\left[\frac{1}{2\sigma_{t}^{2}}\|\tilde{\mu}_{t}(\mathbf{x}_{t},\mathbf{x}_{0})-\mu_{\theta}(\mathbf{x}_{t},t)\|^{2}\right]+C \]

现在，我们可以采取三种方法：

直接预测\(x_0\)并在后验函数中使用它进行查找\(\tilde{\mu}\)。
预测整个\(\tilde{\mu}\)。
预测每个时间步的噪音。这是通过使用重新参数化技巧将\(\tilde{\mu}\)中\(x_0\)写成\(x_t\)来实现的。\(\mathbf{x}_{t}:=\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\epsilon\)

通过使用第三种选择，经过一些简化，\(\tilde{\mu}\)可以表示为：

\[\tilde{\mu}(x_{t},x_{0})=\frac{1}{\sqrt{\bar{\alpha}_{t}}}\left(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{t}\right) \]

同样，\(\mu_{\theta}(x_{t},t)\)的公式设置为：

\[\mu_\theta(x_t,x_0)=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t,t)\right) \]

在训练和推理时，我们知道\(𝝱\)、\(𝛂\)和\(x_t\)。因此，我们的模型只需要预测每个时间步长的噪声。去噪扩散概率模型中使用的简化（忽略一些加权项后）损失函数如下：

\[L_{\mathrm{simple}}(\theta):=\mathbb{E}_{t,\mathbf{x}_{0},\epsilon}\left[\left\|\epsilon-\epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\boldsymbol{\epsilon},t)\right\|^{2}\right] \]

Comparing just the noise.

这基本上是：

\[L_{\mathrm{simple}}=E_{t,x_0,\epsilon}\left[||\epsilon-\epsilon_\theta(x_t,t)||^2\right] \]

这是我们用来训练DDPM的最终损失函数，它只是正向过程中添加的噪声与模型预测的噪声之间的“均方误差”。这是本文对扩散概率模型去噪的最有影响力的贡献。

这太棒了，因为从那些看起来很可怕的ELBO术语开始，我们最终得到了整个机器学习领域中最简单的损失函数。

4. 在PyTorch中从头开始编写DDPM

从本节开始，我们将在PyTorch中从头开始编写训练去噪扩散概率模型所需的所有基本组件。我们使用Kaggle内核代替Colab，因为它提供了比Colab免费版本更好的GPU和更长的训练时间（这对扩散模型至关重要）。

注意：经常使用的辅助函数的代码不会添加到帖子中。

💡 您可以通过订阅博客文章来访问此文章和我们所有其他文章的整个代码库，我们将向您发送下载链接。

https://github.com/spmallick/learnopencv/tree/master/Guide-to-training-DDPMs-from-Scratch

首先，我们将定义配置类，这些类将包含用于加载数据集、创建日志目录和训练模型的超参数。

from dataclasses import dataclass
 
@dataclass
class BaseConfig:
    DEVICE = get_default_device()
    DATASET = "Flowers"  #  "MNIST", "Cifar-10", "Flowers"
 
    # For logging inferece images and saving checkpoints.
    root_log_dir = os.path.join("Logs_Checkpoints", "Inference")
    root_checkpoint_dir = os.path.join("Logs_Checkpoints", "checkpoints")
 
    # Current log and checkpoint directory.
    log_dir = "version_0"
    checkpoint_dir = "version_0"
 
 
@dataclass
class TrainingConfig:
    TIMESTEPS = 1000  # Define number of diffusion timesteps
    IMG_SHAPE = (1, 32, 32) if BaseConfig.DATASET == "MNIST" else (3, 32, 32)
    NUM_EPOCHS = 800
    BATCH_SIZE = 32
    LR = 2e-4
    NUM_WORKERS = 2

5. 创建PyTorch数据集类对象

本文使用“Flowers”数据集，该数据集可以从Kaggle下载或快速加载到Kaggle内核环境中。但您可能已经注意到，在BaseConfig类中，我们还提供了加载MNIST、Cifare10和Cifare100数据集的选项。你可以选择你喜欢的。

flowers数据集可以从这里下载：Flowers Recognition | Kaggle

使用Kaggle内核时，只需单击“添加数据”组件并选择数据集即可。

在这里，我们创建两个函数：

get_dataset(…)：返回将传递给Dataloader的数据集类对象。对数据集中的每个图像应用三个预处理变换和一个增强。
1. 预处理：
  1. 转换[0, 255]→[0.0, 1.0]范围内的像素值
  2. 根据形状调整图像大小（32x32）。
  3. 从[0.0, 1.0]→[-1.0, 1.0]范围更改像素值。这是由DDPM作者完成的，这样输入图像的值范围与标准高斯图像大致相同。
2. 增强：
  1. 随机水平翻转，如原始实现中使用的。如果你使用的是MNIST数据集，一定要注释掉这一行。
inverse_transfers(…)：此函数用于反转加载步骤中应用的变换，并将图像恢复到[0.0, 255.0]范围。

import torchvision
import torchvision.transforms as TF
import torchvision.datasets as datasets
from torch.utils.data import Dataset, DataLoader
 
 
def get_dataset(dataset_name='MNIST'):
    transforms = torchvision.transforms.Compose(
        [
            torchvision.transforms.ToTensor(),
            torchvision.transforms.Resize((32, 32), 
                                          interpolation=torchvision.transforms.InterpolationMode.BICUBIC, 
                                          antialias=True),
            torchvision.transforms.RandomHorizontalFlip(),
#             torchvision.transforms.Normalize(MEAN, STD),
            torchvision.transforms.Lambda(lambda t: (t * 2) - 1) # Scale between [-1, 1] 
        ]
    )
     
    if dataset_name.upper() == "MNIST":
        dataset = datasets.MNIST(root="data", train=True, download=True, transform=transforms)
    elif dataset_name == "Cifar-10":    
        dataset = datasets.CIFAR10(root="data", train=True, download=True, transform=transforms)
    elif dataset_name == "Cifar-100":
        dataset = datasets.CIFAR10(root="data", train=True, download=True, transform=transforms)
    elif dataset_name == "Flowers":
        dataset = datasets.ImageFolder(root="/kaggle/input/flowers-recognition/flowers", transform=transforms)
 
    return dataset
 
def inverse_transform(tensors):
    """Convert tensors from [-1., 1.] to [0., 255.]"""
    return ((tensors.clamp(-1, 1) + 1.0) / 2.0) * 255.0

6. 创建PyTorch数据加载器类对象

接下来，我们定义get_dataloader(…)函数，该函数返回所选数据集的dataloader对象。

def get_dataloader(dataset_name='MNIST', 
                   batch_size=32, 
                   pin_memory=False, 
                   shuffle=True, 
                   num_workers=0, 
                   device="cpu"
                  ):
    dataset      = get_dataset(dataset_name=dataset_name)
    dataloader = DataLoader(dataset, batch_size=batch_size, 
                            pin_memory=pin_memory, 
                            num_workers=num_workers, 
                            shuffle=shuffle
                           )
    # Used for moving batch of data to the user-specified machine: cpu or gpu
    device_dataloader = DeviceDataLoader(dataloader, device)
    return device_dataloader

7. 可视化数据集

首先，我们将通过调用get_dataloader(…)函数来创建“dataloader”对象。

loader = get_dataloader(
    dataset_name=BaseConfig.DATASET,
    batch_size=128,
    device=”cpu”,
)

然后，我们可以简单地使用torchvision的make_grid(…)函数来绘制花朵图像的网格。

from torchvision.utils import make_grid
 
plt.figure(figsize=(10, 4), facecolor='white')
 
for b_image, _ in loader:
    b_image = inverse_transform(b_image)
    grid_img = make_grid(b_image / 255.0, nrow=16, padding=True, pad_value=1)
    plt.imshow(grid_img.permute(1, 2, 0))
    plt.axis("off")
    break

Flowers Dataset

8. DDPM中使用的模型架构

在DDPM中，作者使用了一个UNet形状的深度神经网络，该网络将以下内容作为输入：

在反向过程的任何阶段输入图像。
输入图像的时间步长。

从通常的UNet架构开始，作者用ResNet模型中使用的“残差块”替换了每个级别的原始双卷积。

该架构由5个组件组成：

编码器块
瓶颈块
解码器块
自注意力模块
正弦位置编码

结构细节：

编码器和解码器路径中有四个级别，它们之间有瓶颈块。
每个编码器级包括两个残差块，除了最后一级之外，其余都进行了卷积下采样。
每个相应的解码器级包括三个残差块，并使用2x最近邻卷积对前一级的输入进行上采样。
编码器路径中的每个阶段都在跳过连接的帮助下连接到解码器路径。
该模型使用单一特征图分辨率的“自我关注”模块。
模型中的每个残差块都从前一层（以及解码器路径中的其他层）获得输入，并嵌入当前时间步长。时间步长嵌入通知模型输入在马尔可夫链中的当前位置。

The U-Net architecture used in DDPMs

在本文中，我们正在研究（32×32）的图像大小。我们的模型和本文中使用的原始模型之间只存在两个微小的变化。

我们使用64个基本通道，而不是128个。
编码器和解码器路径都有四个级别。每个级别的特征图大小保持如下：32→16→8→8。我们在特征图大小为（16x16）和（8x8）时应用自我注意，而不是在原始情况下，它们在特征图尺寸为（16x16）时只应用一次。

请注意，我们没有添加模型代码，因为UNet+的代码很容易修改，但因为所有不同的组件。它变得太大了，无法添加到帖子中。

9. 扩散类

在本节中，我们将创建一个名为SimpleDiffusion的类。此类包含：

执行正向和反向扩散过程所需的调度器常量。
定义DDPM中使用的线性方差调度器的方法。
一种使用更新的前向扩散核执行单个步骤的方法。

class SimpleDiffusion:
    def __init__(
        self,
        num_diffusion_timesteps=1000,
        img_shape=(3, 64, 64),
        device="cpu",
    ):
        self.num_diffusion_timesteps = num_diffusion_timesteps
        self.img_shape = img_shape
        self.device = device
        self.initialize()
 
    def initialize(self):
        # BETAs & ALPHAs required at different places in the Algorithm.
        self.beta  = self.get_betas()
        self.alpha = 1 - self.beta
         
        self_sqrt_beta                       = torch.sqrt(self.beta)
        self.alpha_cumulative                = torch.cumprod(self.alpha, dim=0)
        self.sqrt_alpha_cumulative           = torch.sqrt(self.alpha_cumulative)
        self.one_by_sqrt_alpha               = 1. / torch.sqrt(self.alpha)
        self.sqrt_one_minus_alpha_cumulative = torch.sqrt(1 - self.alpha_cumulative)
          
    def get_betas(self):
        """linear schedule, proposed in original ddpm paper"""
        scale = 1000 / self.num_diffusion_timesteps
        beta_start = scale * 1e-4
        beta_end = scale * 0.02
        return torch.linspace(
            beta_start,
            beta_end,
            self.num_diffusion_timesteps,
            dtype=torch.float32,
            device=self.device,
        )

10. 正向扩散过程的Python代码

在本节中，我们将编写python代码，根据这里提到的方程式在一个步骤中执行“正向扩散过程”。

forward_diffusion(...)函数接收一批图像和相应的时间步长，并使用更新的前向扩散核方程添加噪声/破坏输入图像。

def forward_diffusion(sd: SimpleDiffusion, x0: torch.Tensor, timesteps: torch.Tensor):
    eps = torch.randn_like(x0)  # Noise
    mean    = get(sd.sqrt_alpha_cumulative, t=timesteps) * x0  # Image scaled
    std_dev = get(sd.sqrt_one_minus_alpha_cumulative, t=timesteps) # Noise scaled
    sample  = mean + std_dev * eps # scaled inputs * scaled noise
 
    return sample, eps  # return ... , gt noise --> model predicts this

10.1 样本图像正向扩散过程的可视化

在本节中，我们将可视化一些样本图像的前向扩散过程，看看它们在\(T\)个时间步内通过马尔可夫链时是如何被破坏的。

sd = SimpleDiffusion(num_diffusion_timesteps=TrainingConfig.TIMESTEPS, device="cpu")
 
loader = iter(  # converting dataloader into an iterator for now.
    get_dataloader(
        dataset_name=BaseConfig.DATASET,
        batch_size=6,
        device="cpu",
    )
)

对某些特定时间步执行正向处理，并存储原始图像的噪声版本。

x0s, _ = next(loader)
 
noisy_images = []
specific_timesteps = [0, 10, 50, 100, 150, 200, 250, 300, 400, 600, 800, 999]
 
for timestep in specific_timesteps:
    timestep = torch.as_tensor(timestep, dtype=torch.long)
 
    xts, _ = sd.forward_diffusion(x0s, timestep)
    xts    = inverse_transform(xts) / 255.0
    xts    = make_grid(xts, nrow=1, padding=1)
     
    noisy_images.append(xts)

绘制不同时间步的样本损坏情况。

_, ax = plt.subplots(1, len(noisy_images), figsize=(10, 5), facecolor='white')
 
for i, (timestep, noisy_sample) in enumerate(zip(specific_timesteps, noisy_images)):
    ax[i].imshow(noisy_sample.squeeze(0).permute(1, 2, 0))
    ax[i].set_title(f"t={timestep}", fontsize=8)
    ax[i].axis("off")
    ax[i].grid(False)
 
plt.suptitle("Forward Diffusion Process", y=0.9)
plt.axis("off")
plt.show()

The original image gets increasingly corrupted as timesteps increase. At the end of the forward process, we are left with noise.

11. 用于去噪扩散概率模型的训练和采样算法

基于算法1的训练代码：

这里定义的第一个函数是train_one_epoch(…)。此函数用于执行“一个训练周期”，即它通过在整个数据集上迭代一次来训练模型，并将在我们的最终训练循环中调用。

我们还使用混合精度训练来更快地训练模型并节省GPU内存。代码非常简单，几乎是算法的一对一转换。

# Algorithm 1: Training
 
def train_one_epoch(model, loader, sd, optimizer, scaler, loss_fn, epoch=800, 
                   base_config=BaseConfig(), training_config=TrainingConfig()):
     
    loss_record = MeanMetric()
    model.train()
 
    with tqdm(total=len(loader), dynamic_ncols=True) as tq:
        tq.set_description(f"Train :: Epoch: {epoch}/{training_config.NUM_EPOCHS}")
          
        for x0s, _ in loader: # line 1, 2
            tq.update(1)
             
            ts = torch.randint(low=1, high=training_config.TIMESTEPS, size=(x0s.shape[0],), device=base_config.DEVICE) # line 3
            xts, gt_noise = sd.forward_diffusion(x0s, ts) # line 4
 
            with amp.autocast():
                pred_noise = model(xts, ts)
                loss = loss_fn(gt_noise, pred_noise) # line 5
 
            optimizer.zero_grad(set_to_none=True)
            scaler.scale(loss).backward()
 
            # scaler.unscale_(optimizer)
            # torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
 
            scaler.step(optimizer)
            scaler.update()
 
            loss_value = loss.detach().item()
            loss_record.update(loss_value)
 
            tq.set_postfix_str(s=f"Loss: {loss_value:.4f}")
 
        mean_loss = loss_record.compute().item()
     
        tq.set_postfix_str(s=f"Epoch Loss: {mean_loss:.4f}")
     
    return mean_loss

基于算法2的采样或推理代码：

我们定义的下一个函数是reverse_diffusion(...)，它负责执行推理，即使用反向扩散过程生成图像。该函数接受一个训练好的模型和扩散类，可以生成一个展示整个扩散过程的视频，也可以仅生成最终生成的图像。

# Algorithm 2: Sampling
     
@torch.no_grad()
def reverse_diffusion(model, sd, timesteps=1000, img_shape=(3, 64, 64), 
                      num_images=5, nrow=8, device="cpu", **kwargs):
 
    x = torch.randn((num_images, *img_shape), device=device)
    model.eval()
 
    if kwargs.get("generate_video", False):
        outs = []
 
    for time_step in tqdm(iterable=reversed(range(1, timesteps)), 
                          total=timesteps-1, dynamic_ncols=False, 
                          desc="Sampling :: ", position=0):
 
        ts = torch.ones(num_images, dtype=torch.long, device=device) * time_step
        z = torch.randn_like(x) if time_step > 1 else torch.zeros_like(x)
 
        predicted_noise = model(x, ts)
 
        beta_t                            = get(sd.beta, ts)
        one_by_sqrt_alpha_t               = get(sd.one_by_sqrt_alpha, ts)
        sqrt_one_minus_alpha_cumulative_t = get(sd.sqrt_one_minus_alpha_cumulative, ts) 
 
        x = (
            one_by_sqrt_alpha_t
            * (x - (beta_t / sqrt_one_minus_alpha_cumulative_t) * predicted_noise)
            + torch.sqrt(beta_t) * z
        )
 
        if kwargs.get("generate_video", False):
            x_inv = inverse_transform(x).type(torch.uint8)
            grid = make_grid(x_inv, nrow=nrow, pad_value=255.0).to("cpu")
            ndarr = torch.permute(grid, (1, 2, 0)).numpy()[:, :, ::-1]
            outs.append(ndarr)
 
    if kwargs.get("generate_video", False): # Generate and save video of the entire reverse process. 
        frames2vid(outs, kwargs['save_path'])
        display(Image.fromarray(outs[-1][:, :, ::-1])) # Display the image at the final timestep of the reverse process.
        return None
 
    else: # Display and save the image at the final timestep of the reverse process. 
        x = inverse_transform(x).type(torch.uint8)
        grid = make_grid(x, nrow=nrow, pad_value=255.0).to("cpu")
        pil_image = TF.functional.to_pil_image(grid)
        pil_image.save(kwargs['save_path'], format=save_path[-3:].upper())
        display(pil_image)
        return None

12. 从头开始训练DDPM

在前面的部分中，我们已经定义了训练所需的所有必要类和函数。我们现在要做的就是组装它们并开始训练过程。

在我们开始训练之前：

我们将首先定义所有与模型相关的超参数。
然后初始化UNet模型、AdamW优化器、MSE损失函数和其他必要的类。

@dataclass
class ModelConfig:
    BASE_CH = 64  # 64, 128, 256, 256
    BASE_CH_MULT = (1, 2, 4, 4) # 32, 16, 8, 8 
    APPLY_ATTENTION = (False, True, True, False)
    DROPOUT_RATE = 0.1
    TIME_EMB_MULT = 4 # 128
 
model = UNet(
    input_channels          = TrainingConfig.IMG_SHAPE[0],
    output_channels         = TrainingConfig.IMG_SHAPE[0],
    base_channels           = ModelConfig.BASE_CH,
    base_channels_multiples = ModelConfig.BASE_CH_MULT,
    apply_attention         = ModelConfig.APPLY_ATTENTION,
    dropout_rate            = ModelConfig.DROPOUT_RATE,
    time_multiple           = ModelConfig.TIME_EMB_MULT,
)
model.to(BaseConfig.DEVICE)
 
optimizer = torch.optim.AdamW(model.parameters(), lr=TrainingConfig.LR) # Original → Adam
 
dataloader = get_dataloader(
    dataset_name  = BaseConfig.DATASET,
    batch_size    = TrainingConfig.BATCH_SIZE,
    device        = BaseConfig.DEVICE,
    pin_memory    = True,
    num_workers   = TrainingConfig.NUM_WORKERS,
)
 
loss_fn = nn.MSELoss()
 
sd = SimpleDiffusion(
    num_diffusion_timesteps = TrainingConfig.TIMESTEPS,
    img_shape               = TrainingConfig.IMG_SHAPE,
    device                  = BaseConfig.DEVICE,
)
 
scaler = amp.GradScaler() # For mixed-precision training.

然后，我们将初始化日志记录和检查点目录，以保存中间采样结果和模型参数。

total_epochs = TrainingConfig.NUM_EPOCHS + 1
log_dir, checkpoint_dir = setup_log_directory(config=BaseConfig())
generate_video = False
ext = ".mp4" if generate_gif else ".png"

最后，我们可以编写训练循环。由于我们已经将所有代码划分为简单、易于调试的函数和类，现在我们所要做的就是在epochs训练循环中调用它们。具体来说，我们需要在循环中调用上一节中定义的“训练”和“采样”函数。

for epoch in range(1, total_epochs):
    torch.cuda.empty_cache()
    gc.collect()
     
    # Algorithm 1: Training
    train_one_epoch(model, sd, dataloader, optimizer, scaler, loss_fn, epoch=epoch)
 
    if epoch % 20 == 0:
        save_path = os.path.join(log_dir, f"{epoch}{ext}")
         
        # Algorithm 2: Sampling
        reverse_diffusion(model, sd, timesteps=TrainingConfig.TIMESTEPS, 
                          num_images=32, generate_video=generate_video, save_path=save_path, 
                          img_shape=TrainingConfig.IMG_SHAPE, device=BaseConfig.DEVICE, nrow=4,
        )
 
        # clear_output()
        checkpoint_dict = {
            "opt": optimizer.state_dict(),
            "scaler": scaler.state_dict(),
            "model": model.state_dict()
        }
        torch.save(checkpoint_dict, os.path.join(checkpoint_dir, "ckpt.pt"))
        del checkpoint_dict

如果一切顺利，培训程序应开始并打印培训日志，类似于：

13. 使用DDPM生成图像

如果你对每20个迭代生成的样本感到满意，你可以让训练完成800个迭代，也可以在其间中断。

为了执行推理，我们只需重新加载保存的模型，您可以使用相同或不同的日志目录来保存结果。您也可以重新初始化SimpleDiffusion类，但这不是必需的。

# Reloading model from saved checkpoint
model = UNet(
    input_channels          = TrainingConfig.IMG_SHAPE[0],
    output_channels         = TrainingConfig.IMG_SHAPE[0],
    base_channels           = ModelConfig.BASE_CH,
    base_channels_multiples = ModelConfig.BASE_CH_MULT,
    apply_attention         = ModelConfig.APPLY_ATTENTION,
    dropout_rate            = ModelConfig.DROPOUT_RATE,
    time_multiple           = ModelConfig.TIME_EMB_MULT,
)
model.load_state_dict(torch.load(os.path.join(checkpoint_dir, "ckpt.tar"), map_location='cpu')['model'])
 
model.to(BaseConfig.DEVICE)
 
sd = SimpleDiffusion(
    num_diffusion_timesteps = TrainingConfig.TIMESTEPS,
    img_shape               = TrainingConfig.IMG_SHAPE,
    device                  = BaseConfig.DEVICE,
)
 
log_dir = "inference_results"

推理代码只是使用训练好的模型调用reverse_didiffusion(...) 函数。

generate_video = False # Set it to True for generating video of the entire reverse diffusion proces or False to for saving only the final generated image.
 
ext = ".mp4" if generate_video else ".png"
filename = f"{datetime.now().strftime('%Y%m%d-%H%M%S')}{ext}"
 
save_path = os.path.join(log_dir, filename)
 
reverse_diffusion(
    model,
    sd,
    num_images=256,
    generate_video=generate_video,
    save_path=save_path,
    timesteps=1000,
    img_shape=TrainingConfig.IMG_SHAPE,
    device=BaseConfig.DEVICE,
    nrow=32,
)
print(save_path)

我们得到的一些结果：

14. 总结

总之，扩散模型代表了一个快速增长的领域，为未来带来了丰富的令人兴奋的可能性。随着这一领域的研究不断发展，我们可以期待出现更先进的技术和应用。我鼓励读者分享他们对这一主题的想法和问题，并就扩散模型的未来进行对话。

总结这篇文章📜, 我们涵盖了一系列相关主题。

我们首先为为什么我们需要生成模型这一基本问题提供了直观的答案。
然后，我们继续讨论，从逻辑和理论的角度解释基于扩散的生成模型。
在建立了理论基础后，我们逐一介绍了DDPM推导出的所有必要的数学方程，同时保持了流畅度，使其易于掌握。
最后，我们通过解释从头开始训练DDPM和执行推理所需的所有不同代码来总结。我们还展示了实验结果。

参考目录

我们很乐意收到您的来信。请随时在评论区提问；我们非常乐意与您交谈。

🌟快乐学习！

posted @ 2024-11-09 21:05 张天明阅读(26) 评论(0) 编辑收藏举报

刷新页面返回顶部