【论文阅读】N-BEATS Neural basis expansion analysis for interpretable time series forecasting
原始题目:N-BEATS: Neural basis expansion analysis for interpretable time series forecasting
中文翻译:N-BEATS:可解释时间序列预测的神经基展开分析
发表时间:2020-02-20
平台:arXiv
文章链接:http://arxiv.org/abs/1905.10437
开源代码:https://github.com/servicenow/n-beats
摘要
我们专注于使用深度学习解决单变量时间序列点预测问题。我们提出了一种基于后向和前向残差链路以及完全连接层的深度堆栈的深度神经架构。该体系结构具有许多理想的特性,可解释,无需修改即可应用于广泛的目标域,并且训练速度快。我们在几个著名的数据集上测试了所提出的架构,包括M3、M4和旅游比赛数据集,这些数据集包含来自不同领域的时间序列。我们为所有数据集展示了N-BEATS的两种配置的最先进性能,比统计基准提高了11%的预测精度,比去年的M4竞赛(一种神经网络和统计时间序列模型之间的域调整手工混合)的获胜者提高了3%。我们模型的第一种配置不使用任何时间序列特定的组件,其在异构数据集上的性能强烈表明,与公认的观点相反,深度学习原语(如残差块)本身就足以解决广泛的预测问题。最后,我们展示了如何增强所提出的体系结构,以提供可解释的输出,而不会造成相当大的准确性损失。
1. 引言
时间序列(TS)预测是一个重要的商业问题,也是机器学习(ML)的一个富有成果的应用领域。它是现代商业的大多数方面的基础,包括库存控制和客户管理等关键领域,以及从生产和分销到财务和营销的商业规划。因此,它具有相当大的财务影响,通常每获得一点预测准确性就要花费数百万美元(Jain,2017;Kahn,2003年)。然而,与计算机视觉或自然语言处理等领域不同的是,深度学习(DL)技术现在已经根深蒂固,仍然有证据表明ML和DL难以超越经典的统计TS预测方法(Makridakis等人,2018a;b)。例如,在总共60个参赛作品中,提交给M4竞赛的六种“纯”ML方法的排名分别为23、37、38、48、54和57,大多数最佳排名方法都是经典统计技术的集合(Makridakis等人,2018b)。
另一方面,M4比赛的获胜者(Smyl,2020)是基于神经残差/注意力扩张LSTM堆栈与具有可学习参数的经典Holt-Winters统计模型(Holt,1957;2004;Winters,1960)之间的混合。由于Smyl的方法在很大程度上依赖于Holt-Winters组件,Makridakis等人(2018b)进一步认为,“混合方法和方法组合是提高预测准确性和使预测更有价值的前进方向”。在这项工作中,我们希望通过探索纯DL架构在TS预测中的潜力来挑战这一结论。此外,在可解释的DL架构设计的背景下,我们有兴趣回答以下问题:我们是否可以在模型中注入适当的归纳偏差,使其内部操作更具可解释性,即提取一些可解释的驱动因素,结合起来产生给定的预测?
1.1 贡献总结
深度神经架构:据我们所知,这是第一项实证证明不使用时间序列特定组件的纯DL在M3、M4和旅游数据集上优于公认的统计方法的工作(在M4上,比统计基准高11%,比最佳统计条目高7%,比M4竞赛获胜者高3%)。在我们看来,这为在TS预测中使用纯ML提供了一个长期缺失的概念证明,并加强了继续推进该领域研究的动力。
时间序列的可解释DL:除了准确性优势外,我们还表明,设计一个具有可解释输出的架构是可行的,该架构可以被从业者以与传统分解技术(如“季节性趋势水平”方法)非常相同的方式使用(Cleveland et al.,1990)。
与传统分解技术相当的可解释程度
2. 问题陈述
我们考虑离散时间中的单变量点预测问题。给定一个长度为H的预测范围——一个长度T的观测序列历史[y1,…,yT]∈RT,任务是预测未来值y∈RH=[yT+1,yT+2,…,yT+H]的向量。为了简单起见,我们稍后将考虑以最后一个观测值yT结束的长度为t≤t的回顾窗口作为模型输入,并表示x∈Rt=[yT−t+1,…,yT]。我们将y表示为y的预测。以下指标通常用于评估预测性能(Hyndman&Koehler,2006;Makridakis&Hibon,2000;Makridakis等人,2018b;Athanasopoulos等人,2011):
这里,m是数据的周期性(例如,对于月序列为12)。MAPE(Mean Absolute Percentage Error,平均绝对百分比误差)、sMAPE(symmetric MAPE,对称MAPE)和MASE(Mean-Absolute Scaled Error,平均绝标度误差)是预测实践中的标准无标度度量(Hyndman&Koehler,2006;Makridakis&Hibon,2000):而sMAPE通过预测和地面实况之间的平均值来缩放误差,MASE通过简单地复制过去m个周期测量的观测值的天真预测器的平均误差进行缩放,从而考虑季节性。OWA(总体加权平均值)是一种特定于M4的指标,用于对参赛作品进行排名(M4团队,2018b),其中sMAPE和MASE指标被归一化,使得经季节性调整的天真预测获得OWA=1.0。
3. N-BEATS
我们的架构设计方法依赖于几个关键原则。首先,基础架构应该是简单的、通用的,但具有表现力(深度)。其次,体系结构不应依赖于时间序列特定的功能工程或输入缩放。这些先决条件使我们能够探索纯DL架构在TS预测中的潜力。最后,作为探索可解释性的先决条件,体系结构应该是可扩展的,以使其输出具有人类可解释性。现在,我们将讨论这些原则如何与所提出的体系结构相融合。
3.1基本块
所提出的基本构建块具有分叉结构,如图1(左)所示。在本节中,我们将重点详细描述“第\(l\)-个块”的操作(请注意,为了简洁起见,图1中删除了块索引)。第\(l\)个块接受相应的输入\(x_l\),并输出两个向量,$ \widehat{y_l}\(和\) \widehat{x_l}\(。对于模型中的第一个块,其相应的x是整个模型输入——一个以最后一次测量观测结束的具有一定长度的历史回顾窗口。我们将输入窗口的长度设置为预测范围H的倍数,在我们的设置中,x的典型长度范围从2H到7H。对于其余的块,它们的输入\)x_l\(是先前块的剩余输出。每个块有两个输出:\) \widehat{y_l}\(,块对长度H的前向预测;以及\) \widehat{x_l}\(,块对\)x_l$的最佳估计,也称为“反向预测”,给定块可以用来近似信号的函数空间的约束。
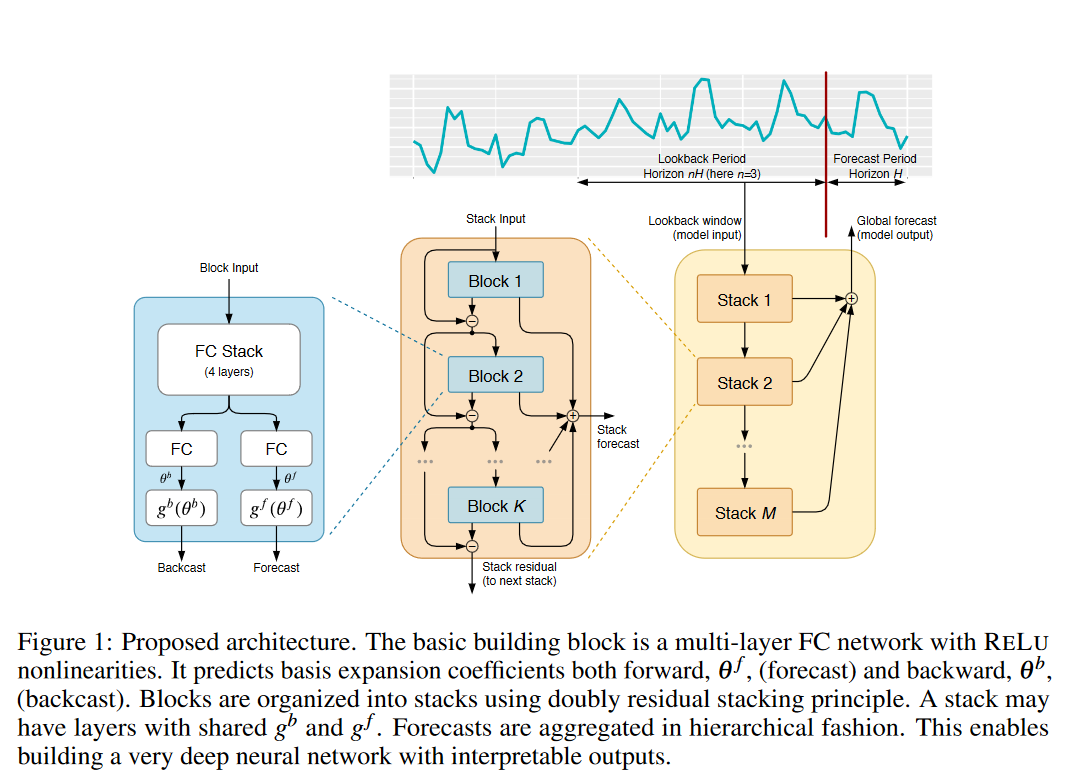
图1:建议的体系结构。基本构建块是具有RELU非线性的多层FC网络。它预测前向基展开系数θf(预测)和后向基展开因数θb(反向)。使用双残差堆叠原理将块组织成堆叠。堆栈可能具有具有共享gb和g f的层。预测是以分层方式聚合的。这使得能够构建具有可解释输出的非常深入的神经网络。
在内部,基本构建块由两部分组成。第一部分是一个完全连接的网络,它产生展开系数的前向θf和后向θb预测因子(再次注意,图1中的\(θ^b_l\)、\(θ^f_l\)、\(g^b_l\)、\(g^f_l\)去掉了块索引)。第二部分由后向\(g^b\)和前向\(g^f\)基层组成,它们接受各自的前向θf和后向θb展开系数,将它们内部投影在基函数集上,并产生前一段中定义的后向x和预测输出y。
第\(l\)块的第一部分的操作由以下方程描述:
这里线性层只是一个线性投影层,即\(\theta_{\ell}^{f}=\mathbf{W}_{\ell}^{f}\mathbf{h}_{\ell,4}\)。FC层是具有RELU非线性的标准全连接层(Nair&Hinton,2010),使得对于\(FC_{l,1}\),例如:\(\theta_{\ell}^{f}=\mathbf{W}_{\ell}^{f}\mathbf{h}_{\ell,4}\)。该架构的这一部分的一个任务是预测前向展开系数θf,最终目标是通过适当混合由g f提供的基向量来优化部分预测\(\widehat{\mathbf{y}}_{\ell}\)的精度。此外,该子网络预测gb使用的向后扩展系数θb来产生x的估计,最终目标是通过去除其输入中对预测没有帮助的分量来帮助下游块。
网络的第二部分通过基层将展开系数θf和θb映射到输出,\(\widehat{\mathbf{y}}_{\ell}=g_{\ell}^{f}(\boldsymbol{\theta}_{\ell}^{f})\)和\(\widehat{\mathbf{x}}_{\ell}=g_{\ell}^{b}(\theta_{\ell}^{b})\)。其操作由以下方程描述:
\(\widehat{\mathbf{y}}_{\ell}=\sum_{i=1}^{\dim(\boldsymbol{\theta}_{\ell}^{f})}\boldsymbol{\theta}_{\ell,i}^{f}\mathbf{v}_{i}^{f},\quad\widehat{\mathbf{x}}_{\ell}=\sum_{i=1}^{\dim(\boldsymbol{\theta}_{\ell}^{b})}\boldsymbol{\theta}_{\ell,i}^{b}\mathbf{v}_{i}^{b}.\)
这里,\(v^f_i\)和\(v^b_i\)是预测和回溯基向量,\(θ^f_{l,i}\)是\(θ^f_l\)的第i个元素。\(g^b_l\)和\(g^f_l\)的函数是提供足够丰富的集合\(\{v^f_ i\}^{dim(θ^f_l)}_{i=1}\)和\(\{v^b_i\}^{dim(θ^b_l)}_{i=1}\),使得它们各自的输出可以通过变化的展开系数\(θ^f_l\)和\(θ^b_l\)来充分表示。如下所示,\(g^b_l\)和\(g^f_l\)可以被选择为可学习的,也可以被设置为特定的函数形式,以反映某些特定于问题的归纳偏差,从而适当地约束输出的结构。第3.3节讨论了\(g^b_l\)和\(g^f_l\)的具体例子。
3.2 双重剩余堆叠
经典的残差网络架构在将结果传递给下一个堆栈之前,将层堆栈的输入添加到其输出中(He et al.,2016)。Huang等人提出的DenseNet架构(2017)通过引入从每个堆栈的输出到后面的每个其他堆栈的输入的额外连接来扩展这一原理。这些方法在提高深度架构的可训练性方面提供了明显的优势。在这项工作的背景下,它们的缺点是导致难以解释的网络结构。我们提出了一种新的分层双残差拓扑,如图1所示(中间和右边)。所提出的架构具有两个残差分支,一个在每层的反向预测上运行,另一个在每个层的预测分支上运行。其操作由以下方程描述:
\(\mathbf{x}_{\ell}=\mathbf{x}_{\ell-1}-\widehat{\mathbf{x}}_{\ell-1},\quad\widehat{\mathbf{y}}=\sum_{\ell}\widehat{\mathbf{y}}_{\ell}.\)
如前所述,在第一个块的特殊情况下,其输入是模型级输入x,\(x_1\equiv x\)。对于所有其他块,可以将反向残差分支\(x_l\)视为对输入信号进行顺序分析。前一个块删除了信号\(\widehat{\mathbf{x}}_{\ell-1}\)中它可以很好地近似的部分,使下游块的预测工作更容易。这种结构还促进了更多的流体梯度反向传播。更重要的是,每个块都输出一个部分预测y,该预测首先在堆栈级别聚合,然后在整个网络级别聚合,从而提供分层分解。最终预测y是所有部分预测的总和。在通用模型上下文中,当允许堆栈对每层具有任意的\(g^b_l\)和\(g^f_l\)时,这使得网络对梯度流更加透明。在一个特殊的情况下,在堆栈上共享的中\(g^b_l\)和\(g^f_l\)强制执行刻意结构,这一点至关重要,即通过聚合有意义的部分预测来实现可解释性。
3.3 可解释性
在选择\(g^b_l\)和\(g^f_l\)的基础上,我们提出了两种体系结构配置。其中一个是通用DL,另一个是用某些可解释的归纳偏差扩充的。
通用体系结构不依赖于TS特定的知识。我们将\(g^b_l\)和\(g^f_l\)设置为前一层输出的线性投影。在这种情况下,块l的输出被描述为:
\(\widehat{\mathbf{y}}_{\ell}=\mathbf{V}_{\ell}^{f}\mathbf{\theta}_{\ell}^{f}+\mathbf{b}_{\ell}^{f},\quad\widehat{\mathbf{x}}_{\ell}=\mathbf{V}_{\ell}^{b}\mathbf{\theta}_{\ell}^{b}+\mathbf{b}_{\ell}^{b}.\)
该模型的解释是,图中所示的基本构建块中的FC层在网络学习的基础\(V^f_l\)中学习部分预测\(\widehat{y}_l\)的预测分解。矩阵\(V^f_l\)具有维度\(H×dim(θ^f_l)\)。因此,\(V^f_l\)的第一维具有预测域中离散时间指数的解释。矩阵的第二个维度解释了基函数的指数,其中\(θ^f_l\)是该基的展开系数。因此,\(V^f_l\)的列可以被认为是时域中的波形。由于没有对\(V^f_l\)的形式施加额外的约束,因此深度模型学习的波形不具有固有结构(在我们的实验中也没有明显的结构)。这导致\(\widehat{y}_l\)不可解释。
可解释的体系结构可以通过重用图1中的整体体系结构方法和在堆栈级别向基础层添加结构来构建。预测从业者通常使用将时间序列分解为趋势性和季节性的方法,例如STL(Cleveland et al.,1990)和X13-ARIMA(美国人口普查局,2013)执行的方法。我们建议将趋势和季节性分解设计到模型中,以使堆栈输出更容易解释。请注意,对于通用模型,堆栈的概念是不必要的,为了清晰起见,省略了堆栈级别的索引。现在我们将同时考虑堆栈级别和块级别的索引。例如,\(\widehat{\mathbf{y}}_{s,\ell}\),将表示堆栈s内块l的部分预测。
趋势模型。趋势的一个典型特征是,大多数时候它是一个单调函数,或者至少是一个缓慢变化的函数。为了模拟这种行为,我们建议将\(g^b_{s,l}\)和\(g^f_{s,l}\)约束为小阶p的多项式,这是一个在预测窗口内缓慢变化的函数:
这里,时间向量\(t=[0,1,2,…,H−2,H−1]^T/H\)定义在从0到(H−1)/H的离散网格上,预测前方H步。或者,矩阵形式的趋势预测将是:
\(\widehat{\mathbf{y}}_{s,\ell}^{tr}=\mathbf{T}\theta_{s,\ell}^{f},\)
其中\(\theta_{s,\ell}^{f}\)是由方程(1)描述的堆栈s的层的FC网络预测的多项式系数;并且T=[1,T,…,tp]是T的幂矩阵。如果p很低,例如2或3,则它迫使\(\hat{\mathbf{y}}_{s,\ell}^{tr}\)模拟趋势。
季节性模型。季节性的典型特征是它是一种有规律的、周期性的、反复出现的波动。因此,为了对季节性进行建模,我们建议将\(g^b_{s,l}\)和\(g^f_{s,l}\)约束为属于周期函数类,即yt=yt-∆,其中∆是季节性周期。对周期函数建模的基础的自然选择是傅立叶级数:
\(\widehat{\mathbf{y}}_{s,\ell}^{seas}=\mathbf{S}\theta_{s,\ell}^{f},\)
其中\(\theta_{s,\ell}^{f}\)是由方程(1)描述的堆栈s的层的FC网络预测的傅立叶系数;\(\mathbf{S}=[\mathbf{1},\cos(2\boldsymbol{\pi}\mathbf{t}),\ldots\cos(2\boldsymbol{\pi}|H/2-1|\mathbf{t})),\sin(2\boldsymbol{\pi}\mathbf{t}),\ldots,\sin(2\boldsymbol{\pi}|H/2-1|\mathbf{t}))]\)。因此,预测的\(\widehat{\mathbf{y}}_{s,\ell}^{seas}\)是一个模仿典型季节模式的周期函数。
整体可解释架构由两个堆栈组成:趋势堆栈后面是季节性堆栈。双残差叠加与预测/反向预测原理相结合导致(i)趋势分量在被馈送到季节性叠加之前从输入窗口x中被去除,以及(ii)趋势和季节性的部分预测可作为单独的可解释输出获得。从结构上讲,每个堆栈由几个用残差连接连接的块组成,如图1所示。每个堆栈共享其各自的不可学习的\(g^b_{s,l}\)和\(g^f_{s,l}\)。对于趋势性和季节性,区块数量均为3。我们发现,除了共享\(g^b_{s,l}\)和\(g^f_{s,l}\)之外,在堆栈中的块之间共享所有权重会带来更好的验证性能。
3.4组装
在M4比赛中,所有顶尖选手都使用Ensembling。我们也依靠组合来进行比较。我们发现,集合是一种比流行的替代方案(如丢弃或L2范数惩罚)更强大的正则化技术。这些方法的加入改进了单个模型,但损害了整体的性能。合奏的核心属性是多样性。我们使用多种多样性来源构建了一个乐团。首先,集合模型适用于三个不同的度量:sMAPE、MASE和MAPE,这是sMAPE的一个版本,在分母中只有基本真值。其次,对于每个地平线H,在不同长度的输入窗口上训练各个模型:2H,3H,7H总共六个窗口长度。因此,整体系综呈现出多尺度方面。最后,我们通过包括用不同随机初始化训练的模型来执行装袋过程(Breiman,1996)。我们总共使用180个模型来报告测试集的结果(关于整体尺寸的消融,请参阅附录B)。我们使用中值作为集合聚合函数。
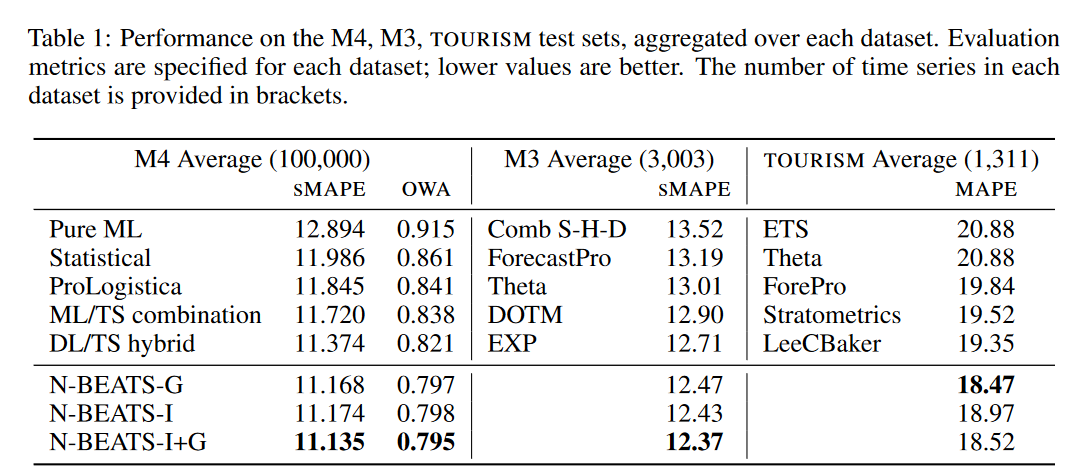
表1:M4、M3、TOURISM测试集的性能,在每个数据集上汇总。为每个数据集指定了评估指标;值越低越好。括号中提供了每个数据集中时间序列的数量。
4. 相关工作
TS预测的方法可以分为几个不同的类别。基于指数平滑及其不同风格的统计建模方法已经建立起来,并且通常被认为是行业中的默认选择(Holt,1957;2004;Winters,1960)。指数平滑的更高级变体包括M3竞争的获胜者,Theta方法(Assimakopoulos&Nikolopoulos,2000),该方法将预测分解为几个θ线,并将它们进行统计组合。统计方法的顶峰包括ARIMA、自动ARIMA和一般的统一状态空间建模方法,可用于解释和分析上述所有方法(概述见Hyndman&Khandakar(2008))。最近,ML/TS组合方法开始渗透到该领域,并取得了巨大成功,通过使用统计引擎的输出作为特征,显示出了有希望的结果。事实上,在M4比赛中排名前五的参赛作品中,有两个是这种类型的方法,包括第二个参赛作品(Montero Manso et al.,2019)。第二个条目计算M4数据集上几种统计方法的输出,并使用梯度增强树将其组合(Chen和Guestrin,2016)。在某种程度上独立地,现代深度学习TS预测的工作是基于递归神经网络的变化发展起来的(Flunkert et al.,2017;Rangapuram et al.,2018b;Toubeau et al.,2019;Zia&Razzaq,2018)在很大程度上被多变量设置中的电力负荷预测所主导。一些早期的工作探索了递归神经网络与扩张、残差连接和注意力的组合(Chang et al.,2017;Kim等人,2017;秦等人,2017)。这些都是M4比赛获胜者的基础(Smyl,2020)。获胜的条目结合了Holt-Winters风格的季节性模型,其参数通过梯度下降和每个预测范围的膨胀/残差/注意力方法的独特组合拟合到给定的TS。由此产生的模型是一个混合模型,在架构上严重依赖于时间序列引擎。它是针对M4的每个特定领域手工制作的,这使得这种方法很难推广到其他数据集。
5. 实验结果
我们基于几个数据集的总体性能指标的关键实证结果——M4(M4团队,2018b;Makridakis等人,2018b)、M3(Makridakis&Hibon,2000;Makridakis等人,2018a)和旅游(Athanasopoulos等人,2011)——如表1所示。第5.1节和附录A提供了数据集的更详细描述。对于每个数据集,我们将我们的结果与文献中报告的该数据集的最佳5个条目进行比较,根据每个数据集特有的习惯指标(M4:OWA和sMAPE,M3:SMAP E,TOURISM:MAPE)。更精细的数据集特定结果以及预测范围和时间序列类型的数据划分出现在各自的附录中(M4:附录C.1;M3:附录C.2;旅游:附录C.3)。
在表1中,我们研究了两种N-BEATS配置的性能:通用的(N-BEATS-G)和可解释的(N-BEATS-I),以及N-BEATS-I+G(来自N-BEATS-G和N-BEATS-I的所有模型的集合)。在M4数据集上,我们与来自M4竞争的5个代表进行了比较(Makri-dakis et al.,2018b):每个代表在各自的模型类别中都是最好的。纯ML是B.Trotta提交的,是6个纯ML模型中最好的一个。统计是N.Z.Legaki和K.Koutsouri的最佳纯统计模型。ML/TS组合是P.Montero-Manso、T.Talagala、R.J.Hyndman和G.Athanasopoulos的模型,在一些统计时间序列模型上排名第二,梯度增强树。ProLogistica是M4中基于统计方法加权集合的第三个条目。最后,DL/TS混合动力是M4比赛的获胜者(Smyl,2020)。在M3数据集上,我们与M3的获胜者Theta方法(Assimakopoulos&Nikolopoulos,2000)进行了比较;DOTA,一种动态优化的Theta模型(Fiorucci等人,2016);EXP,最新的统计方法和之前M3的最先进技术(Spiliotis等人,2019);以及ForecastPro,一种现成的预测软件,基于指数平滑、ARIMA和移动平均之间的模型选择(Athanasopoulos等人,2011;Assimakopoulos和Nikolopoulos,2000年)。在旅游数据集上,我们与3个统计基准进行了比较(Athanasopoulos et al.,2011):ETS,具有交叉验证的加法/乘法模型的指数平滑;Theta方法;ForePro,与M3中的ForecastPro相同;以及旅游Kaggle竞赛的前两名参赛作品(Athanasopoulos&Hyndman,2011):Stratometrics,一种未知的技术;LeeCBaker(Baker&Howard,2011),Naïve、线性趋势模型和指数加权最小二乘回归趋势的加权组合。
根据表1,N-BEATS在三个具有挑战性的非重叠数据集上展示了最先进的性能,这些数据集包含来自非常不同领域的时间序列、采样频率和季节性。例如,在M4数据集上,N-BEATS和M4获胜者之间的OWA差距(0.821−0.795=0.026)大于M4获胜者和第二个条目之间的差距(0.838−0.821=0.017)。通用N-BEATS模型使用尽可能少的先验知识,没有功能工程,没有缩放,也没有可能被认为是TS特定的内部架构组件。因此,表1中的结果使我们得出结论,DL不需要统计方法或手工制作的特征工程和领域知识的支持,就可以在广泛的TS预测任务中表现得非常好。除此之外,所提出的通用架构在三个不同的数据集上表现非常好,优于各种各样的模型,包括对各自数据集的通用和手动构建的模型,其中包括M4的获胜者,该模型在架构上手动调整为M4数据的每个预测范围子集。
5.1数据集
M4(M4团队,2018b;Makridakis等人,2018b)是自1982年以来Spyros-Makridakis组织的一系列有影响力的预测比赛中的最新一场(Makridaki斯等人,1982)。100k系列数据集庞大而多样,由商业、金融和经济预测中经常遇到的数据组成,采样频率从每小时到每年不等。附录A.1中提供了一个汇总统计表,显示了TS特性的广泛可变性。
M3(Makridakis&Hibon,2000)在组成上与M4相似,但总体规模较小(总时间序列为3003,而M4为100k)。附录A.2提供了一个汇总统计表。在过去的20年里,该数据集支持了在设计更优化的统计模型方面的重大努力,例如Theta及其变体(Assimakopoulos&Nikolopoulos,2000;Fiorucci等人,2016;Spiliotis等人,2019)。此外,最近一份基于M3子集的出版物(Makridakis et al.,2018a)提供了ML模型不如经典统计模型的证据。
旅游(Athanasopoulos et al.,2011)数据集是作为Athanasoopoulos和Hyndman(2011)各自举办的Kaggle比赛的一部分发布的。数据包括政府旅游机构(例如澳大利亚旅游局、香港旅游发展局和新西兰旅游局)以及在以往研究中使用过这些数据的学者提供的月度、季度和年度数据。附录A.3中提供了一个汇总统计表。
5.2 训练方法
我们将每个数据集划分为训练、验证和测试子集。测试子集是之前为每个数据集定义的标准测试集(M4 Team,2018a;Makridakis和Hibon,2000;Athanasopoulos等人,2011年)。每个数据集的验证和训练子集是通过在每个时间序列的最后一个地平线的边界分割它们的完整训练集来获得的。我们使用训练和验证子集来调整超参数。一旦确定了超参数,我们就在完整的训练集上训练模型,并在测试集上报告结果。有关块级别的详细超参数设置,请参阅附录D。N-BEATS是在Tensorflow中实现和训练的(Abadi等人,2015)。我们在各个范围内共享网络的参数,因此我们为每个数据集在每个范围内训练一个模型。如果每个时间序列都被解释为一个单独的任务,这可以与多任务学习联系起来,还可以与元学习联系起来(见第6节的讨论),在元学习中,通过对多个任务的学习来正则化神经网络,以提高泛化能力。我们想强调的是,不同层次和数据集的模型重用相同的体系结构。体系结构超参数(宽度、层数、堆栈数量等)在各个层次和数据集中固定为相同的值(见附录D)。事实上,我们可以跨领域重用体系结构甚至超参数,这表明所提出的体系结构设计在不同性质的时间序列中都能很好地推广。在具有48k时间序列的M4 Monthly子集和具有174时间序列的M3 Others子集上成功地训练了相同的体系结构。这是一个比S.Smyl(Makridakis et al.,2018b)的结果更强的结果,后者不得不使用为不同层位手工制作的非常不同的架构。
为了更新一个地平线的网络参数,我们对固定大小为1024的训练批次进行采样。我们从这个范围中选择1024个TS ID,均匀地随机替换。对于每个选定的TS id,我们从紧接在TS的列车部分中的最后一个点之前的长度LH的历史范围中选择一个随机预测点。LH是一个交叉验证的超参数。我们观察到,对于具有大量时间序列的子集,它往往较小,而对于具有较少时间序列的子集,它往往较大。例如,在海量的Yearly、Monthly、Quarterly子集中,M4 LH等于1.5;并且在中等到小的每周、每天、每小时M4 LH的子集等于10。给定一个采样的预测点,我们将其后面的一个水平点设置为目标预测窗口y,并设置长度2H、3H、…之一的点的历史,前面的7H是网络的输入x。我们使用默认设置和初始学习率为0.001的Adam优化器。在依靠sMAPE度量的最小化来优化系综成员的同时,我们停止分母中的梯度流,以使训练在数值上稳定。神经网络训练在提前停止的情况下运行,并在验证集上确定批次数量。根据神经网络设置和硬件,对整个M4数据集的一个集合成员进行基于GPU的训练需要30分钟到2小时。
5.3 可解释性结果
图2研究了所提出的模型在通用配置和可解释配置中的输出。如第3.3节所述,为了使图1中所示的通用架构可解释,我们将第一个堆栈中的gθ约束为多项式(2)的形式,而第二个堆栈具有傅立叶基(3)的形式。此外,我们使用N-BEATS的通用配置的输出作为控制组(图1中所示的30个残差块的通用模型分为两个堆栈),并在图2中并排绘制通用(后缀“-G”)和可解释(后缀“-I”)堆栈输出。通用模型的输出是任意的且不可解释的:趋势性或季节性或两者都存在于两个堆栈的输出中。输出的幅度(峰到峰)通常在第二堆栈的输出处较小。可解释模型的输出表现出不同的特性:趋势输出是单调的且缓慢移动的,季节性输出是有规律的、周期性的且具有反复波动。如果时间序列中存在显著的季节性,则季节性输出的峰峰值显著大于趋势的峰峰值。类似地,当地面实况信号中不存在明显趋势时,趋势输出的峰峰值往往较小。因此,所提出的可解释架构将其预测分解为两个不同的组件。我们的结论是,DL模型的输出可以通过在体系结构中对可感知的电感偏差进行编码来进行解释。表1证实,这不会导致性能下降。
6. 讨论:与元学习的联系
元学习定义了内部学习过程和外部学习过程。内部学习过程被外部学习过程参数化、条件化或以其他方式影响(Bengio等人,1991)。典型的内部学习与外部学习是动物一生中的个体学习与内部学习过程本身在多代个体中的进化。为了了解这两个水平,通常有助于参考两组参数,即在内部学习过程中修改的内部参数(例如突触权重)和仅在外部学习过程中被修改的外部参数或元参数(例如基因)。
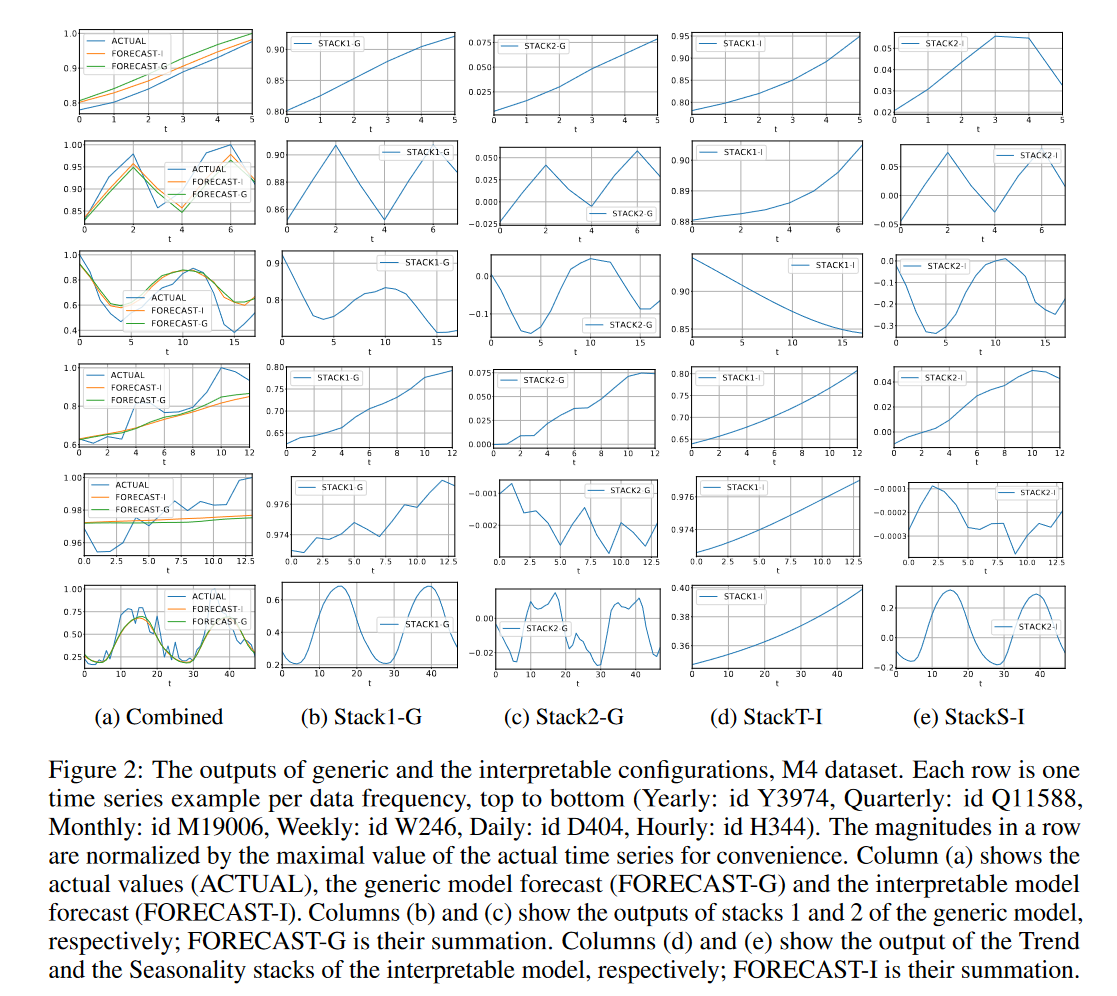
图2:通用和可解释配置的输出,M4数据集。每行是每个数据频率从上到下的一个时间序列示例(年度:id Y3974,季度:id Q11588,月度:id M19006,每周:id W246,每日:id D404,每小时:id H344)。为了方便起见,一行中的幅度通过实际时间序列的最大值进行归一化。列(a)显示了实际值(actual)、通用模型预测(forecast-G)和可解释模型预测(forecast-I)。列(b)和(c)分别示出了通用模型的堆栈1和堆栈2的输出;FORECAST-G是它们的总和。列(d)和(e)分别显示了可解释模型的趋势堆栈和季节堆栈的输出;预测一是他们的总结。
N-BEATS可以通过绘制以下对比图来作为元学习的一个例子。外部学习过程被封装在整个网络的参数中,通过梯度下降进行学习。内部学习过程被封装在一组基本构建块中,并修改基g f作为输入的展开系数θf。内部学习通过一系列阶段进行,每个阶段对应于体系结构堆栈中的一个块。每个块都可以被认为是执行更新步骤的等价物,该更新步骤逐渐修改扩展系数θf,最终将其输入到每个块中的g f中(将其相加以形成最终预测)。内部学习过程从TS中提取一段历史,并将该历史视为一个训练集。它产生前向展开系数θf(见图1),将输入参数映射到预测。此外,每个前一块通过产生后向展开系数θb来修改下一块的输入,从而调节下一个块的学习和输出。在可解释模型的情况下,元参数仅在FC层中,因为g f是固定的。在通用模型的情况下,元参数还包括非参数地定义g f的V。附录B中报告的消融研究结果进一步强化了这一观点,表明增加堆栈中的块数和堆栈数可以提高泛化性能,并可以解释为内部学习过程的更多迭代。
7. 结论
我们提出并实证验证了一种新的单变量TS预测体系结构。我们证明了该体系结构是通用的、灵活的,并且在一系列TS预测问题上表现良好。我们将其应用于三个不重叠的具有挑战性的竞争数据集:M4、M3和TOURISM,并在两种配置中展示了最先进的性能:通用和可解释。这使我们能够验证两个重要的假设:(i)通用DL方法在不使用TS领域知识的情况下对异构单变量TS预测问题表现得非常好,(ii)额外约束DL模型以迫使其将预测分解为不同的人类可解释输出是可行的。我们还证明了DL模型可以在多个时间序列上以多任务的方式进行训练,成功地转移和共享个人学习。我们推测,N-BEATS的表现可以部分归因于它进行了一种形式的元学习,对其进行更深入的研究应该是未来工作的主题。


