二分查找:数的范围
不同于有序数组的简单二分查找,789. 数的范围在更新区间时包含mid,需要考虑边界问题。
1. 题目描述
给定一个按照升序排列的长度为n的整数数组a,返回一个元素k的起始位置和终止位置(位置从0开始计数)。
2. 解题思想
解题思想比较直接,就是分别找到第一个不小于k的元素和最后一个不大于k的元素位置。
3. 二分查找
查找的过程可以使用二分的思想,注意这里与简单的二分查找不同,被称为二分答案。在二分查找中,充分利用a[mid]与k的大小关系,当a[mid] < k时,就到右区间[mid + 1, r]继续查找k;当a[mid] > k时,就到左区间[l, mid - 1]继续查找k;当a[mid] == k或者查找区间长度为0时,查找结束。在二分查找的过程中下一次查找的区间是不包括上一次查找区间的mid的,这种情况下不需要考虑边界问题。
4. 二分答案
在数据范围这道题目中,大小为k的元素有多个,更新区间时包含需要包含mid。下面具体看一下二分答案的两个模板。
模板1
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
模板2
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
前人已经总结出的规律是:
第一个模板是尽量往左找目标,第二个模板是尽量往右找目标。
只要是往左找答案,就用第一个模板,mid不用加一,r=mid,l加一;
只要是往右找答案,就用第二个模板,mid要加一,l=mid,r要减一;
5. 边界问题
二分答案的区间更新根据往左还是往右找目标进行设置,另外还有一个不同点就是mid是不是要加1,而加1与否的区别体现在:往右查找的目标元素在区间右边界的前一个(也就是倒数第二个)和往左查找的目标元素在区间左边界的后一个(也就是正数第二个),在这两种情况下,找到最后的时候,如果mid设置不对,区间长度一直为1,区间保持不变,会陷入死循环。
下面是往右找目标元素3时,mid加1与不加1的过程演示。
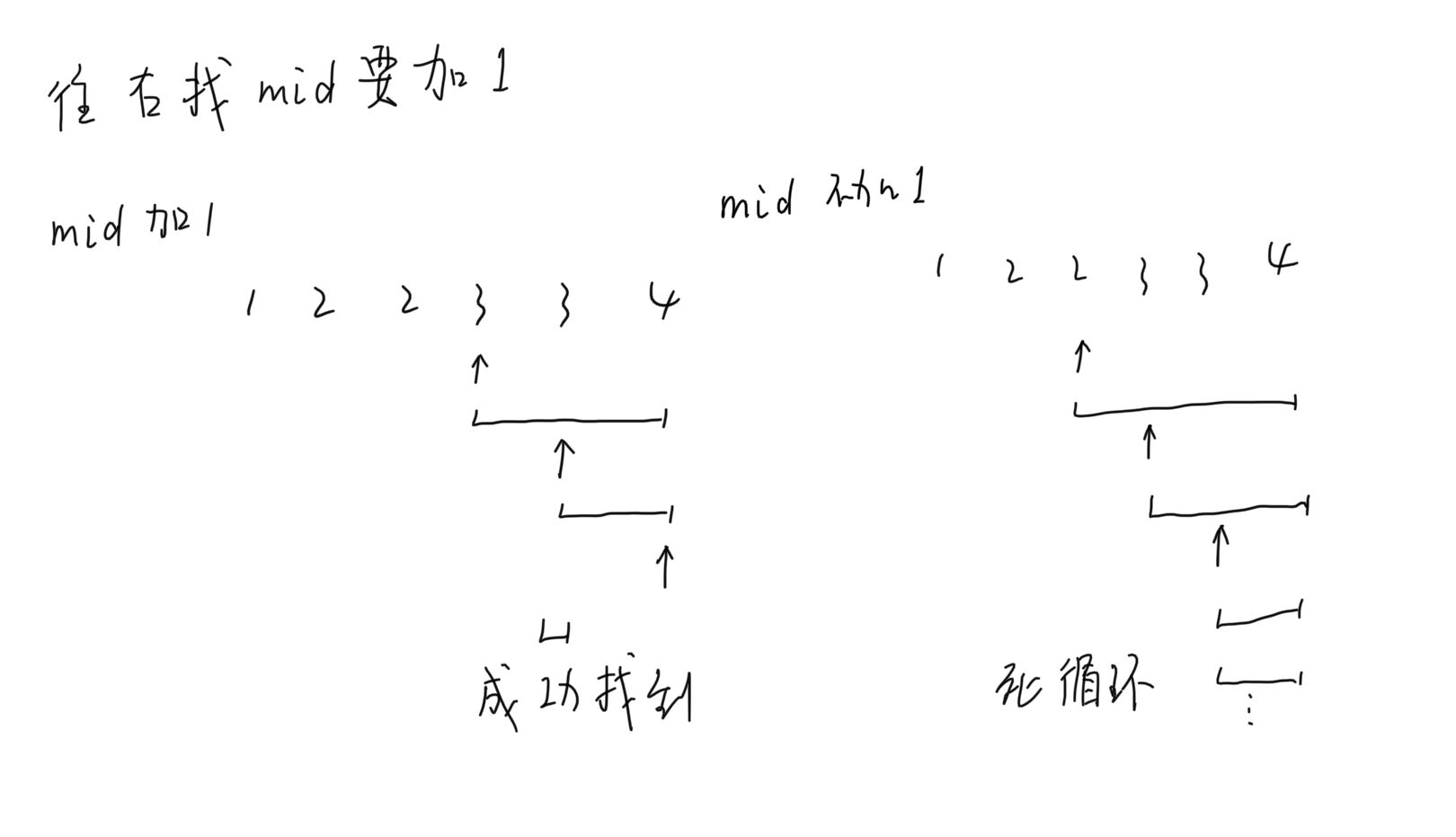
记住往右找加1,往左找不加1,区间更新做题的时候是能很快想出来的。
另外也有人针对如何在最后跳出长度为1的区间死循环,更改循环条件为l+1 != r,也是一种思路,记住一种模板即可。
int L=-1,R=n;
while(L+1!=R)
{
int mid=L+R>>1;
if(check()) L=mid;
else R=mid;
//最后根据你所分左右两边区间的结果
//选取L或者R作为结果
}


