基于TensorFlow和Python的机器学习（笔记4）
基于TensorFlow和Python的机器学习（笔记4）
loss
|
MSE =Mean Squared Error 均方差 |
|
|
Entropy熵 Cross Entropy交叉熵 |
熵越大，越不稳定，惊喜度越高 |
|
|
activation
|
sigmoid |
将每个值映射到0-1范围内 |
 |
|
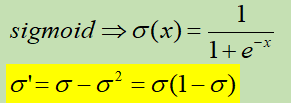softmax |
将每个值映射到0-1范围内，并且，所有值的和为1 小的变得更小，大的变得更大 |
 |
|
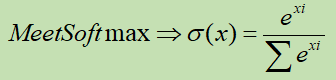tanh |
tanh一般指双曲正切。 tanh是双曲函数中的一个，tanh为双曲正切。在数学中，双曲正切“tanh”是由双曲正弦和双曲余弦这两种基本双曲函数推导而来。 |
 |
|
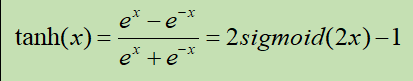Relu |
Rectified Linear Unit整形的线性单元 |
 |
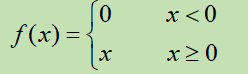矩阵乘法@ 或者matmul
a=tf.constant([[1,2],[3,4]])
# b=[[2],[3]]
# c=a@b
# print(c)
# c=tf.matmul(a,b)
# print(c)
# tf.Tensor(
# [[ 8]
# [18]], shape=(2, 1), dtype=int32)
# tf.Tensor(
# [[ 8]
# [18]], shape=(2, 1), dtype=int32)
#
# 进程已结束,退出代码0
只有元素个数为1的维度，才可以扩张（广播），
不是1个元素的无法在原维度上进行广播
a=tf.random.normal([2,1])
b=tf.broadcast_to(a,[2,4])
print(a)
print(b)
b=tf.broadcast_to(a,[3,2,4])
print(b)
tf.Tensor(
[[ 0.08891886]
[-2.0125113 ]], shape=(2, 1), dtype=float32)
tf.Tensor(
[[ 0.08891886 0.08891886 0.08891886 0.08891886]
[-2.0125113 -2.0125113 -2.0125113 -2.0125113 ]], shape=(2, 4), dtype=float32)
tf.Tensor(
[[[ 0.08891886 0.08891886 0.08891886 0.08891886]
[-2.0125113 -2.0125113 -2.0125113 -2.0125113 ]]
[[ 0.08891886 0.08891886 0.08891886 0.08891886]
[-2.0125113 -2.0125113 -2.0125113 -2.0125113 ]]
[[ 0.08891886 0.08891886 0.08891886 0.08891886]
[-2.0125113 -2.0125113 -2.0125113 -2.0125113 ]]], shape=(3, 2, 4), dtype=float32)
进程已结束,退出代码0
[5]只能扩充（广播）成[n,5]或者[m,n,5]而不能扩充成[5,n]或者 [5,m,n]
广播：只能在前面增加维度，而不能在后面增加维度
a=tf.random.normal([5])
print(a)
# b=tf.broadcast_to(a,[5,2])#Incompatible shapes: [5] vs. [5,2] [Op:BroadcastTo]
# print(b)
b=tf.broadcast_to(a,[2,5])
print(b)
# tf.Tensor([-0.12953417 1.4397062 -0.8788681 -0.1077985 -1.47903 ], shape=(5,), dtype=float32)
# tf.Tensor(
# [[-0.12953417 1.4397062 -0.8788681 -0.1077985 -1.47903 ]
# [-0.12953417 1.4397062 -0.8788681 -0.1077985 -1.47903 ]], shape=(2, 5), dtype=float32)
b=tf.broadcast_to(a,[2,2,5])
print(b)
# tf.Tensor(
# [[[ 0.7871988 1.055641 -0.23075646 -0.7903527 -1.0011079 ]
# [ 0.7871988 1.055641 -0.23075646 -0.7903527 -1.0011079 ]]
#
# [[ 0.7871988 1.055641 -0.23075646 -0.7903527 -1.0011079 ]
# [ 0.7871988 1.055641 -0.23075646 -0.7903527 -1.0011079 ]]], shape=(2, 2, 5), dtype=float32)
Odds（A）= 发生事件A次数 / 其他事件的次数（即不发生A的次数）
请注意Logit一词的分解，对它（it）Log（取对数），这里“it”就是Odds。
矩阵相加时的自动扩张（广播）
import tensorflow as tf
from tensorflow import keras
a=tf.zeros([3,2])
print('a=',a)
b=tf.ones([2,])
print('b=',b)
print('a+b=',a+b)
# a= tf.Tensor(
# [[0. 0.]
# [0. 0.]
# [0. 0.]], shape=(3, 2), dtype=float32)
# b= tf.Tensor([1. 1.], shape=(2,), dtype=float32)
# a+b= tf.Tensor(
# [[1. 1.]
# [1. 1.]
# [1. 1.]], shape=(3, 2), dtype=float32)
#
创建一个简单的全连接网络
import tensorflow as tf
from tensorflow import keras
print(tf.__version__) # 2.10.0
x = tf.random.normal([2, 3])
model = keras.Sequential([
keras.layers.Dense(2, activation='relu'),
keras.layers.Dense(2, activation='relu'),
keras.layers.Dense(2)
])
model.build(input_shape=[None,3])
# Model: "sequential"
# _________________________________________________________________
# Layer(type)
# Output
# Shape
# Param #
# == == == == == == == == == == == == == == == == == == == == == == == == == == == == == == == == =
# dense(Dense)(None, 2)
# 8
#
# dense_1(Dense)(None, 2)
# 6
#
# dense_2(Dense)(None, 2)
# 6
#
# == == == == == == == == == == == == == == == == == == == == == == == == == == == == == == == == =
# Total
# params: 20
# Trainable
# params: 20
# Non - trainable
# params: 0
两个矩阵可以相乘的条件是啥？
- 矩阵只有当左边矩阵的列数等于右边矩阵的行数时,它们才可以相乘；
- 乘积矩阵的行数等于左边矩阵的行数,乘积矩阵的列数等于右边矩阵的列数；
- 乘积矩阵的元素是左行乘右列再求和
|
RNN |
RNN一般指循环神经网络。 循环神经网络（Recurrent Neural Network, RNN）是一类以序列（sequence）数据为输入，在序列的演进方向进行递归（recursion）且所有节点（循环单元）按链式连接的递归神经网络（recursive neural network）。
|
|
GRNN |
门控循环神经网络（gated recurrent neural network）是为了更好地捕捉时序数据中间隔较大的依赖关系,
|
|
GRU |
门控循环单元（gated recurrent unit, GRU)是一种常用的门控循环神经网络 |
|
BiGRU |
BiGRU 是由单向的、方向相反的、输出由这两个 GRU 的状态共同决定的 GRU 组成的神经网络模型。 |
|
BiGRU-Attention |
BiGRU-Attention 模型共分为三部分：文本向量化输入层、 隐含层和输出层。其中，隐含层由 BiGRU 层、attention 层和 Dense 层（全连接层）三层构成。 |
