基于TensorFlow和Python的机器学习(笔记1)
基于TensorFlow和Python的机器学习(笔记1)

Keras和TensorFlow比较
|
项目 |
Keras |
TensorFlow |
|
学习难度 |
简单 |
困难 |
|
使用弹性 |
中等 |
高 |
|
开发效率 |
高 |
中等 |
|
执行性能 |
高 |
高 |
|
适合用户 |
初学者 |
老油条 |
|
张量运算 |
不用自行设计 |
需要自行设计 |
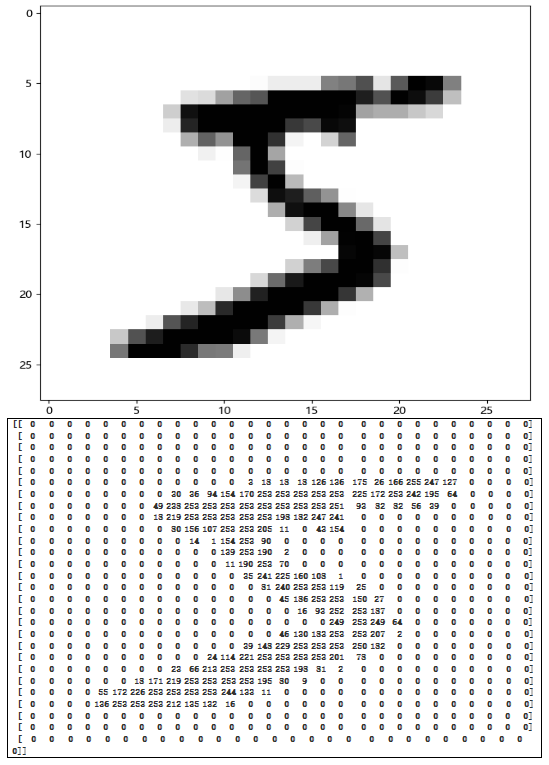
数据图片和矩阵表示对照图(来源MNIST数据集 第一个元素)
模型概述summary
|
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 256) 200960
dense_1 (Dense) (None, 10) 2570
================================================================= Total params: 203,530 Trainable params: 203,530 Non-trainable params: 0 _________________________________________________________________ None |
神经网络参数(可训练)量计算公式

数据集
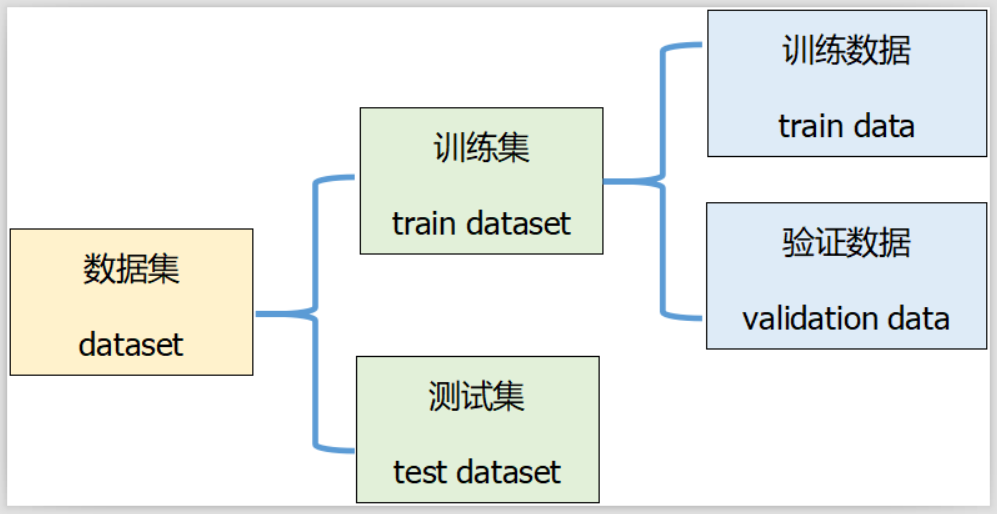
强化学习和深度学习
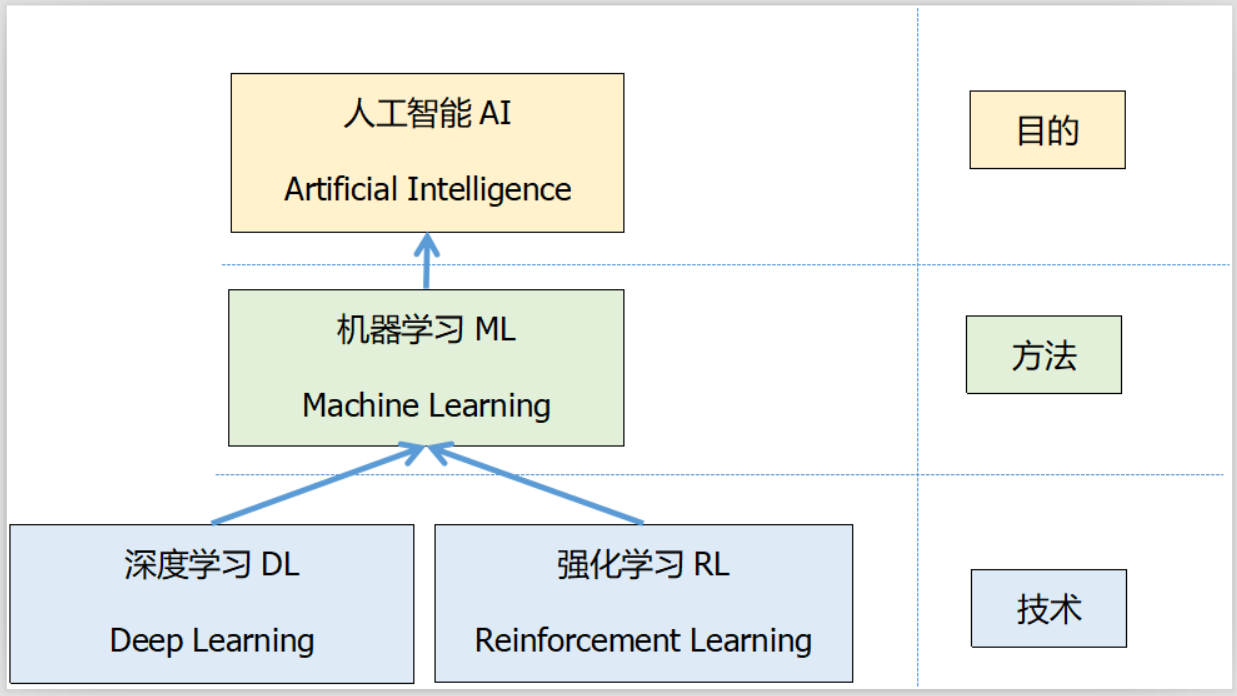
keras 和 tf.keras
|
keras |
tf.keras |
|
作为独立工具,就称为 Keras |
作为 TensorFlow 的一个高阶 API,就称为 tf.keras |
|
keras是API规范,它描述了深度学习框架应如何实现与模型定义和培训相关的特定部分。与框架无关,并支持不同的后端(Theano,Tensorflow等) |
tf.keras是Keras API规范的Tensorflow特定实现。它为该框架增加了对许多Tensorflow特定功能的支持,例如:对tf.data.Dataset作为输入对象的完美支持,对急切执行的支持 |
|
from keras.models import Sequential from keras.models import load_model
|
from tensorflow.keras.models import Sequential from tensorflow.keras.models import load_model
|
|
from keras.layers.pooling import MaxPooling2D |
from tensorflow.keras.layers import MaxPooling2D |
|
fc = keras.layers.Dense(64, activation='relu')
|
fc = tf.keras.layers.Dense(64, activation='relu') |

基本概念
|
池化层 |
Pooling Layer |
用一个数代表一个感受野中的很多数 可以减少参数量 最大池化Max Pooling:池中的最大值代表该池子 平均池化Average Pooling:池中的平均值代表该池子 |
|
激活函数 |
Activation functions |
给神经元引入了非线性因素 使模型可以适配非线性模型 |
|
感受野 |
receptive field |
视觉感受的一个范围; 数据矩阵中的一部分; |
|
交叉熵 |
Cross Entropy |
用来描述语言模型的性能 用来描述模型对文本识别的难度 |
|
卷积 |
convolution |
卷积的“卷”是指翻转平移操作,“积”是指积分运算 采用权值相乘累加的方式提取特征信息 |
|
过拟合 |
Overfitting |
模型在训练集上面表现较好,但是在未见的样本上表现不佳 也就是模型泛化能力偏弱,这种现象叫作过拟合 |
|
欠拟合 |
Underfitting |
训练集上表现不佳,同时在未见的样本上表现也不佳 模型不能够很好地学习到训练集数据的模态,这种现象叫作欠拟合 |
过拟合
|
泛化能力 |
机器学习的主要目的是从训练集上学习到数据的真实模型, 从而能够在未见过的测试 |
|
数据增强 |
除了上述介绍的方式可以有效检测和抑制过拟合现象之外,增加数据集规模是解决过 |
|
表达能力 |
前面已经提到了模型的表达能力,也称之为模型的容量(Capacity)。当模型的表达能力 |
|
容量 |
通俗地讲,模型的容量或表达能力,是指模型拟合复杂函数的能力。 一种体现模型容 |
|
过拟合 Overfitting 欠拟合 Underfitting |
当模型的容量过大时,网络模型除了学习到训练集数据的模态之外,还把额外的观测 |
|
防止过拟合 |
提前终止训练、稀疏化参数、添加正则项、减小网络层数、减小每层的参数量、 增加数据规模(数据增强)、 |
|
|
|
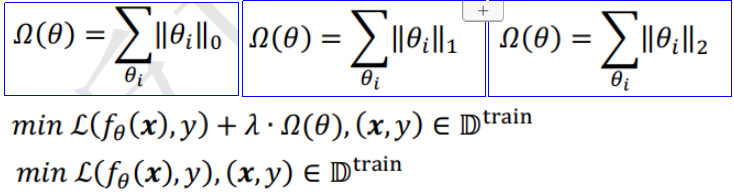
正则化=范数=稀疏性惩罚项
|
L0正则化/范数 |
所有非零元素个数 |
不可导 |
用的不多 |
|
L1正则化/范数 |
所有元素绝对值之和 |
连续可导 |
使用广泛 |
|
L2正则化/范数 |
所有元素平方和 |
连续可导 |
使用广泛 |
|
|
|
|
validation英 [ˌvælɪˈdeɪʃn] 美 [ˌvælɪˈdeɪʃn]
- 验证;确认,批准,生效;肯定,认可确认 验证 校验
batch英 [bætʃ] 美 [bætʃ]n. 一批,一批生产量v. 分批处理
sparse_categorical_accuracy=稀疏-绝对-精确性
sparse_categorical_crossentropy=稀疏-绝对-交叉-熵 函数
accuracy英 [ˈækjərəsi] 美 [ˈækjərəsi]
- 准确性,精确性;准确,精确准确度 准确 准确性
entropy英 [ˈentrəpi] 美 [ˈentrəpi]
- [热] 熵(热力学函数)熵 信息熵 平均信息量
cross-entropy 交叉熵 互熵
categorical英 [ˌkætəˈɡɒrɪk(ə)l] 美 [ˌkætəˈɡɔːrɪk(ə)l]
adj. 绝对的(名词categoricalness,副词categorically,异体字categoric);直截了当的;无条件的;属于某一范畴的 分类的 绝对的 无条件的
sparse英 [spɑːs] 美 [spɑːrs]
adj. 稀少的,稀疏的;简朴的 稀少的 稀疏的 创建稀疏矩阵
iris英 [ˈaɪrɪs] 美 [ˈaɪrɪs]n. 鸢[yuān]尾,鸢[yuān]尾属植物

shuffle英 [ˈʃʌf(ə)l] 美 [ˈʃʌf(ə)l] 打乱
- 将(纸张等)变换位置,打乱顺序;洗(牌);匆忙地整理(或浏览);随机播放;
Sequential英 [sɪˈkwenʃ(ə)l] 美 [sɪˈkwenʃ(ə)l] 存放模型的容器
adj. 连续的,按顺序的;依次发生的,相继发生的;(主计算机)顺序的
Dense英 [dens] 美 [dens] 全连接层
adj. 稠密的;浓密的,浓重的;密度大的;
optimizer英 [ˈɒptɪmaɪzə]n. [计] 优化程序;最优控制器
activation英 [ˌæktɪˈveɪʃn] 美 [ˌæktɪˈveɪʃn] 激活函数
- [电子][物] 激活;活化作用
regularizer正则化矩阵 正则化项 正则项
基本概念
|
L0范数
|
L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0。这太直观了,太露骨了吧,换句话说,让参数W是稀疏的。OK,看到了"稀疏"二字,大家都应该从当下风风火火的"压缩感知"和"稀疏编码"中醒悟过来,原来用的漫山遍野的"稀疏"就是通过这玩意来实现的。但你又开始怀疑了,是这样吗?看到的papers世界中,稀疏不是都通过L1范数来实现吗?脑海里是不是到处都是||W||1影子呀!几乎是抬头不见低头见。没错,这就是这节的题目把L0和L1放在一起的原因,因为他们有着某种不寻常的关系。那我们再来看看L1范数是什么?它为什么可以实现稀疏?为什么大家都用L1范数去实现稀疏,而不是L0范数呢?
|
|
L1范数 |
L1范数是指向量中各个元素绝对值之和,也有个美称叫"稀疏规则算子"(Lasso regularization)。现在我们来分析下这个价值一个亿的问题:为什么L1范数会使权值稀疏?有人可能会这样给你回答"它是L0范数的最优凸近似"。实际上,还存在一个更美的回答:任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个"求和"的形式,那么这个规则化算子就可以实现稀疏。这说是这么说,W的L1范数是绝对值,|w|在w=0处是不可微,但这还是不够直观。这里因为我们需要和L2范数进行对比分析。所以关于L1范数的直观理解,请待会看看第二节。 |
|
L2范数
|
除了L1范数,还有一种更受宠幸的规则化范数是L2范数: ||W||2。它也不逊于L1范数,它有两个美称,在回归里面,有人把有它的回归叫"岭回归"(Ridge Regression),有人也叫它"权值衰减weight decay"。这用的很多吧,因为它的强大功效是改善机器学习里面一个非常重要的问题:过拟合。至于过拟合是什么,上面也解释了,就是模型训练时候的误差很小,但在测试的时候误差很大,也就是我们的模型复杂到可以拟合到我们的所有训练样本了,但在实际预测新的样本的时候,糟糕的一塌糊涂。通俗的讲就是应试能力很强,实际应用能力很差。擅长背诵知识,却不懂得灵活利用知识。 |
|
核范数
|
核范数||W||*是指矩阵奇异值的和,英文称呼叫Nuclear Norm。这个相对于上面火热的L1和L2来说,可能大家就会陌生点。那它是干嘛用的呢?霸气登场:约束Low-Rank(低秩)。 |
|
正则化 |
正则化(regularization),是指在线性代数理论中,不适定问题通常是由一组线性代数方程定义的,而且这组方程组通常来源于有着很大的条件数的不适定反问题。大条件数意味着舍入误差或其它误差会严重地影响问题的结果。 中文名正则化外文名regularization出 处线性代数理论用 途求解不适定问题
|
|
不适定问题 |
经典的数学物理方程定解问题中,人们只研究适定问题。适定问题是指定解满足下面三个要求的问题:① 解是存在的;② 解是唯一的;③ 解连续依赖于定解条件,即解是稳定的。这三个要求中,只要有一个不满足,则称之为不适定问题。 中文名不适定问题外文名ill-posed problem相对概念适定问题属 性数学物理方程定解问题示 例拉普拉斯方程的柯西问题适用领域地球物理、连续介质力学等定 义不满足解是存在的、唯一的、稳定的 |
|
监督机器 |
监督机器学习问题无非就是"minimizeyour error while regularizing your parameters",也就是在规则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据,而规则化参数是防止我们的模型过分拟合我们的训练数据。多么简约的哲学啊!因为参数太多,会导致我们的模型复杂度上升,容易过拟合,也就是我们的训练误差会很小。但训练误差小并不是我们的最终目标,我们的目标是希望模型的测试误差小,也就是能准确的预测新的样本。所以,我们需要保证模型"简单"的基础上最小化训练误差,这样得到的参数才具有好的泛化性能(也就是测试误差也小),而模型"简单"就是通过规则函数来实现的。另外,规则项的使用还可以约束我们的模型的特性。这样就可以将人对这个模型的先验知识融入到模型的学习当中,强行地让学习到的模型具有人想要的特性,例如稀疏、低秩、平滑等等。要知道,有时候人的先验是非常重要的。前人的经验会让你少走很多弯路,这就是为什么我们平时学习最好找个大牛带带的原因。一句点拨可以为我们拨开眼前乌云,还我们一片晴空万里,醍醐灌顶。对机器学习也是一样,如果被我们人稍微点拨一下,它肯定能更快的学习相应的任务。只是由于人和机器的交流目前还没有那么直接的方法,目前这个媒介只能由规则项来担当了。 还有几种角度来看待规则化的。规则化符合奥卡姆剃刀(Occam's razor)原理。这名字好霸气,razor!不过它的思想很平易近人:在所有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。从贝叶斯估计的角度来看,规则化项对应于模型的先验概率。民间还有个说法就是,规则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或惩罚项(penalty term)。 |
|
范数
|
范数(norm)是数学中的一种基本概念。在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即①非负性;②齐次性;③三角不等式。它常常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。 范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。 定义范数的矢量空间是赋范矢量空间;同样,定义半范数的矢量空间就是赋半范矢量空间。 注:在二维的欧氏几何空间 R中定义欧氏范数,在该矢量空间中,元素被画成一个从原点出发的带有箭头的有向线段,每一个矢量的有向线段的长度即为该矢量的欧氏范数。
|
|
泛函
|
泛函就是定义域是一个函数集,而值域是实数集或者实数集的一个子集,推广开来, 泛函就是从任意的向量空间到标量的映射。也就是说,它是从函数空间到数域的映射。 设{y}是给定的函数集,如果对于这个函数集中任一函数y(x) 恒有某个确定的数与之对应,记为П(y(x)),则П(y(x))是定义于集合{y(x)}上的一个泛函。 泛函定义域内的函数为可取函数或容许函数, y(x) 称为泛函П的变量函数。 泛函П(y(x))与可取函数y(x)有明确的对应关系。泛函的值是由一条可取曲线的整体性质决定的。 泛函也是一种“函数”,它的独立变量一般不是通常函数的“自变量”,而是通常函数本身。泛函是函数的函数。由于函数的值是由自变量的选取而确定的,而泛函的值是由自变量函数确定的,故也可以将其理解为函数的函数 泛函的自变量是函数,泛函的自变量称为宗量。 简言之,泛函就是函数的函数。 |
用TensorFlow API:tf.Keras搭建网络八股
|
1 |
import |
导入依赖包 |
|
2 |
datasets |
train(x_train、y_train) test |
|
3 |
class MyModel(Model) model=Mymodel() |
创建模型类 并实例化对象 |
|
4 |
model.compile |
拼装 |
|
5 |
model.fit |
训练 |
|
6 |
model.summary |
描述 |
举例
|
1 |
import |
import tensorflow as tf #创建模型 from sklearn import datasets #数据集来源 import numpy as np #计算库 |
|
2 |
datasets 下载数据集 |
x_train = datasets.load_iris().data #下载数据 y_train = datasets.load_iris().target #下载标签
seed = 116 #种子 np.random.seed(seed) #设置种子 np.random.shuffle(x_train) #打乱数据 np.random.seed(seed) #设置种子 np.random.shuffle(y_train) #打乱数据 tf.random.set_seed(seed) |
|
3 |
model 创建模型 |
model = tf.keras.Sequential([ #用Sequential容器创建模型 tf.keras.layers.Dense(3, #全连接层 activation=tf.keras.activations.softmax, #激活函数 kernel_regularizer=tf.keras.regularizers.l2) #正则化器 ]) |
|
4 |
compile 装配模型 |
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.1), #优化器SGD 学习率0.1 #损失函数 loss=tf.keras.losses.sparse_categorical_crossentropy(from_logits=False), metrics=['sparse_categorical_accuracy'] ) |
|
5 |
fit 训练模型 |
model.fit(x_train, y_train, batch_size=32, epochs=500, validation_split=0.2, validation_freq=20) #输入数据x_train和标签y_train #批次大小32 一般取2的幂 #训练次数500次 |
|
6 |
summary 模型概述 |
model.summary() |
密集向量和稀疏向量的区别: 密集向量的值就是一个普通的Double数组 而稀疏向量由两个并列的 数组indices和values组成 例如:向量(1.0,0.0,1.0,3.0)用密集格式表示为[1.0,0.0,1.0,3.0],用稀疏格式表示为(4,[0,2,3],[1.0,1.0,3.0]) 第一个4表示向量的长度(元素个数),[0,2,3]就是indices数组,[1.0,1.0,3.0]是values数组 表示向量0的位置的值是1.0,2的位置的值是1.0,而3的位置的值是3.0,其他的位置都是0
中文名稀疏向量表示方法通常用两部分表示:一部分是顺序向量,另一部分是值向量
稀疏向量 [1] 通常用两部分表示:一部分是顺序向量,另一部分是值向量。例如稀疏向量(4,0,28,53,0,0,4,8)可用值向量(4,28,53,4,8)和顺序向量(1,0,1,1,0,0,1,1)表示。
scikit-learn Machine Learning in Python
scikit-learn 是一个 Python 的机器学习项目。是一个简单高效的数据挖掘和数据分析工具。基于 NumPy、SciPy 和 matplotlib 构建。
Gitee指数为27,超过42%的开源项目
软件类型:机器学习/深度...|授权协议:BSD|开发语言:Python
简单有效的工具进行预测数据分析
每个人都可以访问,并且可以在各种情况下重用
基于NumPy,SciPy和matplotlib构建
开源,可商业使用-BSD许可证
姓名判男女,基于统计和规则
|
path=r'C:\Users\Administrator\Desktop\name.txt' f=open(path,mode='r',encoding='utf-8') lines=f.readlines() dic=dict() for line in lines: name,sex= line.split('\t') name=name[1:] for zi in name: if zi in dic:#字典中已经存在该键 if '男' in sex: dic[zi]+=1 else : dic[zi] -= 1 else:#字典不存在该键 if '男' in sex: dic[zi] = 1 else: dic[zi] = -1
print(len(dic))
test_path=r'C:\Users\Administrator\Desktop\testname.txt' ff=open(test_path,mode='r',encoding='utf-8') test=ff.readlines() print(len(test)) for name in test: name=name.replace('\n','') if len(name)==3: name2=name[1:] elif len(name)==4: name2=name[2:]
score=0 for zi in name2: if zi in dic: score+=dic[zi] sex='男' if score>0 else '女' print(f'name= {name} ,sex= {sex},score= {score}\n')
name= 龚尧莞 ,sex= 女,score= -25
name= 齐新燕 ,sex= 女,score= -121
name= 车少飞 ,sex= 男,score= 1038
name= 龙家铸 ,sex= 男,score= 1770
name= 赖鸿华 ,sex= 男,score= 2228
name= 龙宣霖 ,sex= 男,score= 805
name= 连丽英 ,sex= 女,score= -1120
name= 齐晓巍 ,sex= 男,score= 351
name= 连俊勤 ,sex= 男,score= 2408
name= 齐明星 ,sex= 男,score= 2784
name= 黄相杰 ,sex= 男,score= 2019
name= 龚小虎 ,sex= 男,score= 499
name= 连传杰 ,sex= 男,score= 2273
name= 宇文献花 ,sex= 女,score= -83
name= 龙川凤 ,sex= 男,score= 60
name= 黄益泉 ,sex= 男,score= 434
name= 黄益波 ,sex= 男,score= 705
name= 米培燕 ,sex= 女,score= -366
name= 连保健 ,sex= 男,score= 652
name= 齐旺梅 ,sex= 女,score= -205
进程已结束,退出代码0
|
N-Gram 语言模型
- Gram是大词汇连续语音识别中常用的一种语言模型,
对中文而言,我们称之为汉语语言模型(CLM, Chinese Language Model)。汉语语言模型利用上下文中相邻词间的搭配信息,可以实现到汉字的自动转换,
中文名汉语语言模型外文名N-Gram定 义计算出具有最大概率的句子
汉语语言模型利用上下文中相邻词间的搭配信息,在需要把连续无空格的拼音、笔划,或代表字母或笔划的数字,转换成汉字串(即句子)时,可以计算出具有最大概率的句子,从而实现到汉字的自动转换,无需用户手动选择,避开了许多汉字对应一个相同的拼音(或笔划串,或数字串)的重码问题。
该模型基于这样一种假设,第N个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。
常用的是二元的Bi-Gram和三元的Tri-Gram。


深度学习(英语:deep learning),是一个多层神经网络是一种机器学习方法。在深度学习出现之前,由于诸如局部最优解和梯度消失之类的技术问题,没有对具有四层或更多层的深度神经网络进行充分的训练,并且其性能也不佳。但是,近年来,Hinton等人通过研究多层神经网络,提高学习所需的计算机功能以及通过Web的开发促进培训数据的采购,使充分学习成为可能。结果,它显示出高性能,压倒了其他方法,解决了与语音,图像和自然语言有关的问题,并在2010年代流行。

机器学习(Machine Learning,ML)是人工智能的子领域,也是人工智能的核心。它囊括了几乎所有对世界影响最大的方法(包括深度学习)。机器学习理论主要是设计和分析一些让计算机可以自动学习的算法。
机器学习和深度学习的区别
|
区别 |
深度学习 |
机器学习 |
|
特征提取 |
自动提取 |
手工设计 |
|
应用场景 |
深度学习主要应用于文字识别、人脸技术、语义分析、智能监控等领域。目前在智能硬件、教育、医疗等行业也在快速布局。 |
机器学习在指纹识别、特征物体检测等领域的应用基本达到了商业化的要求 |
|
数据依赖 |
如果数据量迅速增加,那么深度学习的效果将更加突出,这是因为深度学习算法需要大量数据才能完美理解。 |
机器学习能够适应各种数据量,特别是数据量较小的场景。 |
|
性能 |
当数据量很少的时候,深度学习的性能并不好,因为深度学习算法需要大量数据才能很好理解其中蕴含的模式。 |
|
|
执行时间 |
,由于深度学习中含有非常多的参数,较机器学习而言会耗费更多的时间。 |
机器学习在训练数据的时候费时较少,同时只需几秒到几小时。 |
|
特征1
|
深度学习与传统模式识别方法的最大不同在于它所采用的特征是从大数据中自动学习得到,而非采用手工设计。好的特征可以提高模式识别系统的性能。 |
过去几十年,在模式识别的各种应用中,手工设计的特征一直处于统治地位。手工设计主要依靠设计者的先验知识,很难利用大数据的优势。由于依赖手工调参数,因此特征的设计中所允许出现的参数数量十分有限。深度学习可以从大数据中自动学习特征的表示,可以包含成千上万的参数。 |
|
特征2 |
采用手工设计出有效的特征往往需要五到十年时间,而深度学习可以针对新的应用从训练数据中很快学习到新的有效的特征表示。
|
一个模式识别系统包括特征和分类器两部分。在传统方法中,特征和分类器的优化是分开的。而在神经网络的框架下,特征表示和分类器是联合优化的,可以最大程度地发挥二者联合协作的性能。 |
|
解决问题的方法
|
深度学习则以集中方式解决问题,而不必进行问题拆分。 |
机器学习算法遵循标准程序以解决问题。它将问题拆分成数个部分,对其进行分别解决,而后再将结果结合起来以获得所需的答案。 |
|
结构层次 |
深度学习模型的“深”字意味着神经网络的结构深,由很多层组成。而支持向量机和Boosting等其他常用的机器学习模型都是浅层结构。三层神经网络模型(包括输入层、输出层和一个隐含层)可以近似任何分类函数。既然如此,为什么需要深层模型呢? 研究表明,针对特定的任务,如果模型的深度不够,其所需要的计算单元会呈指数增加。这意味着虽然浅层模型可以表达相同的分类函数,但其需要的参数和训练样本要多得多。 |
浅层模型提供的是局部表达。它将高维图像空间分成若干个局部区域,每个局部区域至少存储一个从训练数据中获得的模板,如图1(a)所示。浅层模型将一个测试样本和这些模板逐一匹配,根据匹配的结果预测其类别。随着分类问题复杂度的增加,需要将图像空间划分成越来越多的局部区域,因而需要越来越多的参数和训练样本。尽管目前许多深度模型的参数量已经相当巨大,但如果换成浅层神经网络,其所需要的参数量要大出多个数量级才能达到相同的数据拟合效果,以至于很难实现。 |
张量运算
|
矩阵乘法 |
tf.matmul=matrix multiply 函数:tf.matmul 表示:将矩阵 a 乘以矩阵 b,生成a * b
numpy.matmul=matrix multiply 原型:numpy.matmul(a,b,out=None)两个numpy数组的矩阵相乘 (1)如果两个参数a,b都是2维的,做普通的矩阵相乘。 (2)如果某个参数是N(N>2)维的,该参数被理解为一些矩阵的stack,计算时会相应的广播。 首先对于a,它会被理解成为两个2*4的矩阵的stack。 对于b,它会被理解成为两个4*2的矩阵的stack。
a=tf.random.uniform([4,3,28,32]) b=tf.random.uniform([4,3,32,22]) c=a@b print(c)#shape=(4, 3, 28, 22)
a=tf.random.uniform([4,3]) b=tf.random.uniform([3,7]) c=a@b print(c)#shape=(4, 7) #a的列数必须等于b的行数,否则报错Matrix size-incompatible #相乘之后的结果是a的行数和b的列数的矩阵;
a=tf.random.uniform([4,3,22]) b=tf.random.uniform([22,7]) c=a@b#shape=(4, 3, 7) print(c)#broadcast自动扩展b为[4,22,7]然后再相乘
# 独热码OneHot y_onehot = tf.one_hot(3, 10) # 共10个分类(元素),下标3的元素(第4个元素)值为1,其余为0 print(y_onehot) # tf.Tensor([0. 0. 0. 1. 0. 0. 0. 0. 0. 0.], shape=(10,), dtype=float32)
|
|
平均值 |
tf.reduce_mean()函数用于计算张量tensor沿着指定的数轴(tensor的某一维度)上的平均值,主要用作降维或者计算tensor(图像)的平均值。 tf.reduce_mean( input_tensor, axis=None, keep_dims=False, name=None, reduction_indices=None ) 参数: input_tensor: 输入的待降维的tensor axis: 指定的轴,如果不指定,则计算所有元素的均值 keep_dims:是否降维度,默认False。设置为True,输出的结果保持输入tensor的形状,设置为False,输出结果会降低维度;如果输入是二维,输出也是二维,维度不变 name: 操作的名称 reduction_indices:在以前版本中用来指定轴,已弃用 类似函数还有: tf.reduce_sum :计算tensor指定轴方向上的所有元素的累加和; tf.reduce_max : 计算tensor指定轴方向上的各个元素的最大值; tf.reduce_all : 计算tensor指定轴方向上的各个元素的逻辑和(and运算); tf.reduce_any: 计算tensor指定轴方向上的各个元素的逻辑或(or运算);
import tensorflow as tf
x = [[1, 2, 3], [4, 5, 6]] # 二维列表 print(type(x)) # <class 'list'> print(x) # [[1, 2, 3], [4, 5, 6]] y=tf.cast(x,dtype=tf.float32)#将二维列表转换为张量 #默认keepdims=False 输出结果降维 mean_all=tf.reduce_mean(y)#所有元素平均值 print(mean_all)#tf.Tensor(3.5, shape=(), dtype=float32) mean_0=tf.reduce_mean(y,axis=0)#同一列上元素求平均 print(mean_0)#tf.Tensor([2.5 3.5 4.5], shape=(3,), dtype=float32) mean_1=tf.reduce_mean(y,axis=1)#同一行上元素求平均 print(mean_1)#tf.Tensor([2. 5.], shape=(2,), dtype=float32) #keepdims=True输出结果维度与输入维度相同 mean_all=tf.reduce_mean(y,keepdims=True) print(mean_all)#tf.Tensor([[3.5]], shape=(1, 1), dtype=float32) mean_0=tf.reduce_mean(y,axis=0,keepdims=True) print(mean_0)#tf.Tensor([[2.5 3.5 4.5]], shape=(1, 3), dtype=float32) mean_1=tf.reduce_mean(y,axis=1,keepdims=True) print(mean_1)#tf.Tensor([[2.] [5.]], shape=(2, 1), dtype=float32) |
|
求导 |
tf.GradientTape梯度带/胶带/磁带 定义在tensorflow/python/eager/backprop.py文件中,从文件路径也可以大概看出,GradientTape是eager模式下计算梯度用的,而eager模式(eager模式的具体介绍请参考文末链接)是TensorFlow 2.0的默认模式,因此tf.GradientTape是官方大力推荐的用法。下面就来具体介绍GradientTape的原理和使用。 Tape在英文中是胶带,磁带的含义,用在这里是由于eager模式带来的影响。在TensorFlow 1.x静态图时代,我们知道每个静态图都有两部分,一部分是前向图,另一部分是反向图。反向图就是用来计算梯度的,用在整个训练过程中。而TensorFlow 2.0默认是eager模式,每行代码顺序执行,没有了构建图的过程(也取消了control_dependency的用法)。但也不能每行都计算一下梯度吧?计算量太大,也没必要。因此,需要一个上下文管理器(context manager)来连接需要计算梯度的函数和变量,方便求解同时也提升效率。
默认情况下GradientTape的资源在调用gradient函数后就被释放,再次调用就无法计算了。所以如果需要多次计算梯度,需要开启persistent=True属性 WARNING:tensorflow:Calling GradientTape.gradient on a persistent tape inside its context is significantly less efficient than calling it outside the context (it causes the gradient ops to be recorded on the tape, leading to increased CPU and memory usage). Only call GradientTape.gradient inside the context if you actually want to trace the gradient in order to compute higher order derivatives. 警告:tensorflow:调用GradientTape。在其上下文中对持久磁带进行梯度操作的效率比在上下文中调用梯度操作的效率要低得多(它导致梯度操作被记录在磁带上,导致CPU和内存使用增加)。 在一个持久胶带(persistent GradientTape)外面求导,效率更高; 一般在网络中使用时,不需要显式调用watch函数,使用默认设置,GradientTape会监控可训练变量;
import tensorflow as tf
x=tf.constant(3.) print(x)#tf.Tensor(3.0, shape=(), dtype=float32) #用GradientTape梯度带 求导数 with tf.GradientTape() as g:
g.watch(x)#看着点X, y = x * x#y=x^2 dy_dx=g.gradient(y,x)# y’ = 2*x = 2*3 = 6 print(dy_dx) # # 例子中的watch函数把需要计算梯度的变量x加进来了。 # GradientTape默认只监控由tf.Variable创建的traiable=True属性(默认)的变量。 # 上面例子中的x是constant,因此计算梯度需要增加g.watch(x)函数。 # 当然,也可以设置不自动监控可训练变量,完全由自己指定, # 设置watch_accessed_variables=False就行了(一般用不到)。
#GradientTape也可以嵌套多层用来计算高阶导数
x=tf.constant(3.) with tf.GradientTape() as g: g.watch(x) with tf.GradientTape()as gg:#嵌套 梯度带 gg.watch(x)#看着点X y=x*x*x #y=x^3 dy_dx=gg.gradient(y,x)#y'=3*x^2=3*3^2=27 print(dy_dx)#tf.Tensor(27.0, shape=(), dtype=float32) d2y_dx2=g.gradient(dy_dx,x)#y''=(3*x^2)'=3*2*x=6*x=18 print(d2y_dx2)#tf.Tensor(18.0, shape=(), dtype=float32)
# 默认情况下GradientTape的资源在调用gradient函数后就被释放,再次调用就无法计算了。 # 所以如果需要多次计算梯度,需要开启persistent=True属性 #RuntimeError: A non-persistent GradientTape can only be used # to compute one set of gradients (or jacobians) #RuntimeError:一个非持久的GradientTape只能用于计算一组梯度(或雅可比矩阵)
x=tf.constant(3.) #持久性胶带,粘得更牢 with tf.GradientTape(persistent=True) as g: g.watch(x) y=x*x#y=x^2, z=y*y#z=y^2=x^4 dy_dx=g.gradient(y,x)#y'=2*x=2*3=6 print(dy_dx)#tf.Tensor(6.0, shape=(), dtype=float32) dz_dx=g.gradient(z,x)#z'=4*x^3=4*27=108 print(dz_dx)#tf.Tensor(108.0, shape=(), dtype=float32) del g #持久性胶带,用完后要删除,非降解材料,不会自动消失
|
张量和变量的区别(Tensor和Variable)
|
tf.Tensor不需计算梯度 tf.Variable需计算梯度 l 为了区分需要计算梯度信息的张量与不需要计算梯度信息的张量,TensorFlow 增加了一种专门的数据类型来支持梯度信息的记录:tf.Variable。 l tf.Variable 类型在普通的张量类型基础上添加了name,trainable 等属性来支持计算图的构建。 l 由于梯度运算会消耗大量的计算资源,而且会自动更新相关参数,对于不需要的优化的张量,如神经网络的输入,不需要通过 tf.Variable 封装; l 相反,对于需要计算梯度并优化的张量, 如神经网络层的W和b, 需要通过 tf.Variable 包裹以便 TensorFlow 跟踪相关梯度信息
import tensorflow as tf
t = tf.constant([1, 2, 3]) # 创建常量张量 v = tf.Variable(t) # 将张量转换为变量Variable(待优化张量、可变张量) print(t) # tf.Tensor([1 2 3], shape=(3,), dtype=int32) print(v) # <tf.Variable 'Variable:0' shape=(3,) dtype=int32, numpy=array([1, 2, 3])> print(v.name) # Variable:0 Variable特有属性 print(v.trainable) # True Variable特有属性 v = tf.Variable([[1, 2], [3, 4]]) # 直接创建Variable张量 print(v) # <tf.Variable 'Variable:0' shape=(2, 2) dtype=int32, numpy=array([[1, 2],[3, 4]])>
ls = [11, 22, 33] # 创建list列表 print(type(ls)) # <class 'list'> t = tf.convert_to_tensor(ls) # 将列表转换为张量 print(t) # tf.Tensor([11 22 33], shape=(3,), dtype=int32)
import numpy as np
arr = np.array([[6.6, 7.7], [100, 200]])#创建一个numpy数组ndarray print(type(arr)) # <class 'numpy.ndarray'> t = tf.convert_to_tensor(arr)#将ndarray转换为张量 print(t) # tf.Tensor([[ 6.6 7.7] [100. 200. ]], shape=(2, 2), dtype=float64)
t=tf.range(5) print(t)#tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int32) |




关键词
|
compile 装配
|
Dense 全连接层
|
|
fit 训练 |
ReLU 激活函数层 |
张量运算
|
矩阵乘法 |
tf.matmul=matrix multiply 函数:tf.matmul 表示:将矩阵 a 乘以矩阵 b,生成a * b
numpy.matmul=matrix multiply 原型:numpy.matmul(a,b,out=None)两个numpy数组的矩阵相乘 (1)如果两个参数a,b都是2维的,做普通的矩阵相乘。 (2)如果某个参数是N(N>2)维的,该参数被理解为一些矩阵的stack,计算时会相应的广播。 首先对于a,它会被理解成为两个2*4的矩阵的stack。 对于b,它会被理解成为两个4*2的矩阵的stack。
a=tf.random.uniform([4,3,28,32]) b=tf.random.uniform([4,3,32,22]) c=a@b print(c)#shape=(4, 3, 28, 22)
a=tf.random.uniform([4,3]) b=tf.random.uniform([3,7]) c=a@b print(c)#shape=(4, 7) #a的列数必须等于b的行数,否则报错Matrix size-incompatible #相乘之后的结果是a的行数和b的列数的矩阵;
a=tf.random.uniform([4,3,22]) b=tf.random.uniform([22,7]) c=a@b#shape=(4, 3, 7) print(c)#broadcast自动扩展b为[4,22,7]然后再相乘
# 独热码OneHot y_onehot = tf.one_hot(3, 10) # 共10个分类(元素),下标3的元素(第4个元素)值为1,其余为0 print(y_onehot) # tf.Tensor([0. 0. 0. 1. 0. 0. 0. 0. 0. 0.], shape=(10,), dtype=float32)
|
|
平均值 |
tf.reduce_mean()函数用于计算张量tensor沿着指定的数轴(tensor的某一维度)上的平均值,主要用作降维或者计算tensor(图像)的平均值。 tf.reduce_mean( input_tensor, axis=None, keep_dims=False, name=None, reduction_indices=None ) 参数: input_tensor: 输入的待降维的tensor axis: 指定的轴,如果不指定,则计算所有元素的均值 keep_dims:是否降维度,默认False。设置为True,输出的结果保持输入tensor的形状,设置为False,输出结果会降低维度;如果输入是二维,输出也是二维,维度不变 name: 操作的名称 reduction_indices:在以前版本中用来指定轴,已弃用 类似函数还有: tf.reduce_sum :计算tensor指定轴方向上的所有元素的累加和; tf.reduce_max : 计算tensor指定轴方向上的各个元素的最大值; tf.reduce_all : 计算tensor指定轴方向上的各个元素的逻辑和(and运算); tf.reduce_any: 计算tensor指定轴方向上的各个元素的逻辑或(or运算);
import tensorflow as tf
x = [[1, 2, 3], [4, 5, 6]] # 二维列表 print(type(x)) # <class 'list'> print(x) # [[1, 2, 3], [4, 5, 6]] y=tf.cast(x,dtype=tf.float32)#将二维列表转换为张量 #默认keepdims=False 输出结果降维 mean_all=tf.reduce_mean(y)#所有元素平均值 print(mean_all)#tf.Tensor(3.5, shape=(), dtype=float32) mean_0=tf.reduce_mean(y,axis=0)#同一列上元素求平均 print(mean_0)#tf.Tensor([2.5 3.5 4.5], shape=(3,), dtype=float32) mean_1=tf.reduce_mean(y,axis=1)#同一行上元素求平均 print(mean_1)#tf.Tensor([2. 5.], shape=(2,), dtype=float32) #keepdims=True输出结果维度与输入维度相同 mean_all=tf.reduce_mean(y,keepdims=True) print(mean_all)#tf.Tensor([[3.5]], shape=(1, 1), dtype=float32) mean_0=tf.reduce_mean(y,axis=0,keepdims=True) print(mean_0)#tf.Tensor([[2.5 3.5 4.5]], shape=(1, 3), dtype=float32) mean_1=tf.reduce_mean(y,axis=1,keepdims=True) print(mean_1)#tf.Tensor([[2.] [5.]], shape=(2, 1), dtype=float32) |
|
求导 |
tf.GradientTape梯度带/胶带/磁带 定义在tensorflow/python/eager/backprop.py文件中,从文件路径也可以大概看出,GradientTape是eager模式下计算梯度用的,而eager模式(eager模式的具体介绍请参考文末链接)是TensorFlow 2.0的默认模式,因此tf.GradientTape是官方大力推荐的用法。下面就来具体介绍GradientTape的原理和使用。 Tape在英文中是胶带,磁带的含义,用在这里是由于eager模式带来的影响。在TensorFlow 1.x静态图时代,我们知道每个静态图都有两部分,一部分是前向图,另一部分是反向图。反向图就是用来计算梯度的,用在整个训练过程中。而TensorFlow 2.0默认是eager模式,每行代码顺序执行,没有了构建图的过程(也取消了control_dependency的用法)。但也不能每行都计算一下梯度吧?计算量太大,也没必要。因此,需要一个上下文管理器(context manager)来连接需要计算梯度的函数和变量,方便求解同时也提升效率。
默认情况下GradientTape的资源在调用gradient函数后就被释放,再次调用就无法计算了。所以如果需要多次计算梯度,需要开启persistent=True属性 WARNING:tensorflow:Calling GradientTape.gradient on a persistent tape inside its context is significantly less efficient than calling it outside the context (it causes the gradient ops to be recorded on the tape, leading to increased CPU and memory usage). Only call GradientTape.gradient inside the context if you actually want to trace the gradient in order to compute higher order derivatives. 警告:tensorflow:调用GradientTape。在其上下文中对持久磁带进行梯度操作的效率比在上下文中调用梯度操作的效率要低得多(它导致梯度操作被记录在磁带上,导致CPU和内存使用增加)。 在一个持久胶带(persistent GradientTape)外面求导,效率更高; 最后,一般在网络中使用时,不需要显式调用watch函数,使用默认设置,GradientTape会监控可训练变量;
import tensorflow as tf
x=tf.constant(3.) print(x)#tf.Tensor(3.0, shape=(), dtype=float32) #用GradientTape梯度带 求导数 with tf.GradientTape() as g:
g.watch(x)#看着点X, y = x * x#y=x^2 dy_dx=g.gradient(y,x)# y’ = 2*x = 2*3 = 6 print(dy_dx) # # 例子中的watch函数把需要计算梯度的变量x加进来了。 # GradientTape默认只监控由tf.Variable创建的traiable=True属性(默认)的变量。 # 上面例子中的x是constant,因此计算梯度需要增加g.watch(x)函数。 # 当然,也可以设置不自动监控可训练变量,完全由自己指定, # 设置watch_accessed_variables=False就行了(一般用不到)。
#GradientTape也可以嵌套多层用来计算高阶导数
x=tf.constant(3.) with tf.GradientTape() as g: g.watch(x) with tf.GradientTape()as gg:#嵌套 梯度带 gg.watch(x)#看着点X y=x*x*x #y=x^3 dy_dx=gg.gradient(y,x)#y'=3*x^2=3*3^2=27 print(dy_dx)#tf.Tensor(27.0, shape=(), dtype=float32) d2y_dx2=g.gradient(dy_dx,x)#y''=(3*x^2)'=3*2*x=6*x=18 print(d2y_dx2)#tf.Tensor(18.0, shape=(), dtype=float32)
# 默认情况下GradientTape的资源在调用gradient函数后就被释放,再次调用就无法计算了。 # 所以如果需要多次计算梯度,需要开启persistent=True属性 #RuntimeError: A non-persistent GradientTape can only be used # to compute one set of gradients (or jacobians) #RuntimeError:一个非持久的GradientTape只能用于计算一组梯度(或雅可比矩阵)
x=tf.constant(3.) #持久性胶带,粘得更牢 with tf.GradientTape(persistent=True) as g: g.watch(x) y=x*x#y=x^2, z=y*y#z=y^2=x^4 dy_dx=g.gradient(y,x)#y'=2*x=2*3=6 print(dy_dx)#tf.Tensor(6.0, shape=(), dtype=float32) dz_dx=g.gradient(z,x)#z'=4*x^3=4*27=108 print(dz_dx)#tf.Tensor(108.0, shape=(), dtype=float32) del g #持久性胶带,用完后要删除,非降解材料,不会自动消失
|

第一个机器学习demo
|
import keras import numpy as np model=keras.Sequential([keras.layers.Dense(units=1,input_shape=[1])]) model.compile(optimizer='sgd',loss='mean_squared_error') #输入x(训练集) xs=np.array([-1.0,0.0,1.0,2.0,3.0,4.0],dtype=float) #标签y ys=np.array([-3.0,-1.0,1.0,3.0,5.0,7.0],dtype=float) #讲数据输入,开始训练,共训练500遍 model.fit(xs,ys,epochs=500) print(f'当x为10.0时,y的预测值为') print(model.predict([10.0])) print(f'当x为-3.0时,y的预测值为') print(model.predict([-3.0]))
''' Epoch 1/500 1/1 [==============================] - 0s 291ms/step - loss: 28.4334 Epoch 2/500 1/1 [==============================] - 0s 999us/step - loss: 22.6760 Epoch 3/500 1/1 [==============================] - 0s 999us/step - loss: 18.1401 Epoch 4/500 1/1 [==============================] - 0s 1000us/step - loss: 14.5652 Epoch 5/500 1/1 [==============================] - 0s 996us/step - loss: 11.7467 Epoch 6/500 1/1 [==============================] - 0s 1ms/step - loss: 9.5233 Epoch 7/500 1/1 [==============================] - 0s 998us/step - loss: 7.7683 Epoch 8/500 1/1 [==============================] - 0s 998us/step - loss: 6.3818 Epoch 9/500 1/1 [==============================] - 0s 1ms/step - loss: 5.2855 Epoch 10/500 1/1 [==============================] - 0s 999us/step - loss: 4.4175
1/1 [==============================] - 0s 1000us/step - loss: 5.2602e-05 Epoch 499/500 1/1 [==============================] - 0s 999us/step - loss: 5.1522e-05 Epoch 500/500 1/1 [==============================] - 0s 1ms/step - loss: 5.0463e-05 当x为10.0时,y的预测值为 1/1 [==============================] - 0s 87ms/step [[18.986246]] 当x为-3.0时,y的预测值为 1/1 [==============================] - 0s 33ms/step [[-6.98784]] '''
|
张量
|
import numpy import tensorflow as tf
t = tf.ones([2, 3]) print(t) # 2行3列的张量,每个元素都是1 t = tf.zeros([3, 4]) print(t) # 3行4列的张量,每个元素都是0 t = tf.fill([3, 6], 99) print(t) # 3行6列的张量,每个元素都是99 t = tf.zeros_like(t) print(t) # 形状同t,行数列数都相同,每个元素都是0 t = tf.ones_like(t) print(t) # 形状同t,行数列数都相同,每个元素都是1 t = tf.one_hot(3, 4) # 共4个元素,下标3的元素为1,其余为0 print(t) # 独热码tf.Tensor([0. 0. 0. 1.], shape=(4,), dtype=float32) t = tf.constant([[1, 2, 3], [9, 8, 7]]) print(t) # tf.Tensor([[1 2 3] [9 8 7]], shape=(2, 3), dtype=int32) # 定义常数张量,指定数据的张量 t = tf.linspace(start=0.0, stop=3.0, num=6) print(t) # tf.Tensor([0. 0.6 1.2 1.8000001 2.4 3.], shape=(6,), dtype=float32) # 等距切分张量,0-0.6-1.2-1.8-2.4-3.0,以0为起始元素,以3为结束元素,等分成6份 t = tf.range(start=0, limit=5, delta=1) print(t) # tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int32) # 指定区间为[0,5)前闭后开,相邻元素差值为1 t = tf.range(start=0.5, limit=2, delta=0.3) print(t) # tf.Tensor([0.5 0.8 1.1 1.4000001 1.7 ], shape=(5,), dtype=float32) # 指定区间[0.5,2),相邻元素差值0.3(步距) t = tf.random.uniform([3, 4], minval=0, maxval=2) print(t)#随机值下限为0上限为2的均匀分布,3行4列 print(numpy.mean(t)) #0.8071537 t = tf.random.normal([3, 4], mean=10, stddev=1) print(t)#均值为10 标准差为1的正态分布,3行4列 print(numpy.mean(t))#9.724729 t=tf.random.truncated_normal([3,4],mean=2,stddev=1) print(t)#均值为2,标准差为1的 截断正态分布,3行4列 print(numpy.mean(t))#2.0792353
''' 截断正态分布的定义可以分为两步,给定一个参数为μ和σ2 的标准正态分布的概率密度函数。修标准般正态分布相关的概率密度函数,通过将范围外的值设置为零,并标准正态的取值范围均匀缩放到特定范围中,使总积分为1。截断范围可以分为四种情况: (1)无截断的情况:− ∞ = a , b = + ∞; (2)下界截断的情况:− ∞ < a , b = + ∞; (3)上界截断的情况:− ∞ = a , b < + ∞; (4)上下界截断的情况:− ∞ < a , b < + ∞;
''' |
TensorFlow的安装
进入python.exe的所在文件夹下输入 (file==>settings==>python intepreter查看所用python解释器的位置)
在命令行窗口中 cd C:\Users\Administrator\venv\Scripts 切换至Python解释器安装路径
pip install tensorflow -i https://pypi.tuna.tsinghua.edu.cn/simple
也可通过
pip install tensorflow==2.5.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
指定tensorflow的版本
Python和TensorFlow版本对应关系
经过测试的构建配置
CPU
版本 Python 版本 编译器 构建工具
tensorflow-2.6.0 3.6-3.9 MSVC 2019 Bazel 3.7.2
tensorflow-2.5.0 3.6-3.9 MSVC 2019 Bazel 3.7.2
tensorflow-2.4.0 3.6-3.8 MSVC 2019 Bazel 3.1.0
tensorflow-2.3.0 3.5-3.8 MSVC 2019 Bazel 3.1.0
tensorflow-2.2.0 3.5-3.8 MSVC 2019 Bazel 2.0.0
tensorflow-2.1.0 3.5-3.7 MSVC 2019 Bazel 0.27.1-0.29.1
tensorflow-2.0.0 3.5-3.7 MSVC 2017 Bazel 0.26.1
tensorflow-1.15.0 3.5-3.7 MSVC 2017 Bazel 0.26.1
tensorflow-1.14.0 3.5-3.7 MSVC 2017 Bazel 0.24.1-0.25.2
tensorflow-1.13.0 3.5-3.7 MSVC 2015 update 3 Bazel 0.19.0-0.21.0
tensorflow-1.12.0 3.5-3.6 MSVC 2015 update 3 Bazel 0.15.0
tensorflow-1.11.0 3.5-3.6 MSVC 2015 update 3 Bazel 0.15.0
tensorflow-1.10.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.9.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.8.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.7.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.6.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.5.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.4.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.3.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.2.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.1.0 3.5 MSVC 2015 update 3 Cmake v3.6.3
tensorflow-1.0.0 3.5 MSVC 2015 update 3 Cmake v3.6.3
GPU
版本 Python 版本 编译器 构建工具 cuDNN CUDA
tensorflow_gpu-2.6.0 3.6-3.9 MSVC 2019 Bazel 3.7.2 8.1 11.2
tensorflow_gpu-2.5.0 3.6-3.9 MSVC 2019 Bazel 3.7.2 8.1 11.2
tensorflow_gpu-2.4.0 3.6-3.8 MSVC 2019 Bazel 3.1.0 8.0 11.0
tensorflow_gpu-2.3.0 3.5-3.8 MSVC 2019 Bazel 3.1.0 7.6 10.1
tensorflow_gpu-2.2.0 3.5-3.8 MSVC 2019 Bazel 2.0.0 7.6 10.1
tensorflow_gpu-2.1.0 3.5-3.7 MSVC 2019 Bazel 0.27.1-0.29.1 7.6 10.1
tensorflow_gpu-2.0.0 3.5-3.7 MSVC 2017 Bazel 0.26.1 7.4 10
tensorflow_gpu-1.15.0 3.5-3.7 MSVC 2017 Bazel 0.26.1 7.4 10
tensorflow_gpu-1.14.0 3.5-3.7 MSVC 2017 Bazel 0.24.1-0.25.2 7.4 10
tensorflow_gpu-1.13.0 3.5-3.7 MSVC 2015 update 3 Bazel 0.19.0-0.21.0 7.4 10
tensorflow_gpu-1.12.0 3.5-3.6 MSVC 2015 update 3 Bazel 0.15.0 7.2 9.0
tensorflow_gpu-1.11.0 3.5-3.6 MSVC 2015 update 3 Bazel 0.15.0 7 9
tensorflow_gpu-1.10.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 7 9
tensorflow_gpu-1.9.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 7 9
tensorflow_gpu-1.8.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 7 9
tensorflow_gpu-1.7.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 7 9
tensorflow_gpu-1.6.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 7 9
tensorflow_gpu-1.5.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 7 9
tensorflow_gpu-1.4.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 6 8
tensorflow_gpu-1.3.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 6 8
tensorflow_gpu-1.2.0 3.5-3.6 MSVC 2015 update 3 Cmake v3.6.3 5.1 8
tensorflow_gpu-1.1.0 3.5 MSVC 2015 update 3 Cmake v3.6.3 5.1 8
tensorflow_gpu-1.0.0 3.5 MSVC 2015 update 3 Cmake v3.6.3 5.1 8




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律