数据结构相关知识
一、什么是数据结构?
数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。
简单来说,数据结构就是设计数据以何种方式组织并存储在计算机中。
比如:列表、集合与字典等都是一种数据结构。
“程序=数据结构+算法”
二、数据结构的分类
数据结构按照其逻辑结构分为线性结构、数结构、图结构
- 线性结构:数据结构中的元素存在一对一的相互关系
- 树结构:数据结构中的元素窜在一对多的相互关系
- 图结构:数据结构中的元素存在多对多的相互关系
三、线性结构
1.栈
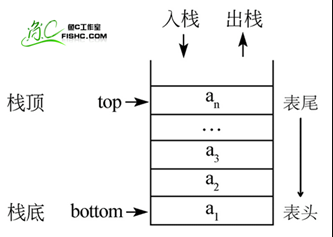
1、定义:栈是一个数据集合,可以理解为只能在一端进行插入或者删除操作的列表。
2、栈的特点:后进先出(last-in,first-out),简称LTFO表
3、栈的概念:
- 栈顶:允许插入和删除的这一端称之为栈顶
- 栈底:另一固定的一端称为栈底
- 空栈:不含任何元素的栈称为空栈
4、栈的基本操作:
- 进栈(压栈):push
- 出栈:pop
- 取栈顶:gettop
如图:

- 栈的python实现
不需要自己定义,使用列表结构即可
- Stack() 创建一个空的新栈。 它不需要参数,并返回一个空栈。
- push(item)将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。
- pop() 从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。
- peek() 从栈返回顶部项,但不会删除它。不需要参数。 不修改栈。
- isEmpty() 测试栈是否为空。不需要参数,并返回布尔值。
- size() 返回栈中的 item 数量。不需要参数,并返回一个整数。
class Stack():
#构造一个空战
def __init__(self):
self.items=[]
def push(self,item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return len(self.items)-1
def isEmpty(self):
return self.items ==[]
def size(self):
return len(self.items)
s = Stack()
print(s.isEmpty())
s.push(1)
s.push(2)
s.push(3)
print(s.pop())
print(s.pop())
print(s.pop())
# 输出结果:
True
3
2
1
2.队列
-
介绍
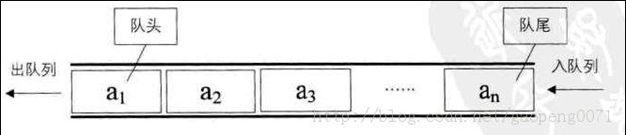
- 队列是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除,
- 进行插入的一端称为队尾(rear),插入动作称之为进队或入队
- 进行删除的一端称之为对头(front),删除动作称为出队
双向队列:对列的两端都允许进行进队和出队操作
-
队列的实现
队列能否简单用列表实现?为什么
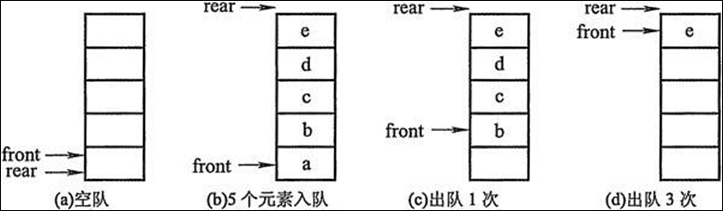
- 初步设想:列表+两个下标指针
- 创建一个列表和两个变量,front变量指向队首,rear变量指向队尾。初始时,front和rear都为0。
- 进队操作:元素写到li[rear]的位置,rear自增1。
- 出队操作:返回li[front]的元素,front自减1。
-
示例
- Queue() 创建一个空的新队列。 它不需要参数,并返回一个空队列。
- enqueue(item) 将新项添加到队尾。 它需要 item 作为参数,并不返回任何内容。
- dequeue() 从队首移除项。它不需要参数并返回 item。 队列被修改。
- isEmpty() 查看队列是否为空。它不需要参数,并返回布尔值。
- size() 返回队列中的项数。它不需要参数,并返回一个整数。
class Queue(): def __init__(self): self.items = [] def enqueue(self,item): self.items.insert(0,item) def dequeue(self): return self.items.pop() def isEmpty(self): return self.items == [] def size(self): return len(self.items) q = Queue() q.enqueue(1) q.enqueue(2) q.enqueue(3) print(q.dequeue()) print(q.dequeue()) print(q.dequeue()) # 结果为 123
-
案例:烫手的山芋
- 烫手山芋游戏介绍:6个孩子围城一个圈,排列顺序孩子们自己指定。第一个孩子手里有一个烫手的山芋,需要在计时器计时1秒后将山芋传递给下一个孩子,依次类推。规则是,在计时器每计时7秒时,手里有山芋的孩子退出游戏。该游戏直到剩下一个孩子时结束,最后剩下的孩子获胜。请使用队列实现该游戏策略,排在第几个位置最终会获胜。
- 提取有价值的信息:
- 计时1s的时候删除在第一个孩子手里面
- 山芋会被1s传递一次
- 7秒钟山芋被传递了6次
- 准则:保证第一个(队头)孩子手里面永远要有山芋
kids = ['A','B','C','D','E','F'] q = Queue() for kid in kids: q.enqueue(kid) while q.size() > 1:#当队列中孩子的个数大于1游戏继续否则游戏结束 for i in range(1,7):#山芋传递的次数 #对头元素出队列在入队列 kid = q.dequeue() q.enqueue(kid) q.dequeue()#一轮游戏结束后,将对头孩子淘汰(对头孩子手里永远有山芋)
3.双端队列 待完成
-
介绍
- 同同列相比,有两个头部和尾部。可以在双端进行数据的插入和删除,提供了单数据结构中栈和队列的特性
-
实例
- Deque() 创建一个空的新 deque。它不需要参数,并返回空的 deque。
- addFront(item) 将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
- addRear(item) 将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
- removeFront() 从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
- removeRear() 从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
- isEmpty() 测试 deque 是否为空。它不需要参数,并返回布尔值。
- size() 返回 deque 中的项数。它不需要参数,并返回一个整数。
双端队列应用案例:回文检查 待补充
- 回文是一个字符串,读取首尾相同的字符,例如,radar toot madam。
class Queue(): def __init__(self): self.items = [] def addFront(self,item): self.items.insert(0,item) def addRear(self): self.items.append(self) def removeFront(self): self.items.pop(0) def size(self): return len(self.items)
4. 顺序表
-
概念
- 集合中存储的元素是有顺序的,顺序表的结构可以分为两种形式:单数据类型和多数据类型。
- python中的列表和元组就属于多数据类型的顺序表
- 列表,元组,字典等属于python中的高级数据结构,现在我们研究的是存储的本质,所以不用这些高级结构;
这里我们要使用的是内存存储,计算机中的内存时用来存储数据以及和cpu打交道的;
-
位,比特bit,字节Byte,字之间的关系
1位=1bit比特; 1Byte字节=8位; 1字=2Byte字节; 1字=16位。 1 bit = 1 二进制数据 1 byte = 8 bit 1 字母 = 1 byte = 8 bit 1 汉字 = 2 byte = 16 bit 一个二进制数据0或1,是1bit; 存储空间的基本计量单位,如:MySQL中定义 VARCHAR(45) 即是指 45个字节; 1 byte = 8 bit 字母 = 1 byte = 8 bit -
顺序表单数据类型的基本格式
内存的基本单位是1Byte;
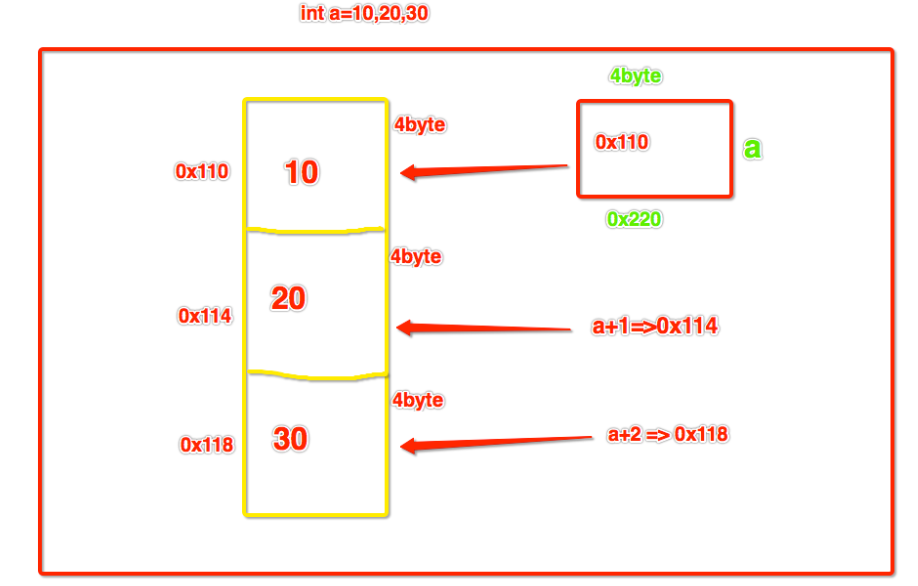
内存是一个连续的存储空间;int a = 1在内存中存储时,占了四个存储单元,即占了4*8bit;
一个字符即一个char占一个字节存储单元;
基础数据类型不同,所占用的存储单元也不同;
在存储的时候,如果存储的是数字,那么在取连续的四个存储单元是会当做一个整体取出然后转换为一个数字;如果存储的是一个字符,那么取的时候会当做四个字符取出;
存储数字1的时候,会在内存中存储 00000000 00000000 00000000 00000001;0x01 00000000 0x02 00000000 0x03 00000000 0x04 00000001在存储一组数据 1,2,3 时,我们要将这三个数字在内存中连续的存储,以方便取出;
那么就是0x01 1 0x05 2 0x09 3这样存储的;
我们可以这样理解,当我们存储一个纯数字列表的时候,存储了列表第一个元素在内存中的初始位置,当我们要按照下标去取数据的时候,因为数据在内存中是连续存储的,假设存储的第一个数据是0x01,那么第二个数据就是 0x0(1+4),第三个数据是 0x0(1+4*2),即按照数据的下标进行数据偏移即可;
所以当一组数据全部是相同数据类型时,我们按照一组数据在内存中紧靠在一起存放,那么这种数据存储形式就叫做顺序表;编程语言中的索引从0开始的原因是存储数据时,变量指向的是第一个元素的内存位置,它的偏移量为0,即索引的0代表的就是偏移量为0;
-
顺序表多数据类型
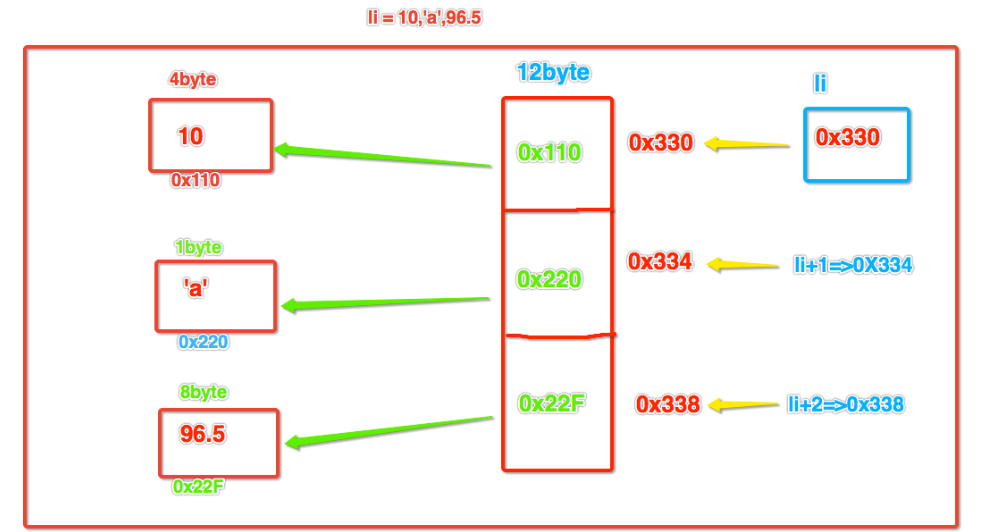
-
总结
- 单数据类型顺序表的内存图(内存连续开启)
- 多数据类型顺序表的内存图(内存非连续开辟)
- 顺序表的弊端:顺序表的结构需要预先知道数据大小来申请连续的存储空间,而在进行扩充时又需要进行数据的搬迁
5.链表 待完成
链表中每一个元素都是一个对象,每一个对象都是一个节点,包含有数据域key和指向下一个节点的指针next。通过各个节点之间的互相连接,最终串联成一个列表

is_empty():链表是否为空
. length():链表长度
. travel():遍历整个链表
. add(item):链表头部添加元素
. append(item):链表尾部添加元素
. insert(pos, item):指定位置添加元素
. remove(item):删除节点
. search(item):查找节点是否存在
-
节点定义:
class Node(): def __init__(self,item) self.item = item # 为了存储数值数据 self.next = None # 为了存储下一个节点的地址 -
建立链表
class Link(): #构建一个空链表 def __init__(self): #_head要指向第一个节点,,如果没有节点则指向None self._head = None def add(self,item): #1.创建一个新节点 node = Node(item) node.next = self._head self._head = node def is_empty(self): return self._head == None def length(self): cur = self._head count = 0#记录节点的个数 while cur: count += 1 cur = cur.next return count -
链表的遍历
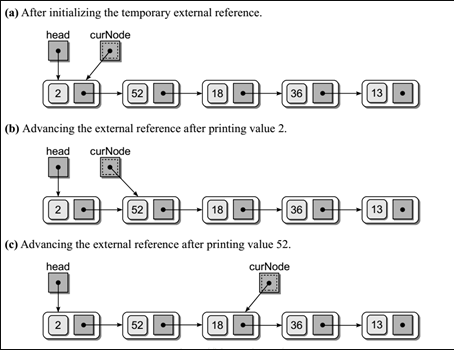
# 继创建链表类中继续写方法 def travel(self): #在非空的链表中head永远要指向第一个节点的地址 ,永远不要修改它的指向,否则会造成数据的丢失 cur = self._head while cur: print(cur.item) cur = cur.next -
链表的添加
# 继创建链表类中继续写方法 def append(self,item): node = Node(item) cur = self._head #当前节点 pre = None #指向cur的前一个节点 if self._head == None:#如果链表为空则需要单独处理 self._head = node return while cur: pre = cur cur = cur.next#循环结束之后cur指向了None,pre指向了最后一个节点 pre.next = node -
链表的插入和删除
-
插入
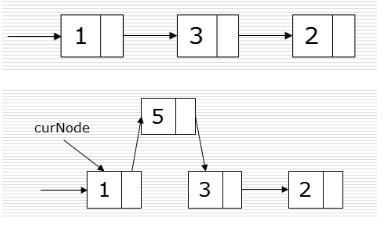
# 继创建链表类中继续写方法 def insert(self,pos,item) node = Node(item) cur = self._head#当前节点 pre = None #如果插入的位置大于了链表的长度,则默认插入到尾部 if post > self.length()-1: self.append(item) return #否则 查找要插入的节点 for i in range(pos): pre = cur# 指向cur的前一个节点 cur = cur.next# pre.next = node node.next = cur -
删除
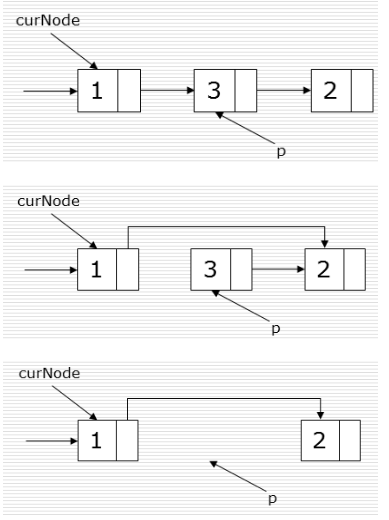
# 继创建链表类中继续写方法 def remove(self,item): cur = self._head#当前节点 pre = None# cur的前一个节点 if item == cur.item:# 如果删除的元素和第一个节点相同 self._head = cur.next# 则head指向下一个节点 return while cur: if cur.item != item:# 如果当前节点 不等于要删除的节点 pre = cur# cur的前一个节点 cur = cur.next# 下一个节点 else: break # cur前一个节点next 值为 cur下一个节点 pre.next = cur.next
-
-
完整版
class Node(): def __init__(self,item): self.item = item #为了存储数值数据 self.next = None #为存储下一个节点的地址 class Link(): #构建一个空链表 def __init__(self): #_head要指向第一个节点,如果没有节点则指向None self._head = None def add(self,item): #1.创建一个新节点 node = Node(item) node.next = self._head self._head = node def travel(self): # print(self._head.item) # print(self._head.next.item) # print(self._head.next.next.item) #在非空的链表中head永远要指向第一个节点的地址,永远不要修改它的指向,否则会造成数据的丢失 cur = self._head while cur: print(cur.item) cur = cur.next def is_empty(self): return self._head == None def length(self): cur = self._head count = 0#记录节点的个数 while cur: count += 1 cur = cur.next return count def append(self,item): node = Node(item) cur = self._head #当前节点 pre = None #指向cur的前一个节点 if self._head == None:#如果链表为空则需要单独处理 self._head = node return while cur: pre = cur cur = cur.next#循环结束之后cur指向了None,pre指向了最后一个节点 pre.next = node # 要查找的item def search(self,item): cur = self._head# cur为开始节点 find = False# 查找状态 while cur: if cur.item == item:# 如果cur的值为查找的item值 find = True break#退出循环 else: cur = cur.next# cur为下一个节点的值 return find def insert(self,pos,item): node = Node(item) cur = self._head pre = None #如果插入的位置大于了链表的长度,则默认插入到尾部 if pos > self.length()-1: self.append(item) return for i in range(pos): pre = cur cur = cur.next pre.next = node node.next = cur def remove(self,item): cur = self._head pre = None if item == cur.item: self._head = cur.next return while cur: if cur.item != item: pre = cur cur = cur.next else: break pre.next = cur.next
6.双向链表
双向链表:一种更复杂的链表是 "双向链表" 或 "双面链表"。每个节点有两个链接:一个指向前一个节点,当次节点为第一个节点时,指向空值;而另一个指向下一个节点,当此节点为最后一个节点时,指向空值。
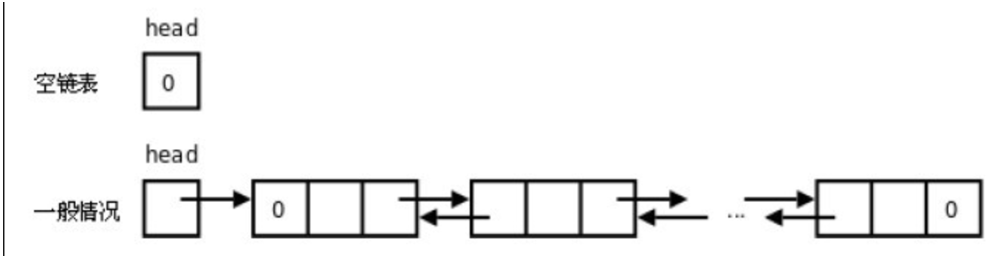
代码实现
# coding=utf-8
# 双向链表
class Node:
"""节点"""
def __init__(self, item):
self.item = item
self.prev = None
self.next = None
class DLinkList:
"""双向链表"""
def __init__(self):
self._head = None
def is_empty(self):
"""判断链表是否为空"""
return self._head is None
def length(self):
"""获取链表长度"""
if self.is_empty():
return 0
else:
cur = self._head
count = 1
while cur.next is not None:
count += 1
cur = cur.next
return count
def travel(self):
"""遍历链表"""
print("↓↓" * 10)
if self.is_empty():
print("")
else:
cur = self._head
print(cur.item)
while cur.next is not None:
cur = cur.next
print(cur.item)
print("↑↑" * 10)
def add(self, item):
"""链表头部添加节点"""
node = Node(item)
if self.is_empty():
self._head = node
else:
cur = self._head
node.next = cur
cur.prev = node
self._head = node
def append(self, item):
"""链表尾部添加节点"""
node = Node(item)
if self.is_empty():
self._head = node
else:
cur = self._head
# 遍历找到最后一个节点
while cur.next is not None:
cur = cur.next
# 在尾节点添加新的节点
cur.next = node
node.prev = cur
def insert(self, pos, item):
"""指定位置添加"""
# 头部添加
if pos <= 0:
self.add(item)
# 尾部添加
elif pos > (self.length() - 1):
self.append(item)
# 其他位置添加
else:
node = Node(item)
cur = self._head
cur_pos = 0
while cur.next is not None:
if cur_pos == (pos - 1):
# 与下一个节点互相指向
node.next = cur.next
cur.next.prev = node
# 与上一个节点互相指向
cur.next = node
node.prev = cur
cur_pos += 1
cur = cur.next
def remove(self, item):
"""删除节点"""
if self.is_empty():
return
else:
cur = self._head
# 删除首节点
if cur.item == item:
self._head = cur.next
cur.next.prev = None
# 删除其他节点
else:
while cur.next is not None:
if cur.item == item:
# 删除之前:1 ←→ [2] ←→ 3
# 删除之后:1 ←→ 3
cur.prev.next = cur.next
cur.next.prev = cur.prev
cur = cur.next
# 删除尾节点
if cur.item == item:
cur.prev.next = None
def search(self, item):
"""查找节点是否存在"""
if self.is_empty():
return -1
else:
cur = self._head
cur_pos = 0
while cur.next is not None:
if cur.item == item:
return cur_pos
cur_pos += 1
cur = cur.next
if cur_pos == (self.length() - 1):
return -1
if __name__ == "__main__":
ll = DLinkList()
ll.add(1) # 1
ll.add(2) # 2 1
ll.append(3) # 2 1 3
ll.insert(2, 4) # 2 1 4 3
ll.insert(4, 5) # 2 1 4 3 5
ll.insert(0, 6) # 6 2 1 4 3 5
print("length:", ll.length()) # 6
ll.travel() # 6 2 1 4 3 5
print("search(3)", ll.search(3))
print("search(4)", ll.search(4))
print("search(10)", ll.search(10))
ll.remove(1)
print("length:", ll.length())
ll.travel()
print("删除首节点 remove(6):")
ll.remove(6)
ll.travel()
print("删除尾节点 remove(5):")
ll.remove(5)
ll.travel()
7.面试题:如何将单链表倒序?
def reverse(self):
if self._head:
cur = self._head
pre = None
cur_next = cur.next
if cur.next is None:
return
while True:
cur.next = pre
pre = cur
cur = cur_next
if cur == None:
self._head = cur
break
cur_next = cur_next.next
self._head = pre



