领域自适应(Domain Adaptation)之领域不变特征适配(二)
在前面一节领域自适应(Domain Adaptation)之领域不变特征适配(一)中,我们利用MMD公式来对齐两个边缘分布\(P(Z)\)和\(Q(Z)\),学习领域不变特征。本章节通过另一种方法来学习领域不变特征————对抗训练。
一个例子
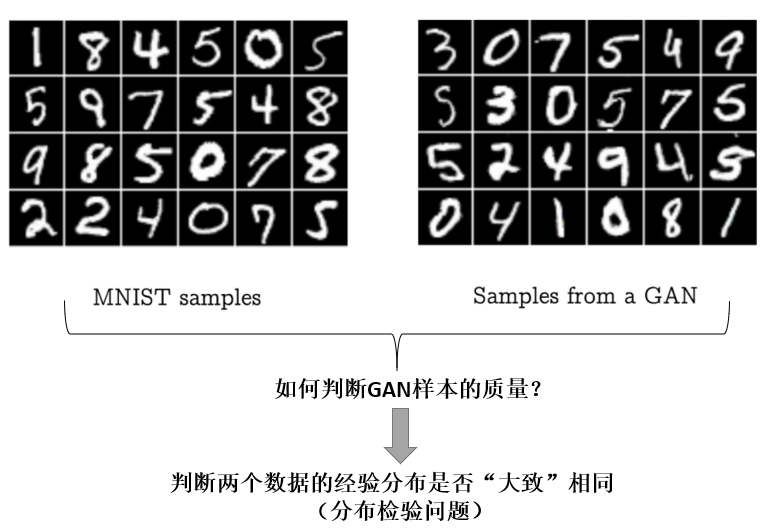
假设现在有两堆数据,一堆是真实的样本来自MINST数据集,一堆是通过GAN生成的样本。如何判断GAN生成样本的质量呢?
可以使用直接使用MMD来做测试!
也可以使用基于参数估计的方法:
假设MINST数据集\(D_s=\{x_i^s\}\),GAN生成样本数据集\(D_t=\{x_j^t\}\),现在给这些数据打上标签,如果\(x\)来自MINST,则打上标签1,若来自GAN,则打上标签0,即
- 基于所有的数据\(\{D_S,D_t\}\),训练一个binary分类器\(h:\mathcal{X}\mapsto [0,1]\),
- 给定一个由GAN生成的测试样本\(y\),若\(h(y)\)的得分越接近0.5,则说明GAN样本的质量越好,分类器很难将GAN生成的样本与真实的MINST数据集作出区分;如果越接近0,则说明生成的质量越差。
- 由此,可以定义一个泛化误差,
err越大,说明越难以区分,GAN质量越高;相反,则越容易区分,GAN生成的样本与MINST有明显差别,生成的质量越差。
4. 由此,我们得到了一个常用的测量工作\(\mathcal{A}\)-distance,
思想:与基于MMD的方法不同,基于对抗训练的UDA方法就是构建一个额外的判别器\(h\)用于判断样本的特征来自哪个域,然后训练一个统一的特征抽取器去“糊弄”\(h\),让其\(\mathcal{A}\)-distance尽可能的小,无法分辨出特征来自哪个域,以获取域间的“共享特征”。
最大均值差异MMD与GAN
在原始的GAN中,其损失函数是
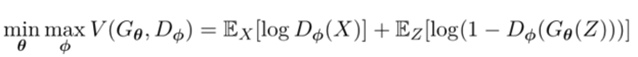
其中判别器\(D\)的作用是判别样本\(x\)是真实的样本还是\(G\)生成的样本,然后促使\(G\)生成更逼真的样本来糊弄\(D\)。
GAN的真实目的是让生成样本分布与真实样本分布达到一致。这与MMD的作用是一样的,所以传统的GAN方法其实是可以用MMD来实现的,以实现两个分布间的对齐(一致)。
我们利用MMD得到一个新的损失函数(参考工作 Y. Li et al. Generative moment matching networks. ICML2015),
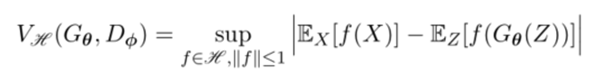
其原理图是
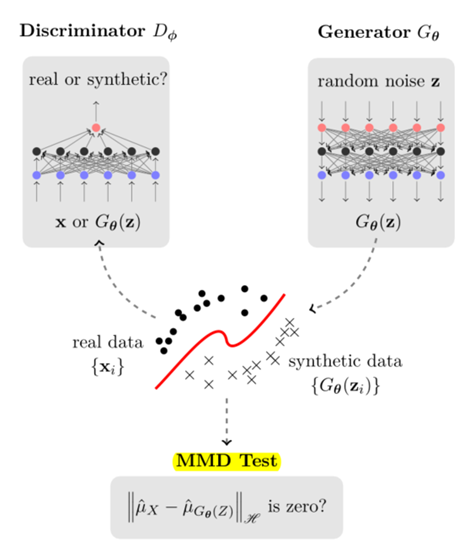
这样做的优点是MMD提供了一个closed-form的解,而且理论上与GAN是近似的;避免了对抗训练带来的不稳定性。
基于对抗训练的UDA
(工作来源:Ganin et al. Unsupervised Domain Adaptation by Backpropagation. ICML 2015.)
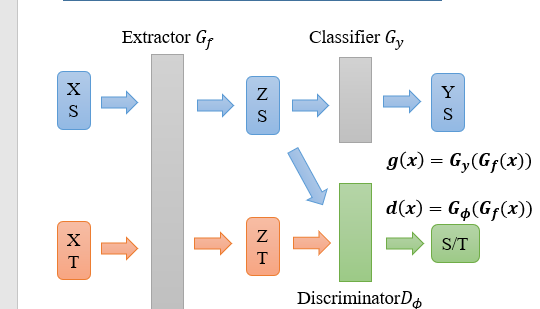
我们已经介绍了基于MMD的UDA方法,其实可以将MMD换成一个判别器来抽取领域不变的特征。
模型的基本结构
我们构造两个损失函数,一个是源域的交叉熵,一个是判别器区分特征来自哪个域的binary损失。
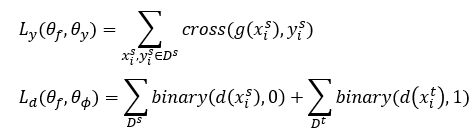
训练的规则如下,

反转梯度层 Gradient Reversal Layers (GRL)

特征抽取器\(G_f\)即有正向的梯度,又有反向的梯度,这是很难用现有的SGD来解决的。
我们可以定义一种伪函数,其正向传播是保持不变的,其反向传播是会变成负向的梯度

基于这样的设计,
我们把\(L_d\)中的\(d(x)\)作下转化,得到新的损失函数\(L_{nd}\),

这时的新训练目标转换为,

我们通过引入伪函数把一个最大最小问题转化为一个最小问题
解释:

反向传播的时候自然会把负号引入进来。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号