领域自适应（Domain Adaptation）之领域不变特征适配（一）

无监督领域自适应（Unsupervised domain adaptation, UDA）

任务描述

现有两个数据集，

\[\mathcal{D}_s=\{(x^s_i,y^s_i)\}_{i=1}^{m} \]

\[\mathcal{D}_t=\{x^t_j\}_{j=1}^{n} \]

源域（Source Domain）\(\mathcal{D}_s\)和目标域（Target Domain）\(\mathcal{D}_t\)的数据经验分布不一样，但是任务是相同的。
任务是利用源域中已有的知识（标签信息）去学习目标域的样本的类别。

直观感受

如现在有两堆数据，一堆是真实的动物照片，一堆是手绘动物的照片。两个数据集的风格是明显不一样的，它们的分布也是明显存在偏差的。如果我们直接在真实的动物照片上训练一个分类器，然后直接用在手绘动物的照片的分类上，性能必然是比较差的。
每个领域都有自己特有的知识，而这些特有的知识对其它领域反而是一种干扰

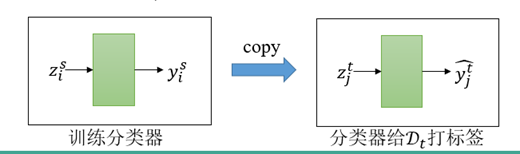
在UDA任务中，我们需要寻找一种“共有特征”。如在上面的照片中，对于真实的猴子和手绘的猴子，我们需要提炼出猴子的共有特征，如脸庞的形状，毛发的颜色等，摒弃一些领域自己特有的特征，如图片的背景，构图差异等。
假设我们现在有一个特征抽取器\(f:\mathcal{X}\mapsto \mathcal{Z}\)，可以抽取出“共有特征”，则根据这个\(f\)，我们可以构建出两个新的数据集，

\[\mathcal{D}_s=\{(z^s_i=f(x^s_i),y^s_i)\}_{i=1}^{m} \]

\[\mathcal{D}_t=\{z^t_j=(x^t_j)\}_{j=1}^{n} \]

\(\mathcal{D}_s\)相当于我们的训练集，而\(\mathcal{D}_t\)就是我们的测试集。我们在训练集\(\mathcal{D}_s\)上直接训练一个分类器，然后用分类器对\(\mathcal{D}_t\)进行分类任务，即可完成UDA任务。

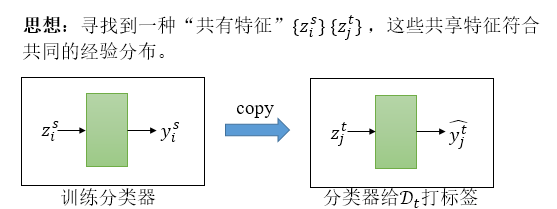
我们把“共有特征”称作“领域不变特征”。

下面我们回顾一下一个重要的工具叫做最大均值差异，利用它就可以抽取领域不变特征。

最大均值差异（Maximum Mean Discrepancy, MMD）

细节请参考我以前的帖子

1. 浅谈Maximum Mean Discrepancy (MMD)
2. 核均值嵌入（KME， kernel mean embeddings）
3. 再生核Hilbert空间（RKHS）

核心思想

MMD用于检验两堆数据是否来源于同一个分布，

\[\mathcal{D}_s=\{x_i\}_{i=1}^{m}\sim P \]

\[\mathcal{D}_t=\{y_j\}_{j=1}^{n} \sim Q \]

MMD用于检验\(P=Q\)。

MMD的经验公式为，

\[\widehat{\text{MMD}}(P,Q)^2=\frac{1}{m^2}\sum_{i,j} k(x_i,x_j)+\frac{1}{n^2}\sum_{i,j} k(y_i,y_j)-\frac{2}{mn}\sum_{i,j}k(x_i,y_j) \]

用这个公式可以衡量两个分布之间的“距离”，如果MMD=0，则两个分布是一样的，如果MMD很大，说明两个分布明显是不一致的。
\(k(x,y)\)是核函数，常见的核包括
高斯核：

\[k(x,y)=\exp \left(-\frac{\|x-y\|^2}{\delta} \right) \]

拉普拉斯核：

\[k(x,y)=\exp \left(-\frac{\|x-y\|}{\delta} \right) \]

基于MMD的领域自适应方法

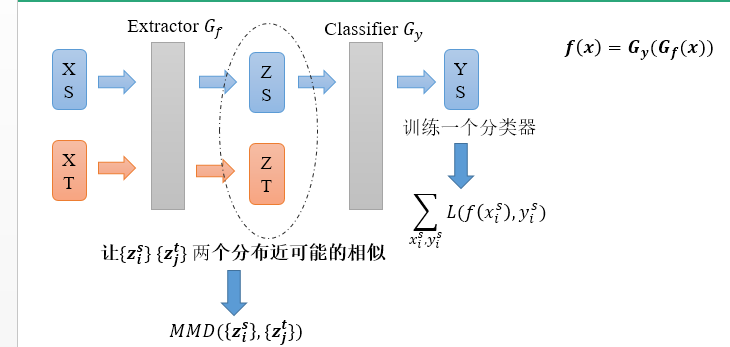
模型的基本结构很简单，包括一个特征抽取器\(G_f:\mathcal{X}\mapsto \mathcal{Z}\)和一个特征分类器\(G_y:\mathcal{Z}\mapsto\mathcal{Y}\)。该模型与传统的分类模型是一致的，\(f(x)=G_y(G_f(x))\)。
现在我们有两个数据流，一个是输入源域数据\(x^s\)，经过\(G_f\)变成特征\(z^s\)，然后经过\(G_y\)变成类概率\(\hat y^s\)。我们源域有真实的标签\(y^s\)，所有我们可以构建一个分类loss函数,

\[L_y=\frac{1}{m}\sum_{i=1}^{m}L(f(x_i^s),y_i^s) \]

其中\(L\)是交叉熵损失。这个与传统的分类任务没有任何区别。

下面，还有一个更重要的任务，就是寻找“领域不变”的特征。
经过特征抽取器\(G_f\)，我们把所有的源域样本和目标域样本映射到特征空间，

\[Z^s=\{z^s_1,z^s_2,\cdots,z^s_m\}\sim P \]

\[Z^t=\{z^t_1,z^t_2,\cdots,z^t_n\}\sim Q \]

我们的目标是寻找一种领域不变特征，即让分布\(P\)和\(Q\)之间的“距离”越来越少，让两个分布一样，即可说明我们找到了源域和目标域一个共同的表示空间。

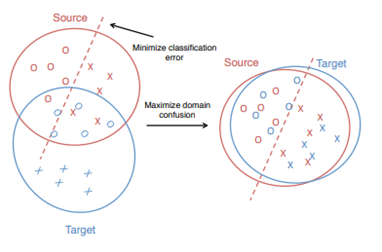
我们可以用MMD来衡量P和Q之间的距离，并希望在训练过程中，\(G_f\)能学习这样一组特征，使得MMD越来越小.
所以我们可以构造这样一个loss函数,

\[L_A = MMD(Z^s,Z^t) \]

联合以上两个loss，我们可以联合训练一个简单的领域自适应模型，

\[L=\frac{1}{m}\sum_{i=1}^{m}L(f(x_i^s),y_i^s) + \lambda MMD(Z^s,Z^t) \]

所存在的问题

这类方法存在一个非常明显的问题，就是 你很难保证你抽取出来的领域不变特征能够包含类别信息。如在上面猴子的例子中，抽取出来的领域不变特征可能并不包含猴子的关键特征，不能通过这些特征辨别出它是一只猴子还是一只猩猩。这一类能够“辨识”类别的特征有一个专用的名字叫做 判别特征。

这些领域不变的方法有一个假设前提：
假设\(P(Z)\)和\(Q(Z)\)是相似的，则有\(P(Y|Z)\)和\(Q(Y|Z)\)也是相似的。
实际上，很多时候这个假设前提并不能够被保证。

因此现在很多UDA方法开始探索对齐条件分布\(P(Y|Z)\)和\(Q(Y|Z)\)来寻找判别特征。我们下面将会详细的介绍几种典型的方法。