剑指offer-面试题41：数据流中的中位数

题目描述：如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

题目分析：首先题目要求是从数据流中读取一个数据，这也就意味着，数据容器中的数据是在不断变化的，因此这里首先要考虑的一个问题就是：在将新读取到的数据插入到数据容器中时，要保证其时间效率下表是不同的数据结构下，所需要的时间复杂度

数据结构	插入的时间复杂度	得到中位数的时间复杂度
没有排序的数组	O(1)	O(n)
排序的数组	O(n)	O(1)
排序的链表	O(n)	O(1)
二叉搜索树	平均O(logn),最差O(n)	平均O(logn),最差O(n)
AVL(平衡的二叉搜索树)	平均O(logn)	平均O(1)
最大堆和最小堆	平均O(logn)	平均O(1)

在这里不使用AVL树，而使用最大堆和最小堆的原因在于，在面试时短时间内，不太可能构造出一颗适合本例题的AVL树，因此此处使用最大、最小堆。

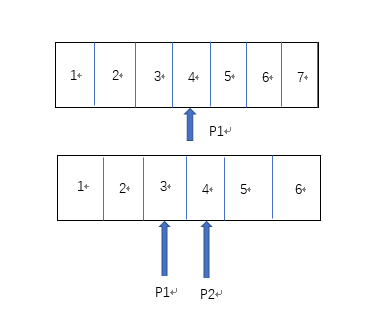
如上图所示，如果数据已经在容器中有序，并且如果容器中数据的个数为偶数，那么中位数可以由P1和P2指向的数求平均得到，如果为奇数，则中位数为P1指向的数。

我们可以发先容器被封分割成了两个部分。位于容器左边的数据比右边的数据小。P1指向的是左边的最大数，P2指向的是右边的最小数。基于以上思路：用一个最大堆实现左边的数据容器，用一个最小堆实现右边的数据容器。

具体代码如下：
import java.util.PriorityQueue;
import java.util.Comparator;
public class Solution {
   PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();//优先队列默认为小顶堆
   //通过比较器，实现大顶堆
   PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(11,new Comparator<Integer>(){
   public int compare(Integer i, Integer j)
   {
       return j-i;
   }
   });
    public void Insert(Integer num) {
        //如果已经读取到的数为偶数个，则下一个读取到的数将放入小顶堆中
        if(((minHeap.size()+ maxHeap.size())&1)==0)//已经读取到的数为偶数个，下一个读进来变为奇数个
        {
        //判断如果大顶堆不为空，并且插入的数字比大顶堆最大的数字小
             if(!maxHeap.isEmpty() && maxHeap.peek() > num)
             {
                  //首先将数据插入到大顶堆中
                  maxHeap.offer(num);
                  num = maxHeap.poll();
             }
                   //如果maxHeap.peek()<num,将新读取到的数字插入小顶堆中
                  minHeap.offer(num);
        }
        else
        {
        //如果已经读取到的数为奇数个，即小顶堆数量比大顶堆多一，将新读取到的数插入到大顶堆中
            if(!minHeap.isEmpty()&& minHeap.peek()<num)
            {
                minHeap.offer(num);
                num = minHeap.poll();
            }
            //如果MinHeap.peek() > num,则直接插入大顶堆中
            maxHeap.offer(num);
        }
    }

    public Double GetMedian() {
        if((minHeap.size()+maxHeap.size()) == 0)
        {
            throw new RuntimeException();
        }
        double median;
        if(((minHeap.size() + maxHeap.size()) & 1 )== 0 )
        {
            median = (minHeap.peek() + maxHeap.peek()) / 2.0;
        }
        else
        {
           median = minHeap.peek();
        }
        return median;
    }
}

PriorityQueue是基于堆实现的数据结构，其逻辑结构是一颗完全二叉树，存储结构其实是一个数组。PriorityQueue，也叫优先级队列，它是不同于先进先出队列的另一种队列。每次从队列中取出的是具有最高优先权的元素。
如果不提供Comparator的话，优先队列中元素默认按自然顺序排列，也就是数字默认是小的在队列头，字符串则按字典序排列。也就是说我们通过设置comparator比较器来定义优先级别。

有以下代码：

//小顶堆

public static void MinPriorityQueue()
{
    PriorityQueue<Integer> queue = new PriorityQueue<Integer>(10);
    //入队
    for(int i = 10; i >=5;i--)
    {
        queue.offer(i);

    }
    //遍历元素
    for(Integer i : queue)
    {
        System.out.print(i+" ");
    }
    System.out.println();
}

这段代码的打印结果为：打印小顶堆中的元素：5 7 6 10 8 9 ，并不是有序的，不是按照5，6，7，8，9，10输出，原因在于：小顶堆只是保证了根节点不大于左右两个节点，但是左右两个节点谁比谁大并不能保证，也就是说队列的元素，在物理结构上是数组，是无序的。

//大顶堆

public static void MaxPriorityQueue()
{
    //通过比较器实现大顶堆
    PriorityQueue<Integer> queue = new PriorityQueue<Integer>(10,new Comparator<Integer>() {
        public int compare(Integer o1, Integer o2) {
            return o2.compareTo(o1);
        }
    });
    for(int i = 10; i >=5;i--)
    {
        queue.offer(i);
    }
    //打印
    for(Integer i : queue)
    {
        System.out.print(i);
    }
}

输出结果：10，9，8，7，6，5
队列在物理上是数组，是无序的，但是其逻辑结构是小顶堆，是有序的。那么如何让小顶堆也按照5，6，7，8，9，10输出呢？可以通过以下代码：

public static void minPriorityQueueOrder()
{
    PriorityQueue<Integer> queue = new PriorityQueue<Integer>(10);
    //入队
    for(int i = 10; i >=5;i--)
    {
        queue.offer(i);
    }
    //出队，采用priorityQueue中的内置方法，先使用peek()方法判断堆顶元素是否存在
    //然后使用poll()方法取出堆顶元素，并将其删除
    while(queue.peek() != null)
    {
        System.out.print(queue.poll()+ " ");
    }
}

总结：这里面用到了优先队列，首先优先队列本身就是一个小顶堆，可以通过比较器的方式实现大顶堆，另外还用到了priorityQueue中的一些方法：peek()、poll()、offer()；小顶堆只是保证了根节点不大于左右两个节点，但是左右两个节点谁比谁大并不能保证，也就是说队列的元素，在物理结构上是数组，是无序的；而大顶堆可以通过比较器的方式实现，并且遍历出来的顺序也同样有序。

附上完整的测试代码：

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Scanner;

public class MiddleNumber {
    //定义小顶堆
     PriorityQueue<Integer> minQueue = new PriorityQueue<Integer>();
     //通过比较器创建大顶堆
    PriorityQueue<Integer>  maxQueue = new PriorityQueue<Integer>(new Comparator<Integer>() {
         @Override
         public int compare(Integer o1, Integer o2) {
             return o2.compareTo(o1);
         }
     });
    //将数据流中获取到的数字放入堆中
    public void Insert(Integer num)
    {
        //如果当前读取到的数字为偶数个，则将当前数字放入小顶堆中
        if(((minQueue.size() + maxQueue.size()) & 1) == 0)
        {
            if(!maxQueue.isEmpty() && maxQueue.peek() > num)
            {
                maxQueue.offer(num);
                num = maxQueue.poll();
            }
            minQueue.offer(num);
        }
        //如果已经读取到的个数为奇数个，则将当前读取到的数字放入大顶堆中
        else
        {
            if(!minQueue.isEmpty() && minQueue.peek() < num)
            {
                minQueue.offer(num);
                num = minQueue.poll();
        }
            maxQueue.offer(num);
        }
    }
    //获取中位数
    public double getMediam()
    {
        if(minQueue.size() + maxQueue.size() == 0)
        {
            throw new RuntimeException();
        }
        if(((maxQueue.size()+minQueue.size())& 1) == 0)
        {
            return (minQueue.peek()+maxQueue.peek())/2.0;
        }
        else
        {
            return minQueue.peek();
        }
    }
    public static void main(String[] args)
    {
        MiddleNumber middleNumber = new MiddleNumber();
        Scanner sc = new Scanner(System.in);
        int c = 0;
        while(true)
        {
            System.out.println("请输入一个数字");
            c = sc.nextInt();
            middleNumber.Insert(c);
            System.out.println("当前的中位数为：" +   middleNumber.getMediam());
        }
    }
}