codeforces 689D D. Friends and Subsequences(RMQ+二分)
题目链接：
Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?
Every one of them has an integer sequences a and b of length n. Being given a query of the form of pair of integers (l, r), Mike can instantly tell the value of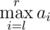 
while !Mike can instantly tell the value of 
.
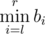Now suppose a robot (you!) asks them all possible different queries of pairs of integers (l, r) (1 ≤ l ≤ r ≤ n) (so he will make exactlyn(n + 1) / 2 queries) and counts how many times their answers coincide, thus for how many pairs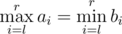 
is satisfied.
How many occasions will the robot count?
The first line contains only integer n (1 ≤ n ≤ 200 000).
The second line contains n integer numbers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the sequence a.
The third line contains n integer numbers b1, b2, ..., bn ( - 109 ≤ bi ≤ 109) — the sequence b.
Print the only integer number — the number of occasions the robot will count, thus for how many pairs 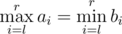is satisfied.
6
1 2 3 2 1 4
6 7 1 2 3 2
2
3
3 3 3
1 1 1
0
题意：
在一个区间[l,r]中a的最大值等于b的最小值,问这样的区间有多少个;
思路：
枚举左端点,二分找到右端点可行区间的左右边界;
在确定右段点的左右边界时,要用RMQ,
左边界:要是amax>=bmin,左移;否则右移,找到第一个amax=bmin的点;
右边界：要是amax>bmin,左移,否则右移,找到最后一个amax=bmin的点;
累加右端点可行区间长度即可;
AC代码：
//#include <bits/stdc++.h> #include <vector> #include <iostream> #include <queue> #include <cmath> #include <map> #include <cstring> #include <algorithm> #include <cstdio> using namespace std; #define For(i,j,n) for(int i=j;i<=n;i++) #define Riep(n) for(int i=1;i<=n;i++) #define Riop(n) for(int i=0;i<n;i++) #define Rjep(n) for(int j=1;j<=n;j++) #define Rjop(n) for(int j=0;j<n;j++) #define mst(ss,b) memset(ss,b,sizeof(ss)); typedef long long LL; template<class T> void read(T&num) { char CH; bool F=false; for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar()); for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar()); F && (num=-num); } int stk[70], tp; template<class T> inline void print(T p) { if(!p) { puts("0"); return; } while(p) stk[++ tp] = p%10, p/=10; while(tp) putchar(stk[tp--] + '0'); putchar('\n'); } const LL mod=1e9+7; const double PI=acos(-1.0); const LL inf=1e18; const int N=2e5+10; const int maxn=1005; const double eps=1e-10; int a[N],b[N],MX[N][21],MN[N][21],n; struct Tree { int l,r; int mmax,mmin; }tr[4*N]; void build(int o,int L,int R) { for(int i=1;i<=n;i++) MX[i][0]=a[i],MN[i][0]=b[i]; for(int j=1;(1<<j)<=n;j++) { for(int i=1;i+(1<<j)-1<=n;i++) { MX[i][j]=max(MX[i][j-1],MX[i+(1<<(j-1))][j-1]); MN[i][j]=min(MN[i][j-1],MN[i+(1<<(j-1))][j-1]); } } } int query(int o,int L,int R,int flag) { if(flag) { int k = 0; while( (1<<(k+1)) <= R-L+1) k ++ ; return max(MX[L][k],MX[R-(1<<k)+1][k]); } else { int k = 0; while( (1<<(k+1)) <= R-L+1) k ++ ; return min(MN[L][k],MN[R-(1<<k)+1][k]); } } int check(int x,int y,int flag) { int mx=query(1,x,y,1),mn=query(1,x,y,0); if(flag){ if(mx==mn)return 1; else if(mx>mn)return 2; return 0;} else { if(mx==mn)return 1; return 0; } } int main() { read(n); For(i,1,n)read(a[i]); For(i,1,n)read(b[i]); build(1,1,n); LL ans=0; int L,R; For(i,1,n) { int l=i,r=n; while(l<=r) { int mid=(l+r)>>1; if(!check(i,mid,1))l=mid+1; else r=mid-1; } L=l; if(check(i,L,1)==2)continue; l=L,r=n; while(l<=r) { int mid=(l+r)>>1; if(check(i,mid,0))l=mid+1; else r=mid-1; } R=l-1; if(R>=L)ans=ans+(R-L+1); } cout<<ans<<"\n"; return 0; }
