codeforces 688D D. Remainders Game(中国剩余定理)

题目链接：

D. Remainders Game

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Today Pari and Arya are playing a game called Remainders.

Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 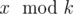. There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya  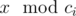if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value  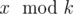for any positive integer x?

Note, that 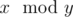 means the remainder of x after dividing it by y.

Input

The first line of the input contains two integers n and k (1 ≤ n,  k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 1 000 000).

Output

Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise.

Examples

input

4 5
2 3 5 12

output

Yes

input

2 7
2 3

output

No

题意：

给出c1,c2,...cn,问对于任何一个正整数x,给出x%c1,x%c2,...的值x%k的值是否确定;

思路：

中国剩余定理,给个链接：传送门


AC代码：

//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef  long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('\n');
}

const LL mod=1e9+7;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=1e6+20;
const int maxn=1005;
const double eps=1e-10;

int n,k;
LL c[N];
LL gcd(LL a,LL b)
{
    if(b==0)return a;
    return gcd(b,a%b);
}
int main()
{
        read(n);read(k);
        LL lcm=1;
        for(int i=1;i<=n;i++)
        {
            read(c[i]);
            lcm=c[i]/gcd(lcm,c[i])*lcm;
            lcm%=k;
        }
        if(lcm==0)cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
        return 0;
}