hdu-5120 Intersection(计算几何)

题目链接：

Intersection

Time Limit: 4000/4000 MS (Java/Others)    

Memory Limit: 512000/512000 K (Java/Others)

Problem Description

 

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.


A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.


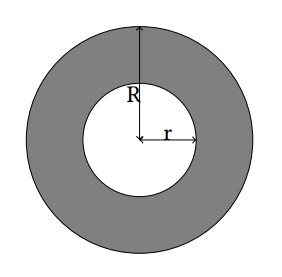
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

 

 

Input

 

The first line contains only one integer T (T ≤ 10⁵), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x_i, y_i (0 ≤ x_i, y_i ≤ 20) indicating the coordinates of the center of each ring.

 

 

Output

 

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

 

 

Sample Input

 

2

2 3

0 0

0 0

2 3

0 0

5 0

 

 

Sample Output

 

Case #1: 15.707963

Case #2: 2.250778

 

题意：

 

求两个圆环相交的面积;

 

思路：

 

ans=两个大圆的面积交+两个小圆的面积交-2*大圆与小圆的面积交;

 

AC代码：

 

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=1e5+6;
const LL mod=1e9+7;
const double PI=acos(-1.0);
double fun(double x,double y,double fx,double fy,double r,double R)
{
double    dis=sqrt((x-fx)*(x-fx)+(y-fy)*(y-fy));
    //cout<<dis<<endl;
        if(dis>=r+R)return 0;
        else if(dis<=R-r)
        {
            return PI*r*r;
        }
        else
        {
            double angle1,angle2,s1,s2,s3,s;
            angle1=acos((r*r+dis*dis-R*R)/(2*r*dis));
        angle2=acos((R*R+dis*dis-r*r)/(2*R*dis));

        s1=angle1*r*r;s2=angle2*R*R;
        s3=r*dis*sin(angle1);
        s=s1+s2-s3;
        return s;
        }
}
int main()
{
    int t;
    scanf("%d",&t);
    double r,R,x,y,fx,fy;
    int cnt=1;
    while(t--)
    {

        scanf("%lf%lf",&r,&R);
        scanf("%lf%lf%lf%lf",&x,&y,&fx,&fy);
        double ans1,ans2,ans3,ans4;
        ans1=fun(x,y,fx,fy,R,R);
        ans2=fun(x,y,fx,fy,r,r);
        ans3=fun(x,y,fx,fy,r,R);
        ans4=fun(fx,fy,x,y,r,R);
        printf("Case #%d: ",cnt++);
        printf("%.6lf\n",ans1+ans2-ans3-ans4);
    }

}