codeforces 659E E. New Reform(图论)

题目链接：

E. New Reform

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Berland has n cities connected by m bidirectional roads. No road connects a city to itself, and each pair of cities is connected by no more than one road. It is not guaranteed that you can get from any city to any other one, using only the existing roads.

The President of Berland decided to make changes to the road system and instructed the Ministry of Transport to make this reform. Now, each road should be unidirectional (only lead from one city to another).

In order not to cause great resentment among residents, the reform needs to be conducted so that there can be as few separate cities as possible. A city is considered separate, if no road leads into it, while it is allowed to have roads leading from this city.

Help the Ministry of Transport to find the minimum possible number of separate cities after the reform.

Input

The first line of the input contains two positive integers, n and m — the number of the cities and the number of roads in Berland (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000).

Next m lines contain the descriptions of the roads: the i-th road is determined by two distinct integers xi, yi (1 ≤ xi, yi ≤ n, xi ≠ yi), where xi and yi are the numbers of the cities connected by the i-th road.

It is guaranteed that there is no more than one road between each pair of cities, but it is not guaranteed that from any city you can get to any other one, using only roads.

Output

Print a single integer — the minimum number of separated cities after the reform.

Examples

input

4 3
2 1
1 3
4 3

output

1

input

5 5
2 1
1 3
2 3
2 5
4 3

output

0

input

6 5
1 2
2 3
4 5
4 6
5 6

output

1

Note

In the first sample the following road orientation is allowed: , , .

The second sample: , , , , .

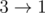The third sample: , , , , .

 

 题意:

 

给一个图的描述,注意有没有连接的点,把双向边变成单向边,问最后最少有多少个点没有边连向它;

 

思路：

贪心可以发现,没有连接的点首先就是,然后形成环的最后都能有边连向它们,然后就是像拓扑排序那样减入度,删边找到最后剩下的那些点;

 

AC代码：

 

/*
2014300227    659E - 36    GNU C++11    Accepted    78 ms    6668 KB
*/

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+4;
int n,m,x,y,flag[N],num[N],vis[N];
vector<int>ve[N];
queue<int>qu;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        ve[x].push_back(y);
        ve[y].push_back(x);
        num[x]++;
        num[y]++;
    }
    for(int i=1;i<=n;i++)
    {
         if(num[i]==1)
        {
            qu.push(i);
        }
    }
    while(!qu.empty())
    {
        int to=qu.front();
        vis[to]=1;
        qu.pop();
        if(num[to]){
            flag[to]=1;
            int len=ve[to].size(),b;
            for(int i=0;i<len;i++)
            {
                b=ve[to][i];
                if(!vis[b])
                {
                   num[b]--;
                   if(num[b]==1)
                    {
                        qu.push(b);
                    }
                    break;
                }
            }
        }
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(flag[i]==0&&num[i]==0)
        {
            ans++;
        }
    }
    cout<<ans<<"\n";

    return 0;
}