***1133. Fibonacci Sequence(斐波那契数列，二分，数论)

1133. Fibonacci Sequence

Time limit: 1.0 second
Memory limit: 64 MB
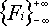
Problem illustration
is an infinite sequence of integers that satisfies to Fibonacci conditionFi + 2 = Fi + 1 + Fi for any integer i. Write a program, which calculates the value of Fn for the given values of Fi and Fj.

Input

The input contains five integers in the following order: i, Fi, j, Fj, n.
−1000 ≤ i, j, n ≤ 1000, i ≠ j,
−2·109 ≤ Fk ≤ 2·109 (k = min(i, j, n), …, max(i, j, n)).

Output

The output consists of a single integer, which is the value of Fn.

Sample

inputoutput
3 5 -1 4 5
 
12

 

 

 1 #include <iostream>
 2 using namespace std;
 3 const int oo=2000000001;
 4 int now;
 5 __int64 i,fi,j,fj,n;
 6 __int64 l=-oo,r=oo,mid,sum[3];
 7 int main()
 8 {
 9     cin >> i >> fi >> j >> fj >> n;
10     if (i > j)
11     {
12         swap(i,j);
13         swap(fi,fj);
14     }//进行调整，使得i比j考前
15     while (l <= r)
16     {//进行二分
17         mid=(l+r)>>1;//先取中间值，mid表示第i+1个数的值
18         sum[0]=fi;
19         sum[now=1]=mid;
20         int k=i+2,flag=-2;
21         while (k <= j)
22         {//计算加法运算次数
23             now=(now+1)%3;
24             ++k;
25             sum[now]=sum[(now+2)%3]+sum[(now+1)%3];
26             if (sum[now] > oo)  flag=1;//向上超界了用1进行标记
27             else if (sum[now] < (-oo))  flag=-1;//超出了最低限用-1进行标记
28             if (flag != -2)  break;//超界了就不需要在进行运算了
29         }
30         if (flag == -2)
31         {
32             if (sum[now] > fj)  flag=1;//没有超界但是大于fj表示mid开大了
33             else if (sum[now] < fj)  flag=-1;//没有超界但是运算到了j小于fj表示mid开小了
34             else  flag=0;//mid开正确了
35         }
36         if (flag == 1)  r=mid-1;//开大了重置r
37         else if (flag == -1)  l=mid+1;//开小了总之L
38         else if (flag == 0)  break;//正好则跳出
39     }
40     sum[0]=fi;
41     sum[now=1]=mid;//进行模拟找到第n个数
42     if (i < n)
43     {
44         int k=i+2;
45         while (k <= n)
46         {
47             now=(now+1)%3;
48             ++k;
49             sum[now]=sum[(now+2)%3]+sum[(now+1)%3];
50         }
51     }
52     else if (i > n)
53     {
54         int k=i-1;
55         while (k >= n)
56         {
57             now=(now+1)%3;
58             --k;
59             sum[now]=sum[(now+2)%3]-sum[(now+1)%3];
60         }
61     }
62     else  --now;
63     cout << sum[now] << endl;
64     return 0;
65 }
View Code

 

 

posted @ 2013-11-05 19:52  秋心无波  阅读(288)  评论(0)  编辑  收藏  举报