****Curling 2.0(深搜+回溯)
Curling 2.0
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 131072/65536K (Java/Other)
Total Submission(s) : 30 Accepted Submission(s) : 16
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
- At the beginning, the stone stands still at the start square.
- The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
- When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
- Once thrown, the stone keeps moving to the same direction until one of the following occurs:
- The stone hits a block (Fig. 2(b), (c)).
- The stone stops at the square next to the block it hit.
- The block disappears.
- The stone gets out of the board.
- The game ends in failure.
- The stone reaches the goal square.
- The stone stops there and the game ends in success.
- The stone hits a block (Fig. 2(b), (c)).
- You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.
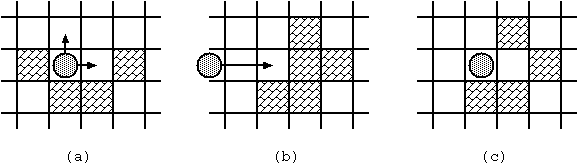
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
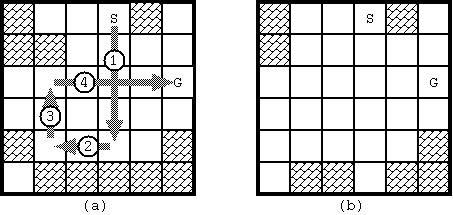
Fig. 3: The solution for Fig. D-1 and the final board configuration
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
题意:
就是要求把一个冰壶从起点“2”用最少的步数移动到终点“3”
其中0为移动区域,1为石头区域,冰壶一旦想着某个方向运动就不会停止,也不会改变方向(想想冰壶在冰上滑动),除非冰壶撞到石头1 或者 到达终点 3
注意的是:
冰壶撞到石头后,冰壶会停在石头前面,此时(静止状态)才允许改变冰壶的运动方向,而该块石头会破裂,石头所在的区域由1变为0. 也就是说,冰壶撞到石头后,并不会取代石头的位置。
终点是一个摩擦力很大的区域,冰壶若到达终点3,就会停止在终点的位置不再移动。
解题思路:
其实与其说这是深搜题,我觉得更像模拟题。。。
要先明确:
0为滑动区域
1为石头区域
2为起点,也是可滑动区域
3为终点,不可滑动区域
(1) 起点为“2”,也是一个可滑动的区域,所以标记起点位置之后,可以把起点当做0
(2) 注意区分冰壶是运动的还是静止的,若是静止的话,旁边1格有石头是不能走的。
(3) 输出冰壶从2到3的最短路,如果最短路的步数大于10(不包括10),视作无法走到终点(其实这是用来剪枝的)
(4) 滑动过程中冰壶不允许出界
基于上面的原则,不难发现:
(1)所谓的“走一步”,就是指冰壶从一个静止状态到下一个静止状态,就是说冰壶在运动时经过的“格数”不视作“步数”,也就是说冰壶每次移动的距离都是不定的。
(2)还有就是由于石头会因为冰壶的碰撞而消失,因此冰壶每“走一步”,场地的环境就会改变一次。
(3)基于(2),可以发现本题虽然是要找 “最短路”,但是BFS几乎不可能,因为每“走一步”,场地的状态就要改变一次;而如果该步不满足要求,又要求把场地的状态还原到前一步,这只有DFS能做到。
(4)基于(3),DFS不是BFS,不能简单地用它来找最短路,必须要把所有可能的路一一找出来,再逐一比较它们的步数才能确定最短。但题目值允许1000MS,此时就面临一个超时的问题。所以题目才同时给出“步数超过10则视为失败”的条件,这是用来剪枝的
有了上面的分析,就能最终确定本题的解法了:
有2种方法:
DFS+Vector+剪枝
DFS+回溯+剪枝
但是由于POJ对STL的“兼容性”很差,我用STL就没见过不TLE的题。。。这题也一样,所以不推荐,其实Vector是很好用的,利用它的特性可以在DFS返回上一步时,自动还原场地状态,而回溯法则需要手动还原场地状态(其实也就8行代码)
DFS用于寻找路径,回溯(或Vector)用于还原棋盘状态,剪枝用于优化
回溯:

1 #include<iostream> 2 using namespace std; 3 4 5 6 7 typedef class 8 { 9 public: 10 int r,c; //冰壶当前位置 11 bool status; //status冰壶当前状态:运动true ,静止false 12 }SE; 13 14 SE s,e; //记录冰壶起止点 15 int w,h; //场地size 16 int MinStep; //最短路 17 int board[30][30]; //场地 18 19 20 void DFS(int i,int j,bool status,int direction,int step,bool flag) 21 { //direction:冰壶当前运动方向 North:0 West:1 South:2 East:3 22 //flag:是否消除direction方向下一格位置的石头 23 24 if(step>10) //剪枝,超过10步的走法就不再考虑了 25 return; 26 if(board[i][j]==3) //终点 27 { 28 if(MinStep>step) 29 MinStep=step; 30 return; 31 } 32 33 if(flag) //消除石头 34 { 35 switch(direction) 36 { 37 case 0: {board[i-1][j]=0; break;} 38 case 1: {board[i][j-1]=0; break;} 39 case 2: {board[i+1][j]=0; break;} 40 case 3: {board[i][j+1]=0; break;} 41 } 42 } 43 44 if(!status) //静止 45 { 46 if(i-1>=1 && (board[i-1][j]==0 || board[i-1][j]==3)) //上 47 DFS(i-1,j,true,0,step+1,false); 48 49 if(j-1>=1 && (board[i][j-1]==0 || board[i][j-1]==3)) //左 50 DFS(i,j-1,true,1,step+1,false); 51 52 if(i+1<=h && (board[i+1][j]==0 || board[i+1][j]==3)) //下 53 DFS(i+1,j,true,2,step+1,false); 54 55 if(j+1<=w && (board[i][j+1]==0 || board[i][j+1]==3)) //右 56 DFS(i,j-1,true,3,step+1,false); 57 } 58 else //运动 59 { 60 switch(direction) 61 { 62 case 0: 63 { 64 if(i-1<1) //预判下一步是否越界 ,越界的话深搜停止 65 return; 66 else 67 { 68 if(board[i-1][j]==0) //下一位置为0且不越界,继续运动 69 DFS(i-1,j,true,0,step,false); 70 else if(board[i-1][j]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 71 DFS(i,j,false,0,step,true); 72 else if(board[i-1][j]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 73 DFS(i-1,j,false,0,step,false); 74 } 75 break; 76 } 77 case 1: 78 { 79 if(j-1<1) //预判下一步是否越界 80 return; 81 else 82 { 83 if(board[i][j-1]==0) //下一位置为0且不越界,继续运动 84 DFS(i,j-1,true,1,step,false); 85 else if(board[i][j-1]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 86 DFS(i,j,false,1,step,true); 87 else if(board[i][j-1]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 88 DFS(i,j-1,false,1,step,false); 89 } 90 91 break; 92 } 93 case 2: 94 { 95 if(i+1>h) //预判下一步是否越界 96 return; 97 else 98 { 99 if(board[i+1][j]==0) //下一位置为0且不越界,继续运动 100 DFS(i+1,j,true,2,step,false); 101 else if(board[i+1][j]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 102 DFS(i,j,false,2,step,true); 103 else if(board[i+1][j]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 104 DFS(i+1,j,false,2,step,false); 105 } 106 107 break; 108 } 109 case 3: 110 { 111 if(j+1>w) //预判下一步是否越界 112 return; 113 else 114 { 115 if(board[i][j+1]==0) //下一位置为0且不越界,继续运动 116 DFS(i,j+1,true,3,step,false); 117 else if(board[i][j+1]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 118 DFS(i,j,false,3,step,true); 119 else if(board[i][j+1]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 120 DFS(i,j+1,false,3,step,false); 121 } 122 break; 123 } 124 } 125 } 126 127 if(flag) //回溯前还原石头,即还原上一步的棋盘状态 128 { 129 switch(direction) 130 { 131 case 0: {board[i-1][j]=1; break;} 132 case 1: {board[i][j-1]=1; break;} 133 case 2: {board[i+1][j]=1; break;} 134 case 3: {board[i][j+1]=1; break;} 135 } 136 } 137 return; 138 } 139 140 int main(void) 141 { 142 while(cin>>w>>h) 143 { 144 if(!w && !h) 145 break; 146 MinStep=11; 147 for(int i=1;i<=h;i++) 148 for(int j=1;j<=w;j++) 149 { 150 cin>>board[i][j]; 151 if(board[i][j]==2) 152 { 153 s.r=i; 154 s.c=j; 155 s.status=false; 156 board[i][j]=0; //记录起点位置后,把它作为0处理 157 } 158 if(board[i][j]==3) //终点是特别位置,冰壶经过或到达该格都会停止 159 { 160 e.r=i; 161 e.c=j; 162 } 163 } 164 DFS(s.r , s.c , s.status , 0 , 0 , false); 165 166 if(MinStep<=10) 167 cout<<MinStep<<endl; //DFS里面虽然剪枝了,但是可能把全部走法都剪了,因此还是要判断 168 else 169 cout<<-1<<endl; 170 } 171 return 0; 172 }
Vector:

1 #include<iostream> 2 #include<vector> 3 using namespace std; 4 5 const int inf=11; 6 7 typedef class 8 { 9 public: 10 int r,c; //冰壶当前位置 11 bool status; //status冰壶当前状态:运动true ,静止false 12 }SE; 13 14 SE s,e; //记录冰壶起止点 15 int w,h; //场地size 16 int MinStep; //最短路 17 18 void DFS(vector<vector<int> >board,int i,int j,bool status,int direction,int step,bool flag) 19 { //direction:冰壶当前运动方向 North:0 West:1 South:2 East:3 20 //flag:是否消除direction方向下一格位置的石头 21 22 if(step>10) //剪枝,超过10步的走法就不再考虑了 23 return; 24 25 if(board[i][j]==3) //终点 26 { 27 if(MinStep>step) 28 MinStep=step; 29 return; 30 } 31 32 if(flag) //消除石头 33 { 34 switch(direction) 35 { 36 case 0: {board[i-1][j]=0; break;} //board用vector表示的目的就是为了在当前步删除某位置的石头时 37 case 1: {board[i][j-1]=0; break;} //前一步并不会删除该位置的石头 38 case 2: {board[i+1][j]=0; break;} 39 case 3: {board[i][j+1]=0; break;} 40 } 41 } 42 43 if(!status) //静止 44 { 45 if(i-1>=1 && (board[i-1][j]==0 || board[i-1][j]==3)) //North 46 DFS(board,i-1,j,true,0,step+1,false); 47 48 if(j-1>=1 && (board[i][j-1]==0 || board[i][j-1]==3)) //West 49 DFS(board,i,j-1,true,1,step+1,false); 50 51 if(i+1<=h && (board[i+1][j]==0 || board[i+1][j]==3)) //South 52 DFS(board,i+1,j,true,2,step+1,false); 53 54 if(j+1<=w && (board[i][j+1]==0 || board[i][j+1]==3)) //East 55 DFS(board,i,j-1,true,3,step+1,false); 56 } 57 else if(status) //运动 58 { 59 switch(direction) 60 { 61 case 0: 62 { 63 if(i-1<1) //预判下一步是否越界 64 return; 65 else 66 { 67 if(board[i-1][j]==0) //下一位置为0且不越界,继续运动 68 DFS(board,i-1,j,true,0,step,false); 69 else if(board[i-1][j]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 70 DFS(board,i,j,false,0,step,true); 71 else if(board[i-1][j]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 72 DFS(board,i-1,j,false,0,step,false); 73 } 74 75 break; 76 } 77 case 1: 78 { 79 if(j-1<1) //预判下一步是否越界 80 return; 81 else 82 { 83 if(board[i][j-1]==0) //下一位置为0且不越界,继续运动 84 DFS(board,i,j-1,true,1,step,false); 85 else if(board[i][j-1]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 86 DFS(board,i,j,false,1,step,true); 87 else if(board[i][j-1]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 88 DFS(board,i,j-1,false,1,step,false); 89 } 90 91 break; 92 } 93 case 2: 94 { 95 if(i+1>h) //预判下一步是否越界 96 return; 97 else 98 { 99 if(board[i+1][j]==0) //下一位置为0且不越界,继续运动 100 DFS(board,i+1,j,true,2,step,false); 101 else if(board[i+1][j]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 102 DFS(board,i,j,false,2,step,true); 103 else if(board[i+1][j]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 104 DFS(board,i+1,j,false,2,step,false); 105 } 106 107 break; 108 } 109 case 3: 110 { 111 if(j+1>w) //预判下一步是否越界 112 return; 113 else 114 { 115 if(board[i][j+1]==0) //下一位置为0且不越界,继续运动 116 DFS(board,i,j+1,true,3,step,false); 117 else if(board[i][j+1]==1) //下一位置为1且不越界,停止运动,并消除下一位置的石头 118 DFS(board,i,j,false,3,step,true); 119 else if(board[i][j+1]==3) //下一位置为3且不越界,运动到位置3后停止运动,游戏结束 120 DFS(board,i,j+1,false,3,step,false); 121 } 122 123 break; 124 } 125 } 126 } 127 128 return; 129 } 130 131 int main(void) 132 { 133 while(cin>>w>>h) 134 { 135 if(!w && !h) 136 break; 137 138 /*Structure the Board*/ 139 140 MinStep=inf; 141 vector<vector<int> >board(h+1,vector<int>(w+1)); 142 143 for(int i=1;i<=h;i++) 144 for(int j=1;j<=w;j++) 145 { 146 cin>>board[i][j]; 147 148 if(board[i][j]==2) 149 { 150 s.r=i; 151 s.c=j; 152 s.status=false; 153 board[i][j]=0; //记录起点位置后,把它作为0处理 154 } 155 if(board[i][j]==3) //终点是特别位置,冰壶经过或到达该格都会停止 156 { 157 e.r=i; 158 e.c=j; 159 } 160 } 161 162 /*Search the min path*/ 163 164 DFS(board , s.r , s.c , s.status , 0 , 0 , false); 165 166 if(MinStep<=10) 167 cout<<MinStep<<endl; //DFS里面虽然剪枝了,但是可能把全部走法都剪了,因此还是要判断 168 else 169 cout<<-1<<endl; 170 171 /*Relax*/ 172 173 // board.swap(vector<vector<int> >()); //POJ好像禁用swap() 174 } 175 return 0; 176 }





