用FFM做召回

特征表示

	Field	feature	feature取值	x	备注
user侧	Field1	性别	男	x1	每个取值对应一个x
			女	x2
	Field2	年龄	<18	x3	连续特征先离散化
			19-24	x4
			25-30	x5
			31-35	x6
			36-40	x7
			>40	x8
	Field3	省	山西	x9
			广西	x10
			陕西	x11
			...	....
		城市	洛阳	x300	可能的取值很多， 一个样本只会命 中一个取值
			安阳	x301
			南阳	x302
			...	...
item侧	Field4	关键词	足球	x1000	一个样本会同时命 中多个
			5G	x1001
			...	...
	Field5	时效性	3小时	x5000
			当天	x5001
			7天	x5002
			永久	x5003

这个例子中，一共有5个域，6个特征，5003个x，但对于一样本“最多”只有$5+l$个x是1，其它x全是0，$l$表示item关键词的个数，之所以说“最多”是因为一个样本的某些特征可能取不到，对应的x就全是0。

FFM公式变换

$$\hat{y}=\sum_{i=1}^nw_ix_i+\sum_{k=1}^K\sum_{i=1}^n\sum_{j=i+1}^nV_{i,fj,k}V_{j,fi,k}x_ix_j$$ 

$x$非0即1，所以乘上$x$实际上是对$w$和$V$进行挑选。$V$是一个size为$n\times F \times K$的三维矩阵，$n$是x的个数，在表一中$n=5003$，F是域的个数，在表一中F=5，$V_{i,fj}是$x_i$去跟$Field_j$交叉时使用的向量，$K是向量的长度，通常取4、8、16。

上式的第一项对所有的$w$求和，这没什么好说的，我们重点关注第二项的形式变换。第二项最外层按$k$求和也变不出什么花样，在$k$取某一个具体值的情况下我们看看$\sum_{i=1}^n\sum_{j=i+1}^nV_{i,fj}V_{j,fi}$如何做形式变换。这要分成两种情况来看待：$i$和$j$是否属于同一个Field。

$i$和$j$属于不同的Field

试想属于同一个Field的$x$下标都是连续的，当$i$和$j$属于不同的Field时

$$\sum_{i=1}^n\sum_{j=i+1}^nV_{i,fj}V_{j,fi}=\sum_{p=1}^F\sum_{q=p+1}^F\sum_{i\in Filed_p}\sum_{j\in Filed_q}V_{i,q}V_{j,p}=\sum_{p=1}^F\sum_{q=p+1}^F\sum_{i\in Filed_p}V_{i,q}\sum_{j\in Filed_q}V_{j,p}$$

令$F_{p,q}=\sum_{i\in Filed_p}V_{i,q}$，它表示$Field_p$内部的所有$x$跟$Field_q$交叉时使用的向量按位相加之和。

举个例子，比如$a$、$b$、$c$属于Field1，$d$、$e$属于Field2，则$ad+ae+bd+de+cd+ce=(a+b+c)(d+e)$。只需要一次乘法。

$i$和$j$属于同一个Field

当$i$和$j$属于同一个Field时

\begin{eqnarray*} \begin{aligned} \sum_{i=1}^n\sum_{j=i+1}^nV_{i,fj}V_{j,fi}=\sum_{f=1}^F\sum_{i=1}\sum_{j=i+1}V_{i,f}V_{j,f}&=\sum_{f=1}^F\frac{1}{2}\left[\sum_{i=1}\sum_{j=1}V_{i,f}V_{j,f}-\sum_{i=1}V_{i,f}^2\right]\\ &=\sum_{f=1}^F\frac{1}{2}\left[\sum_{i=1}V_{i,f}\sum_{j=1}V_{j,f}-\sum_{i=1}V_{i,f}^2\right]\\ &=\sum_{f=1}^F\frac{1}{2}\left[\left(\sum_{i=1}V_{i,f}\right)^2-\sum_{i=1}V_{i,f}^2\right] \end{aligned} \end{eqnarray*}

解释一下第一行的变换是怎么来的，试想一个对称方阵上角元素之和等于方阵所有元素之和减去对角线元素之和，再除以2。

举个例子，比如$a$、$b$、$c$属于同一个Fied，则$ab+ac+bc=\frac{1}{2}[(a+b+c)^2-(a^2+b^2+c^2)]$。乘法计算量由$O(n^2)$ 降为$O(n)$，$n$表示该Field内有几个特征。

user和item的向量表示

 给一个user推荐一批item，FFM决策函数里只跟user特征相关的项可以去掉，不影响item的排序，这包括$\sum_{x_i \in UserFeature}w_ix_i$以及$\sum_{i=1}^n\sum_{j=i+1}^n\vec{V}_{i,fj}\cdot\vec{V}_{j,fi}x_ix_j$中$x_i$和$x_j$同时属于UserFeature的情况。

对应地，只跟item特征相关的项全部加起来，构成ItemBias。即

$$ItemBias=\sum_{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^n\vec{V}_{i,fj}\cdot\vec{V}_{j,fi}x_ix_j\qquad x_i \in ItemFeature\ \text{且}\  x_j \in ItemFeature$$

 

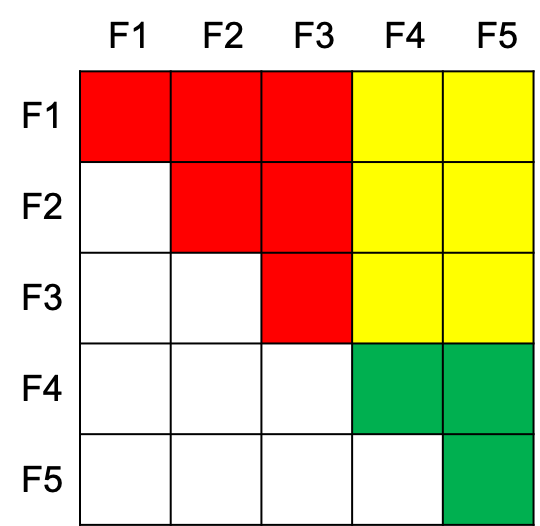
用这个图来理解FFM的二次项，设Field1、2、3是user侧的，Field4、5是item侧的。Field1、2、3域之间的交叉以及每个域内部各特征之间的交叉是红色区域，这一块属于UserBias，可以丢弃掉不影响item的排序。绿色区域属于ItemBias。黄色区域是UserFeature和ItemFeature之间的交叉，它相当于

\begin{equation}F_{1,4}F_{4,1}+F_{1,5}F_{5,1}+F_{2,4}F_{4,2}+F_{2,5}F_{5,2}+F_{3,4}F_{4,3}+F_{3,5}F_{5,3}\label{cross}\end{equation}

下三角白色区域是不需要交叉的，因为在FFM的二次项里j是从i+1开始的，推出$Field_p$和$Field_q$交叉时只需要计算$q>p$的情况。图中的对角线也标上了颜色，并不是说一个域需要自己跟交叉，而是说一个域内部各特征之间还需要交叉。

把$[F_{1,4},F_{1,5},F_{2,4},F_{2,5},F_{3,4},F_{3,5}]$首尾相连拼接成User向量，把$[F_{4,1},F_{5,1},F_{4,2},F_{5,2},F_{4,3},F_{5,3}]$首尾相连拼接成Item向量，则(\ref{cross})式等于User向量和Item向量的内积。

为了把ItemBias加进来，需要在User向量最后补一个1，同时在Item向量最后补一个ItemBias。

再次明确一下ItemBias包含三部分：

\begin{matrix}\sum_{i=1}^nw_ix_i & x_i \in ItemFeature \\\sum_{f\in ItemField}\sum_{i=1}\sum_{j=i+1}\vec{V}_{i,f}\cdot\vec{V}_{j,f} & x_i \in Field_f\textrm{且} x_j \in Field_f,\textrm{即同一个Field内部各特征做交叉}\\\sum_p\sum_{q=p+1}F_{p,q}\cdot F_{q,p} & p\in ItemField\textrm{且}q\in ItemField, \text{即item侧Field之间两两交叉}\end{matrix}

寻找向量的最近邻

KD Tree维度小于20时效率最高，随着维度的增加效率会迅速下降，所以就有了Ball Tree。

Faiss通过PCA和PQ(乘积量化)对向量进行压缩和编码。

 

最后再附上我做的PPT: FM和FFM召回算法