神经网络调优

Michael Nielsen在他的在线教程《neural networks and deep learning》中讲得非常浅显和仔细，没有任何数据挖掘基础的人也能掌握神经网络。英文教程很长，我捡些要点翻译一下。

交叉熵损失函数

回顾一下上篇的公式(7)和(8)，基于最小平方误差（MSE）的缺失函数对w和b求导时，都包含一个因子$\delta=\frac{\partial C}{\partial z}=\frac{\partial C}{\partial a}\sigma'(z)=(a-y)\sigma'(z)$，可见学习率取决于$(a-y)$和$\sigma'(z)$的乘积。$a$和$y$的差距越大学习率就越大这是应该的，可是$\sigma'(z)$很容易接近于0，因为sigmoid函数在绝大部分定义域上都位于饱和区（或称平坦区），这就会导致神经网络学习得很慢。所以要寻找一个新的损失函数，使得梯度中没有$\sigma'(z)$这项因子，于是就找到了交叉熵损失函数。

\begin{equation}C\equiv-[ylna+(1-y)ln(1-a)], a=\sigma(z)\label{ce}\end{equation}

当然作为损失函数，交叉熵具有2个性质：1.非负；2.$a$与$y$相差越多交叉熵就越大。

我们来算一下基于交叉熵损失函数和sigmoid激活函数的梯度是多少。

\begin{equation}\delta=\frac{\partial C}{\partial z}=\frac{\partial C}{\partial a}\sigma'(z)=-\frac{y}{a}\sigma'(z)+\frac{1-y}{1-a}\sigma'(z)=\frac{a-y}{a(1-a)}\sigma'(z)=a-y\label{pc}\end{equation}

最后一步推导时用到了《什么是神经网络》中的公式(5)。

输出值$a$和真实值$y$差距得越大，学习率就越大，避免了学习率趋于0的问题。所以通常情况下，当激活函数选用sigmoid时，损失函数选用交叉熵比用最小平方误差要好。

softmax

在深度学习算法中最后一层经常使用softmax函数替代sigmoid函数。最后一层的输入依然是$z^L_j = \sum_{k} w^L_{jk} a^{L-1}_k + b^L_j$，softmax激活函数为

$$a^L_j = \frac{e^{z^L_j}}{\sum_k e^{z^L_k}}$$

上标$L$表示第$L$层，即最后一层。下标$j$表示该层上的第$j$个神经元。$a$是神经元的输出。

最后一层神经元的输出形成一个概率分布，即

$$\sum_j a^L_j  =  \frac{\sum_j e^{z^L_j}}{\sum_k e^{z^L_k}} = 1$$

在上篇的手写数字识别试验中，最后一层采用sigmoid激活函数时我们可以取输出值最大的那个神经元来判断数字是几，但是并不知道这张图片是各个数字的概率，而softmax函数的输出$a^L_j$本身就表示是数字$j$的概率，或者说在多分类问题中$a^L_j$表示样本属于第$j$个类别的概率。

当采用softmax时，损失函数须采用似然函数的相反数方能避免学习率慢的问题。样本属于第j类的似然函数是$a^L_j$，极大似然估计就是令目标函数为$max\;a^L_j$，即$max\; \ln a^L_j$。

损失函数为$C \equiv -\ln a^L_j$，即$C \equiv \ln \left(\sum_k{e^{z^L_k}}\right) - z^L_j$

对w和b求导

$$\frac{\partial C}{\partial b^L_i}=\frac{e^{z^L_i}}{\sum_k e^{z^L_k}}\frac{\partial z^L_i}{\partial b^L_i}-\frac{\partial z^L_j}{\partial b^L_i}=a^L_i-\frac{\partial z^L_j}{\partial b^L_i}$$

$$\frac{\partial C}{\partial b^L_i}=\left\{\begin{matrix}a^L_i & if \; i\ne j \\ a^L_i-1.0 & if \; i=j\end{matrix}\right.$$

同理

$$\frac{\partial C}{\partial w^L_{ik}}=a^L_ia^{L-1}_k-\frac{\partial z^L_j}{\partial w^L_{ik}}$$

$$\frac{\partial C}{\partial w^L_{ik}}=\left\{\begin{matrix}a^L_ia^{L-1}_k & if \; i\ne j \\ a^{L-1}_k(a^L_i-1.0) & if \; i=j\end{matrix}\right.$$

sigmoid结合交叉熵损失函数用，softmax结合对数似然函数用，都可以避免学习率慢的问题。

网络参数的初始化

给w和b初始化时，尽量赋的值小一些，这样$z=wx+b$就会比较小，$z$比较小有2个好处：

1. $\sigma(z)$离1和0都比较近，给两种结果都留有充分的可能性
2. $\sigma(z)$函数不在饱和区，学习率比较大（如果采用MSE的话）

比如我们可以让初始的$w \sim N(0,1), b \sim N(0,1)$。假如输入层有m个神经元的输出为1，其他神经元的输出均为0，则$z=wx+b$是m个相互独立的标准正态随机变量的和，所以$z \sim N(0,\sqrt{m})$，即$z$的方差是$m$个$w$的方差之和。当$m$很大时$z$的方差就很大，$\sigma(z)$还是会有很大的概率落入饱和区。如果要使$z$的方差比较小，那$w$的方差就需要更小，比如要想使$z$的方差为1，那$w$的方差就需要是$\frac{1}{m}$，即$w \sim N(0,\frac{1}{\sqrt{m}})$。

注：X和Y都是正态随机变量，则X+Y也是正态随机变量，且均值为E(X)+E(Y)，方差为Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)，当X和Y相互独立时Cov(X,Y)=0。

过拟合

所谓过拟合就是模型太看重每一个训练样本了，导致模型在测试集上精度不佳，即模型的泛化能力不好。至少有2种方式会致使模型太看重训练样本，过度追求在训练集上的高精度：

1. 学习出一个很复杂的模型。
   
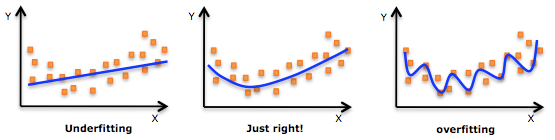
   第一张图是欠拟合，模型太过简单，在训练集上的精度低，在测试集上精度也低。
   第二张图得到的模型刚好，在训练集和测试集上的精度都比较高。
   第三图就是过拟合了，这条曲线代表的函数可能是一个非常高次的多项式函数，函数中需要有很多参数。这个函数虽然在训练集上精度非常高，但是在测试集上精度反而很低。
   奥卡姆剃刀原理告诉我们简单的模型更能揭示事物的本质，具有更好的泛化能力。
2. 设置一个很大的迭代次数。
   从大的趋势上看，随着迭代次数的增加，模型在训练集上的误差会越来越小。如下图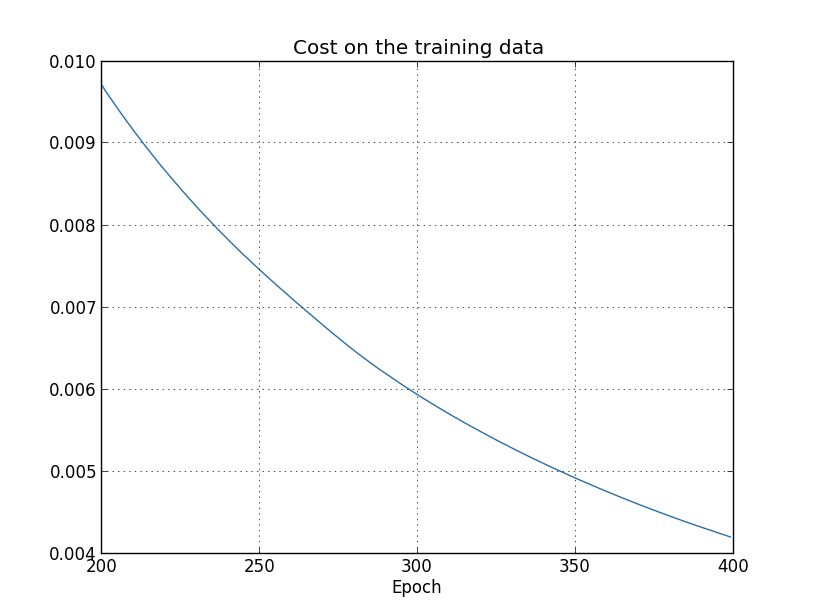
   
   但是在测试集上的精度可能从第300代开始就不再上升了。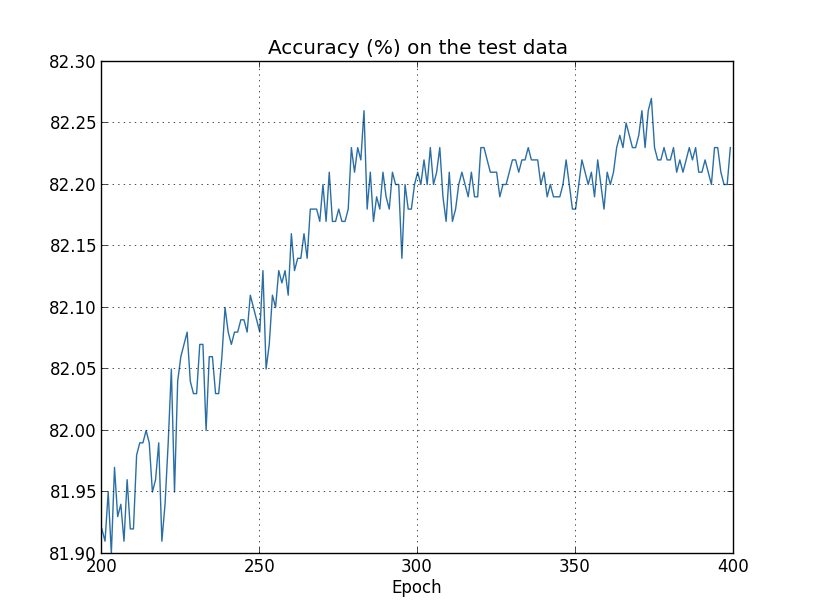
   
   甚至在测试集上误差呈现先下降后上升的趋势。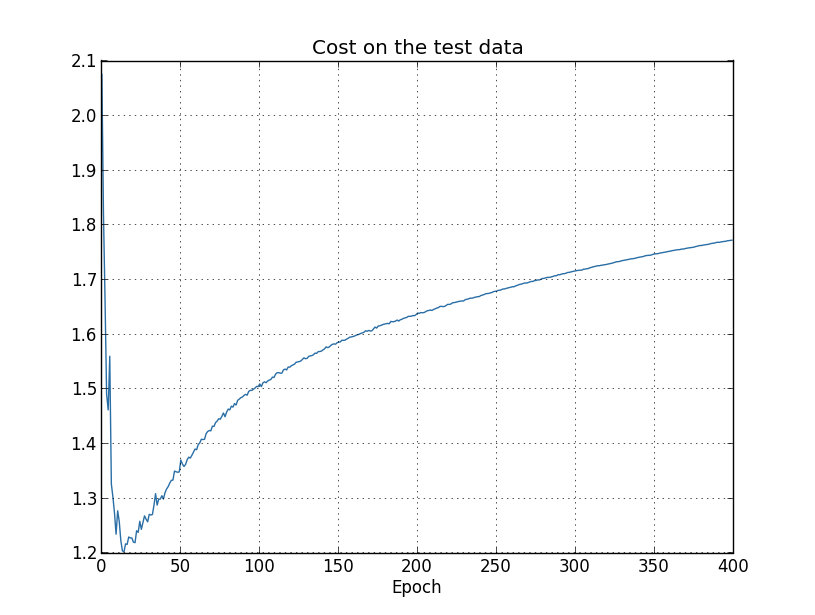
   
   那训练迭代多少代才合适呢？通常我们会把全部语料分成3个互不相交的子集：TrainSet, ValidationSet, TestSet。训练时每迭代一次，就拿当前的模型去ValidationSet上作预测，如果连续N代（N通常比较小，比如10）在ValidationSet上的精度都不再上升那迭代就可以停止了。

在计算资源允许的情况下，尽可能地增加样本数量可以提高模型的泛化能力，使这在测试集上取得更高的预测精度。在训练样本有限的情况下，我们如何得到更多的样本呢？在图像识别领域，可以把样本图片旋转/扭曲一个较小的角度再放回训练样集中。在语音识别领域，可以调快语速或者加点背影噪声再放回训练样本集中。

正则化

在神经网络中，$w$比较小的话，不会因为$x$的较小变动导致输出的较大变化，即对噪声的容忍程度比较好。换句话说，对于$wx$这样的线性变换，矩阵$w$的条件数越小，数值稳定性越好，而条件数$cond(w)=||w|| \cdot ||w^{-1}||$，即范数（不论是几范数）越小数值稳定性越好，这套理论详见我之前写的《矩阵计算》。基于此，L1正则和L2正则都是使$w$尽可能得小。$b$是否参与正则化关系不大，因为$b$不与$x$相乘，不存在对噪声敏感的问题，通常正则项中都只包含$w$不包含$b$。

未经正则化的神经网络对可能对噪声很敏感，相信大家都有一个共识：对噪声敏感的模型容易过拟合。所以正则化可以起到防止过拟合的作用。

L2正则

$$C=C_0+\frac{\lambda}{n}\sum_{i=1}^n{w_i^2}$$

$C_0$是正则化之前的损失函数，$\lambda$是正则项系数，$n$是参数$w$的个数。最小化损失函数$C$的同时也会使$\sum_{i=1}^n{w_i^2}$尽可能小。

加上正则项后梯度变为

$$\frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda}{2n}w$$

\begin{equation}w\to w'=w-\eta\frac{\partial C}{\partial w}=\left(1-\frac{\eta\lambda}{n}\right)w-\eta\frac{\partial C_0}{\partial w}\label{g1}\end{equation}

$\eta$是学习率。没有正则项时

\begin{equation}w\to w'=w-\eta\frac{\partial C_0}{\partial w}\label{g0}\end{equation}

对比式(\ref{g0})和式(\ref{g1})可知，L2正则项的作用是使$w$在每次迭代时都变小了$\frac{\eta\lambda}{n}$倍。如果要使这个倍率不变，那么当神经元个数增多（即$n$变大）时，正则项系数$\lambda$也应该相应调大。

L1正则

$$C=C_0+\frac{\lambda}{n}\sum_{i=1}^n{|w_i|}$$

$$\frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda}{n}sgn(w)$$

$sgn$是符号函数

$$sgn(w)=\left\{\begin{matrix}1 & if\;w\ge 0\\0 & if\;w<0\end{matrix}\right.$$

$$w \to w-\frac{\eta\lambda}{n}sgn(w)-\eta\frac{\partial C_0}{\partial w}=w\pm\frac{\eta\lambda}{n}-\eta\frac{\partial C_0}{\partial w}$$

所以L1正则的作用是使$w$在每一次迭代时都减小（也可能是增大，这取决于$sgn(w)$）一个常数：$\frac{\eta\lambda}{n}$。

当$w$本身比较小时，L1正则比L2正则衰减得更狠。L1正则的效果是使不重要的$w$几乎衰减为0。

dropout

试想训练多个神经网络让它们共同表决，比只训练一个神经网络更靠谱，因为每个神经网络都以不同的方式过拟合，取它们的平均值可以降低过拟合。dropout就是利用这种思想降低过拟合的，每次迭代时都随机地从隐藏层上去除一部分神经元，每个神经元都随机地与其他神经元进行组合，减小彼此之间的相互影响。dropout在大型深层网络中特别有用。

超参调优

神经网络隐藏层的个数、学习率$\eta$、正则项系数$\lambda$这些都属于超参数。超参数设为多少神经网络表现最佳呢？这个得试！“网格搜索”就是一种穷举尝试的方法，它事先给每个超参数设置几个需要尝试的值，然后得到所有超参数取各个值的任意组合情况，对于每种组合都去训练一个模型出来。显然这种方法的计算量是巨大的！在实际中我们会做2点简化：1.调试超参数时使用的训练集小一些。2.先调试重要性高的超参数（超参数的重要性怎么定？凭经验和感觉！），得到一个最佳限值后再去调试其他超参数。

数值优化方法

上篇的公式(5)是说每次迭代都需要把所有样本输给神经网络，所有样本一起决定参数该如何调整，这种方法参数调整得太慢。

与之相对的随机梯度下降法SGD，即每次迭代只随机选取1个样本，基于这1个样本的残差来调整模型参数。

折中的办法就是mini-batch法，每次迭代只取一小批样本，这样有2个好处：1.参数调整得不至于太慢。2.参数的更新都是矩阵运算，可以充分利用numpy中矩阵并行运算的优势。

关于数值优化当然还有其他很多方法。牛顿法比梯度下降法会更快地逼近最优解，还有动量法、Nestrov加速法、Adagrad法等等，详情请看我之前写的《优化方法》。

梯度不稳定

在深度学习中，梯度不稳定是一个大问题，所谓梯度不稳定是指不同神经元的梯度差异非常大，这表现在2个方面：

1. 梯度消失。越靠前的隐藏层，其学习率越小。
2. 梯度爆炸。越靠前的隐藏层，其学习率越大。

为什么会出现这种情况。举一个最简单的4层神经网络的例子，如下图

依照上篇的公式(11)和(12)有

$$\frac{\partial C}{\partial b_1}=\sigma'(z_1)w_2\sigma'(z_2)w_3\sigma'(z_3)w_4\sigma'(z_4)\frac{\partial C}{\partial a_4}$$

通常$w<1$，且$\sigma'(z)<0.25$【因为$\sigma'(z)=\sigma(z)(1-\sigma(z))$】，所以越往前梯度越小。

如果很不巧，每一层的$w$都很大的话，那么越往前梯度就越大。

使用tanh作激活函数同样会出现gradient vanish和gradient explod问题。在图像识别领域，有人使用修正的线性激活函数以及其变体：

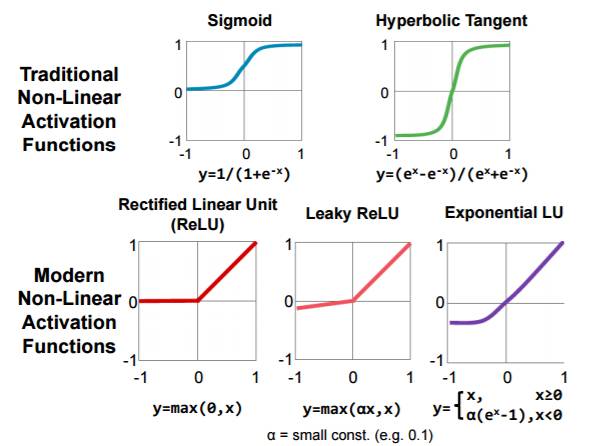
循环神经网络RNN常用于序列挖掘，比如语音识别，在RNN中vanishing gradient问题更加严重，于是引入了LSTM(Long Short-Term Memory ) 神经元到RNN中。