2021-03-04
作者:董鑫
链接:https://www.zhihu.com/question/66200879/answer/870023448
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
自动求导 (Automatic Differentiation, AD) 的课程 (CS207),正好来回答一下。 其实不只是 TensorFlow,Pytorch 这些为深度学习设计的库用到 AD,很多物理,化学等基础科学计算软件也在大量的使用 AD。而且,其实TensorFlow、Pytorch 也并非只能用于deep learning,本质上他们是一种
Tensor computation built on a tape-based autograd system --引自Pytorch
自动求导分成两种模式,一种是 Forward Mode,另外一种是 Reverse Mode。一般的机器学习库用的后一种,原因后面说。
Forward Mode
基于的就是就基本的 链式法则 chain rule,
![[公式]](https://www.zhihu.com/equation?tex=%5Cbegin%7Balign%7D+++%5Cnabla_%7Bx%7Dh+%3D+%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%7B%5Cfrac%7B%5Cpartial+h%7D%7B%5Cpartial+y_%7Bi%7D%7D%5Cnabla+y_%7Bi%7D%5Cleft%28x%5Cright%29%7D.+%5Cend%7Balign%7D+)
这个 Forward Mode 就是用 chain rule,像剥洋葱一样一层一层算出来
以
![[公式]](https://www.zhihu.com/equation?tex=+f%5Cleft%28x%5Cright%29+%3D+x+-+%5Cexp%5Cleft%28-2%5Csin%5E%7B2%7D%5Cleft%284x%5Cright%29%5Cright%29.++)
为例。 我们可以把他的计算图画出来。
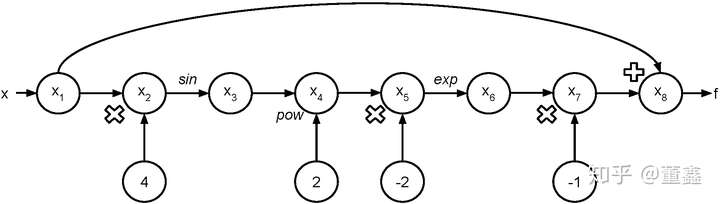
假如我要 计算 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28%5Cfrac%5Cpi%7B16%7D%29) ,可以根据上面的图得到一个表格
,可以根据上面的图得到一个表格
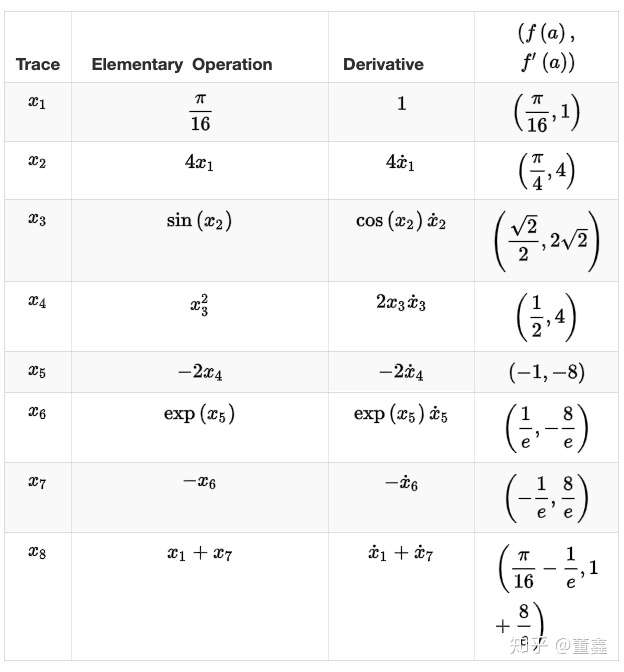
那么上面这个表里,每一步我们既要算 forward 的值 ![[公式]](https://www.zhihu.com/equation?tex=f%28a%29) ,也要算 backward 的值
,也要算 backward 的值 ![[公式]](https://www.zhihu.com/equation?tex=f%27%28a%29) 。
。
有没有办法同时把这两个值算出来呢?
首先引入一个新的概念,二元数。二元数其实跟复数差不多,也是一种实数的推广。我们回忆一下,一个复数可以写成这样的形式:
![[公式]](https://www.zhihu.com/equation?tex=+%5Cbegin%7Balign%7D+z+%3D+a+%2B+ib+%5C+i%5E2%3D-1+%5Cend%7Balign%7D+)
对于复数的理解,一个比较直观的例子就是。本来实数都是在一个实数轴(x轴)的。复部 ![[公式]](https://www.zhihu.com/equation?tex=ib) 相当于多了一个 y 轴出来。
相当于多了一个 y 轴出来。
那么二元数是这个亚子,
![[公式]](https://www.zhihu.com/equation?tex=%5Cbegin%7Balign%7D+z+%3D+a+%2B+%5Cepsilon+b+%5C+%5Cepsilon%5E2%3D0+%5Cend%7Balign%7D+)
这个二元数很神奇的一个性质是,你带着他做运算,得出来的二元部 ![[公式]](https://www.zhihu.com/equation?tex=%5Cepsilon+b) 前面的系数,就是导数。举个栗子, 我们要求
前面的系数,就是导数。举个栗子, 我们要求
![[公式]](https://www.zhihu.com/equation?tex=y%3D%5Csin%28x%29)
我们可以把 ![[公式]](https://www.zhihu.com/equation?tex=x%3Da%2B%5Cepsilon+b) ,所以
,所以
![[公式]](https://www.zhihu.com/equation?tex=+%5Cbegin%7Balign%7D++++y+%26+%3D+%5Csin%5Cleft%28a+%2B+%5Cepsilon+b%5Cright%29++%5C%5C+++++%26+%3D+%5Csin%5Cleft%28a%5Cright%29%5Ccos%5Cleft%28%5Cepsilon+b%5Cright%29+%2B+%5Ccos%5Cleft%28a%5Cright%29%5Csin%5Cleft%28%5Cepsilon+b%5Cright%29.++%5Cend%7Balign%7D+)
我们把上面的三角函数展开,
![[公式]](https://www.zhihu.com/equation?tex=+%5Cbegin%7Balign%7D+++%5Csin%5Cleft%28%5Cepsilon+b%5Cright%29+%26%3D+%5Csum_%7Bn%3D0%7D%5E%7B%5Cinfty%7D%7B%5Cleft%28-1%5Cright%29%5E%7Bn%7D%5Cdfrac%7B%5Cleft%28%5Cepsilon+b%5Cright%29%5E%7B2n%2B1%7D%7D%7B%5Cleft%282n%2B1%5Cright%29%21%7D%7D+%3D+%5Cepsilon+b+%2B+%5Cdfrac%7B%5Cleft%28%5Cepsilon+b%5Cright%29%5E%7B3%7D%7D%7B3%21%7D+%2B+%5Ccdots+%3D+%5Cepsilon+b+%5C+++%5C%5C+%5Ccos%5Cleft%28%5Cepsilon+b%5Cright%29+%26%3D+%5Csum_%7Bn%3D0%7D%5E%7B%5Cinfty%7D%7B%5Cleft%28-1%5Cright%29%5E%7Bn%7D%5Cdfrac%7B%5Cleft%28%5Cepsilon+b%5Cright%29%5E%7B2n%7D%7D%7B%5Cleft%282n%5Cright%29%21%7D%7D+%3D+1+%2B+%5Cdfrac%7B%5Cleft%28%5Cepsilon+b%5Cright%29%5E%7B2%7D%7D%7B2%7D+%2B+%5Ccdots+%3D+1.+%5Cend%7Balign%7D+)
得到
![[公式]](https://www.zhihu.com/equation?tex=%5Cbegin%7Balign%7D+++y+%26+%3D+%5Csin%5Cleft%28a%5Cright%29+%2B+%5Ccos%5Cleft%28a%5Cright%29+b+%5Cepsilon.+%5Cend%7Balign%7D+)
可以看到,二元部 ![[公式]](https://www.zhihu.com/equation?tex=%5Ccos%28a%29) 恰好就是原函数
恰好就是原函数 ![[公式]](https://www.zhihu.com/equation?tex=%5Csin%28a%29) 的导数。
的导数。
Reverse Mode
这个模式就比较简单和直接了。就是说,上面那个表里面,我每次只计算每个“小运算”的梯度(也是是那个图里面的每个节点),最后我再根据 chain rule 把“小运算”们的梯度串起来。其实 forward mode 和 reverse mode 并没有本质的区别,只是说,reverse mode在计算梯度先不考虑 chain rule,最后再用 chain rule 把梯度组起来。而前者则是直接就应用 chain rule 来算梯度。
下面总结一下 reverse mode 的流程:
- 创建计算图
- 计算前向传播的值及每个操作的梯度
- 这里没有
chain rule 的事
- 比如这个操作是乘法 $x_3 = x_1*x_2$,那么我们只需要把
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+x_3%7D%7B%5Cpartial+x_2%7D+%5C+%5C+%5C+%E4%BB%A5%E5%8F%8A+%5C+%5C+%5C+%5C+%5Cfrac%7B%5Cpartial+x_3%7D%7B%5Cpartial+x_1%7D) 算出来就好了
算出来就好了
- 反向计算梯度从最后一个节点(操作)开始:
![[公式]](https://www.zhihu.com/equation?tex=%5Coverline%7Bx%7D_%7BN%7D+%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x_%7BN%7D%7D+%3D+1+%5C+%5C+%5C+%2Cf%3Dx_N)
- 根据
chain rule 逐层推进 ![[公式]](https://www.zhihu.com/equation?tex=%5Coverline%7Bx%7D_%7BN-1%7D+%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x_%7BN%7D%7D%5Cdfrac%7B%5Cpartial+x_%7BN%7D%7D%7B%5Cpartial+x_%7BN-1%7D%7D)
- 假如有多条求导路径,我们要把他们加起来,例如
![[公式]](https://www.zhihu.com/equation?tex=%5Coverline%7Bx%7D%7B3%7D+%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7B3%7D%7D+%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x_%7B4%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B4%7D%7D%7B%5Cpartial+x_%7B3%7D%7D+%2B+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x_%7B5%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B5%7D%7D%7B%5Cpartial+x_%7B3%7D%7D+)
举个栗子,我们要计算函数
![[公式]](https://www.zhihu.com/equation?tex=+f%5Cleft%28x%2Cy%5Cright%29+%3D+xy+%2B+%5Cexp%5Cleft%28xy%5Cright%29+)
在点 ![[公式]](https://www.zhihu.com/equation?tex=a%3D%281%2C2%29) 的导数
的导数
首先还是先把计算图画出来
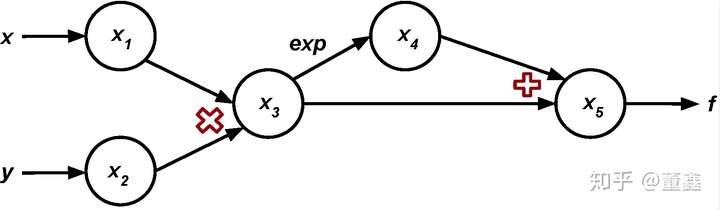
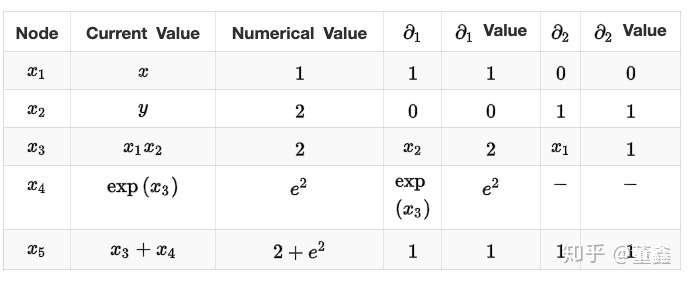
我们逐层的抽丝剥茧,
![[公式]](https://www.zhihu.com/equation?tex=+%5Cbegin%7Balign%7D+%5Coverline%7Bx%7D%7B5%7D+%26%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7B5%7D%7D+%3D+1%5C%5C++%5Coverline%7Bx%7D%7B4%7D+%26%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7B5%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B5%7D%7D%7B%5Cpartial+x_%7B4%7D%7D+%3D+1+%5Ccdot+1+%3D+1%5C%5C++%5Coverline%7Bx%7D%7B3%7D+%26%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7B4%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B4%7D%7D%7B%5Cpartial+x_%7B3%7D%7D+%2B+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x_%7B5%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B5%7D%7D%7B%5Cpartial+x_%7B3%7D%7D%3D+1+%5Ccdot+e%5E%7B2%7D+%2B+1%5Ccdot+1+%3D+1+%2B+e%5E%7B2%7D%5C%5C+%5Coverline%7Bx%7D%7B2%7D+%26%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7B3%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B3%7D%7D%7B%5Cpartial+x_%7B2%7D%7D+%3D+%5Cleft%281+%2B+e%5E%7B2%7D%5Cright%29x_%7B1%7D+%3D++1+%2B+e%5E%7B2%7D+%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+y%7D+%5C%5C+%5Coverline%7Bx%7D%7B1%7D+%26%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7B3%7D%7D%5Cdfrac%7B%5Cpartial+x_%7B3%7D%7D%7B%5Cpartial+x_%7B1%7D%7D+%3D++%5Cleft%281+%2B+e%5E%7B2%7D%5Cright%29x_%7B2%7D+%3D++2+%2B+2e%5E%7B2%7D+%3D+%5Cdfrac%7B%5Cpartial+f%7D%7B%5Cpartial+x%7D++%5Cend%7Balign%7D+)
总结
- 可以很清楚的看到,在训练人工神经网络时常用的
backpropagation 也是属于 reverse mode 的。
- 假如我们要计算的梯度的函数是
![[公式]](https://www.zhihu.com/equation?tex=f%3A%5Cmathbb%7BR%7D%5Em%5Crightarrow%5Cmathbb%7BR%7D%5En)
- 如果 n 是相对比较大的话,用
forward 比较省计算
- 如果 m 是相对比较大的话,用
reverse 比较省计算

,可以根据上面的图得到一个表格

,也要算 backward 的值
。
相当于多了一个 y 轴出来。
前面的系数,就是导数。举个栗子, 我们要求
,所以
恰好就是原函数
的导数。
算出来就好了
的导数





 浙公网安备 33010602011771号
浙公网安备 33010602011771号