神经网络与深度学习笔记 Chapter 3.
交叉熵
交叉熵是用于解决使用二次代价函数时当单个神经元接近饱和的时候对权重和bias权重学习的影响。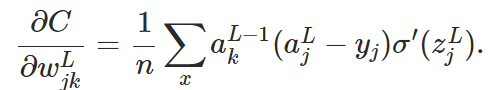 这个公式可以看出,当神经元饱和的时候,sigma的偏导接近于0,w的学习也会变小。但是应用交叉熵作为代价函数的话,只有当所有的神经元接近0或者1的时候才会出现这种情况。它解决了初始化w和bias时坏的w和bias带来的影响。
这个公式可以看出,当神经元饱和的时候,sigma的偏导接近于0,w的学习也会变小。但是应用交叉熵作为代价函数的话,只有当所有的神经元接近0或者1的时候才会出现这种情况。它解决了初始化w和bias时坏的w和bias带来的影响。
交叉熵对w求偏导:
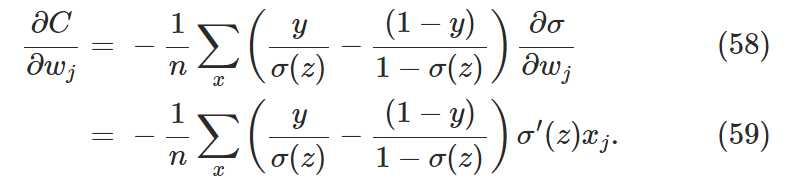
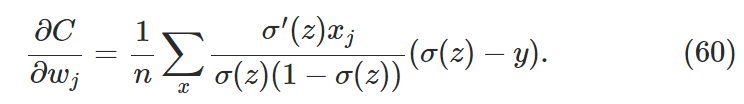 ,,,,有
,,,,有![]()
最后得出: 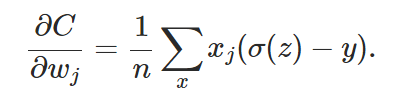 由该公式可以看出,只有大部分样例的输出接近期望值时,w的学习才会变缓。bias同理。
由该公式可以看出,只有大部分样例的输出接近期望值时,w的学习才会变缓。bias同理。
上面的讨论只针对有一个神经元的网络。
如果代价函数是交叉熵函数,那么对应的BP1为:![]() BP4为
BP4为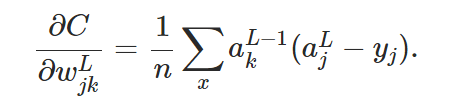 ,可以看出,该公式中消除了delta对z的偏导。
,可以看出,该公式中消除了delta对z的偏导。
但是,对于线性神经元且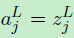 ,二次代价函数的误差为
,二次代价函数的误差为![]() ,从而有:
,从而有:
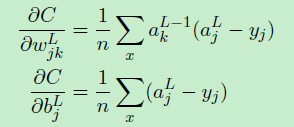
这说明当神经元是线性的时候,就不存在学习率下降的情况了。与此同时,这个时候神经元的误差可以称为是a与期望值的差。
Overfitting and regularization
过度拟合在神经网络中的表现是,当训练周期太长时,对测试集的准确率一直在摇摆,而训练集的损失(cost)在一直降低,这个时候就相当于网络在记住训练集中的特性,而不是进行更具一般性的学习。所以我们需要知道过拟合什么时候发生,学习降低过拟合的影响的技术。
一般来说减少过拟合的方法之一就是增加训练集的大小,但是有时候训练数据的获取并不是那么容易。
另一个减少过拟合的方法是正则化,本章将讲述正则化技术的一种权重衰减(weight decay)或L2正则化。该方法是添加一个正则项(regularization term)到损失函数中,添加正则项的损失函数如下所示:
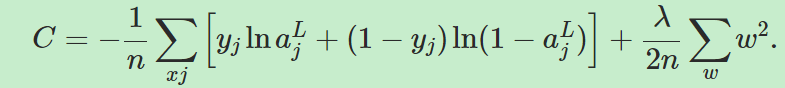 或
或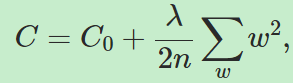
其中![]() 叫做正则化参数( regularization parameter),而n一般是训练集的大小,注意正则项中不包含bias。
叫做正则化参数( regularization parameter),而n一般是训练集的大小,注意正则项中不包含bias。





