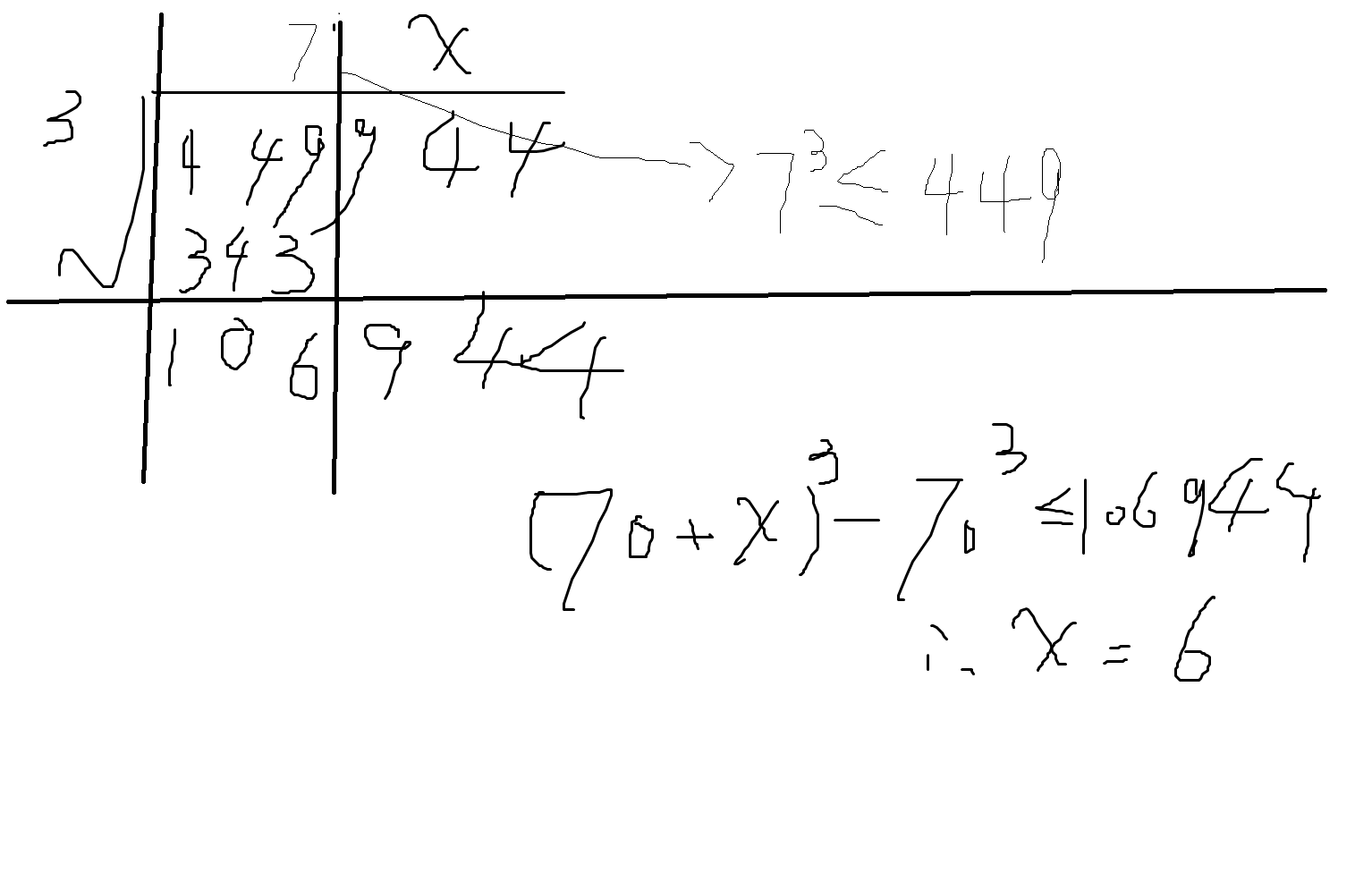手动开根号, 开三次根号

首先是牛顿法:
牛顿法:
https://blog.csdn.net/qq_36330643/article/details/78003952

这里:
\(y=f(x_0)+(x-x_0)f^{'}(x_0)\)
\(y=0, x=x_{k+1},x=x_k\)
\(x_{k+1}=x_{k}-f(x_k)/f^{'}(x_k)\)

计算 \(\sqrt{452}\)

\(f(x)=x^{2}-452\)
\(x_{k+1}=x_{k}-x_{k}/2+266/x_{k}\)
x0=20, x1=21.3 x2=21.26
但是第一个20给的必须比较接近,否则会不收敛.算不出来.

经过3次迭代就算出根号的数值了.

===========会发现上面也使用了大量的小数除法也很烦躁.

====下面是直接手动开根号用的就是初中的平方和公式.

方法可以看:https://www.bilibili.com/video/BV1Bu4y1H7kY/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=d68ed178f151e80fea1e02efd205802c
下面是我对于这个方法的细节分析, 让用户更好理解.
道理很简单. 只是注意每次计算都要带着小数点.因为小数点的差别巨大. 举哥栗子: 9的平方是81,往大数走, 0.9的平方是0.81, 数位往小了走.

还是算452的根号.
上来. 小数左边两两分开,小数右边两两分开.
也就是4|52|00|

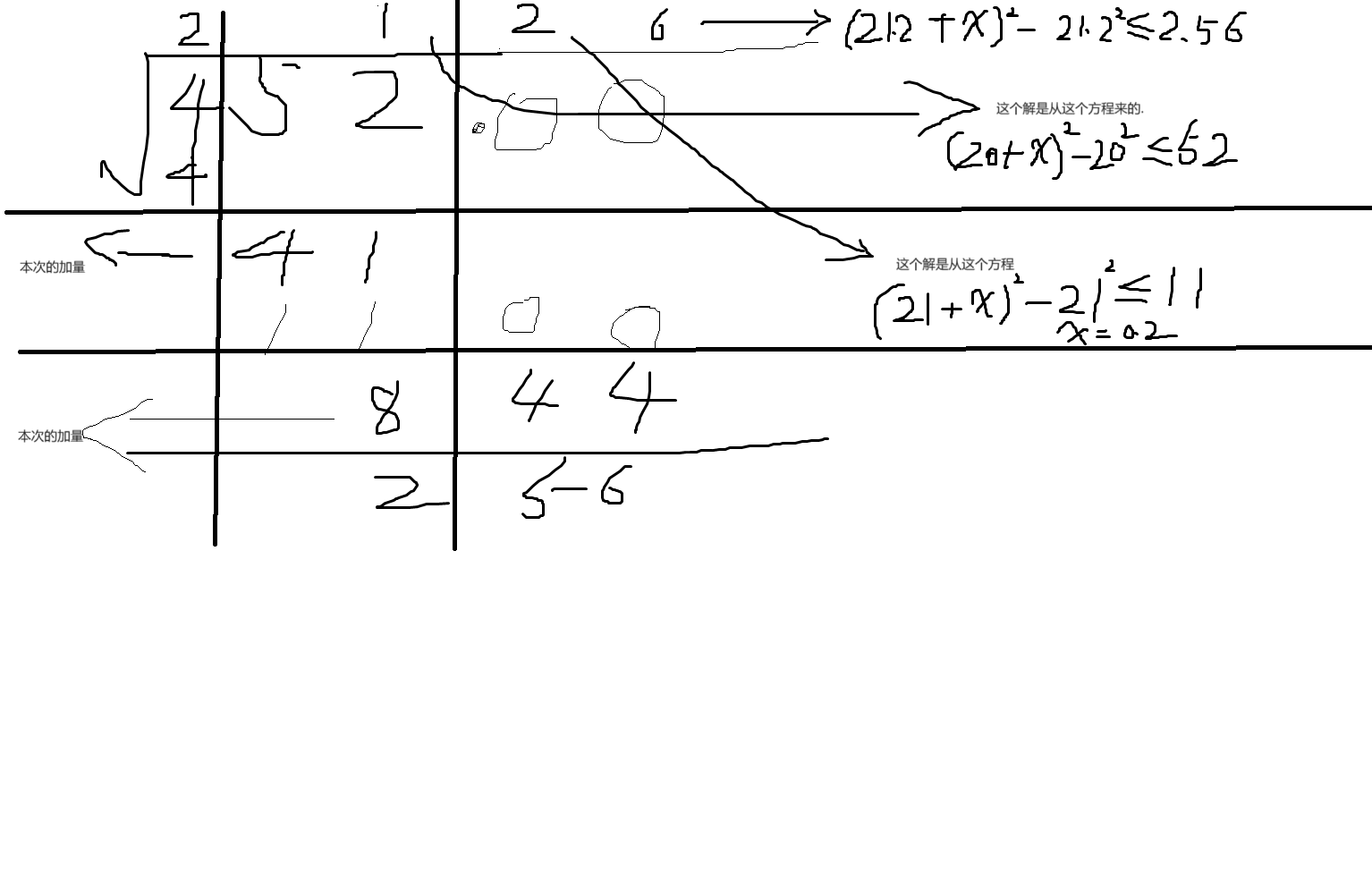
答案是21.26

举例子一个大整数开44944.

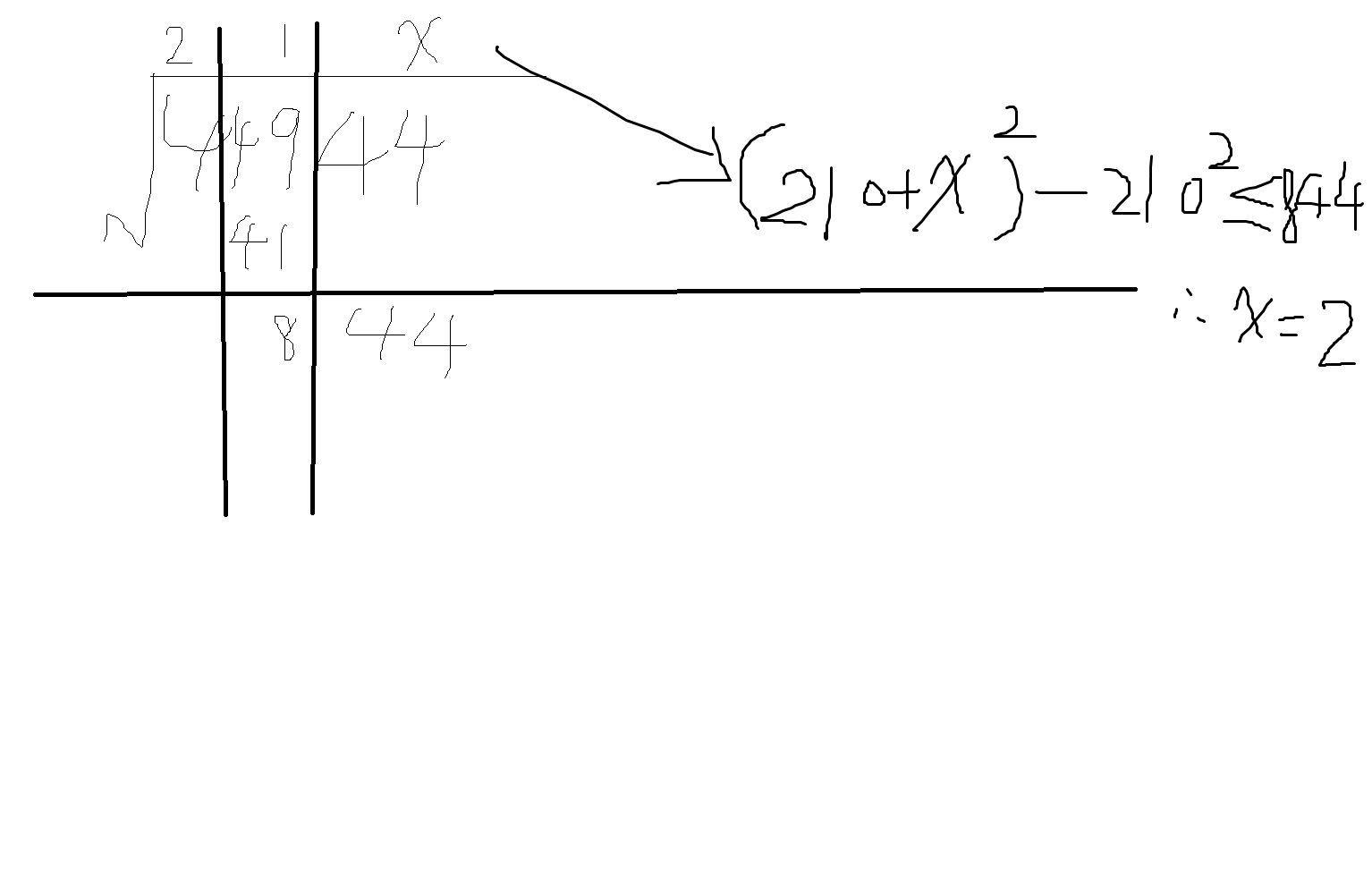
三次根号.
从右到左每3个分割.