xorshift 论文解析

论文地址
// xorshift paper: https://www.jstatsoft.org/article/view/v008i14/xorshift.pdf

1. 介绍.

方法: 把一个数跟他自己shift之后的数做异或. 重复几次得到的数就是一个随机数. 用c语言来说就是y^(y<<a) or y^(y>>a)

2.理论:

数学上RNG算法可以写作. 我们给一个种子集合Z, 他由m-对组成. \((x_1,....x_m)\), 还有一个单-单的函数f()定义在Z上. 也就是f输入一个数,输出一个数. 如果z是Z上随机抽取的数, 那么f(z)也是Z上随机生成的数.(从概率上)

对于xorshift这个RNG算法, Z表示全部的1\(\times\)n的二进制向量. \(\beta=(b1,...bn)\),n取32,64,96. bi取0或者1,所以每个元素都可以看做32-bit的计算机单词的组合.(因为每个n都是32的倍数), 我们定义变换矩阵为T.是一个\(n\times\)n的矩阵.

2.1 矩阵T生成全部的非0 二进制向量

定理: 让T生成全部的1\(\times\)n 二进制向量在\(\beta, \beta T,\beta T^2\) 等价于在n*n这个二进制矩阵群上, T的置是\(2^n-1\).
证明: 显然的. 因为置就是周期概念.

3. Xorshift应用

L是次对角矩阵全是1的矩阵
T=I+\(L^a\)
y^(y<<a)就是T矩阵的变换.
举个例子来说明这个等式:

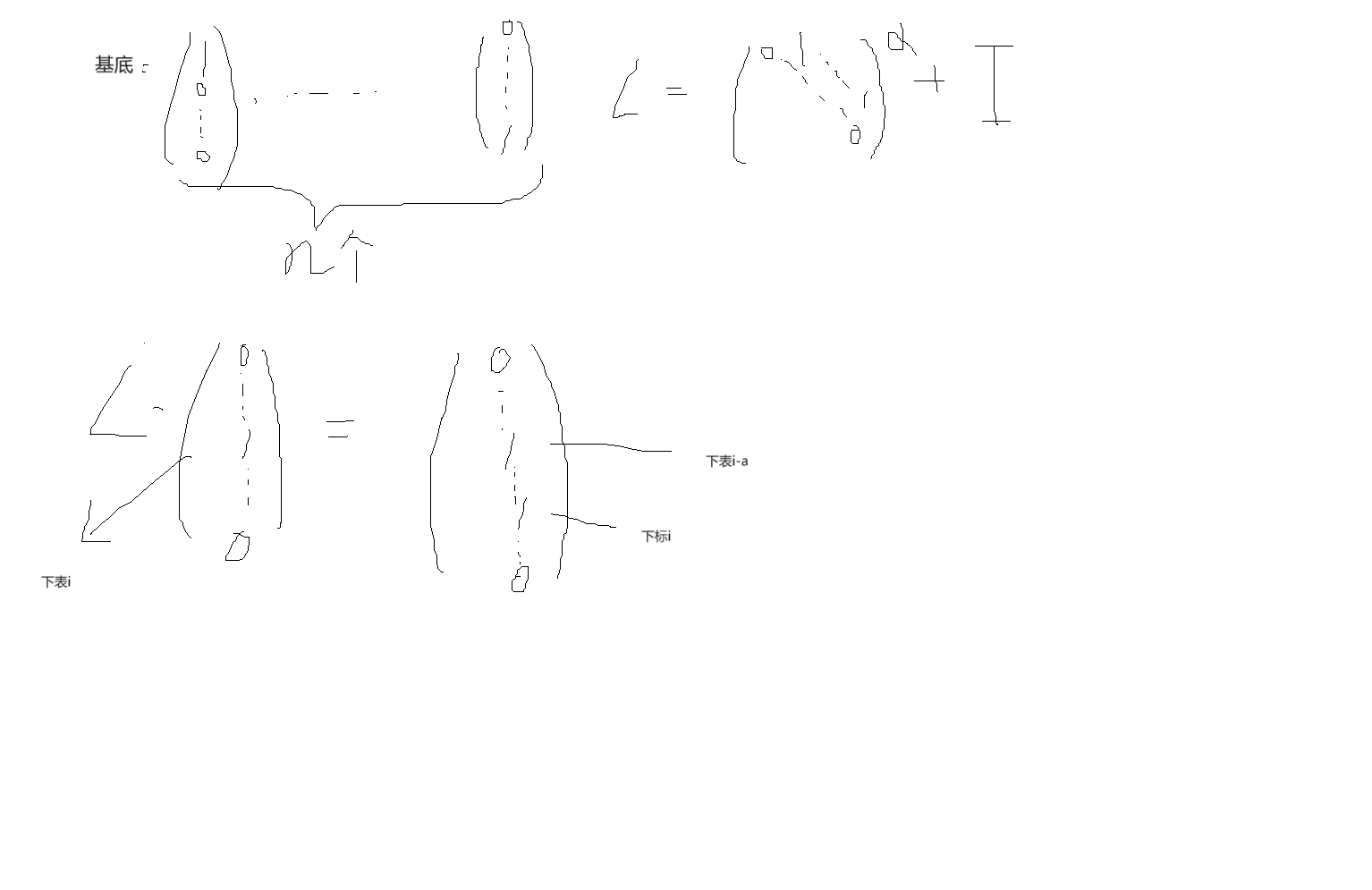
我们定义R=L的转置.
同理我们有\(I+R^b\)是y^(y>>b)的表示

我们注意到这个空间是mod2的.因为二进制.所以我们有
\(I+L^a+L^{2a}+L^{3a}+...\)是(\(I+L^a\))的逆变换.

首先我们考虑一次变换:
也就是T=I+\(L^a\), 显然n次之后必为I.所以周期不是\(2^n-1\).

我们考虑2次变化:
T=(I+\(L^a\))(I+\(L^b\)),对于n=32,64, 我们计算T周期是不是\(2^n-1\),我们只需要计算机暴力测试T做平方 n次.(每次都平方n次,所以得到T的2n次幂),我们检测他是不是T即可.这个是计算机测试,结果没有合适的a和b.
然而, 对于TT=(I+\(L^a\))(I+\(L^b\))(I+\(L^c\))我们也可以测试. 结果有81组解.详见论文.

3.1对于n=96,128,160...

下面就是一些矩阵分解.有兴趣可以拓展一下.