插头dp学习总结
定义
一类特殊的状态压缩dp,又称轮廓线dp
作用
通常用于解决二维空间的状态压缩问题,且每个位置的取值只与临近的几个位置有关,适用于超小数据范围,网格图,连通性等问题。
模板
#include<bits/stdc++.h>
#define md 312251
#define mxn 15
using namespace std;
int mp[mxn][mxn],hs[md+2],k,n,m,nn,mm;
unsigned long long f[2][600000];long long ans,g[2][600000];
char ch[mxn];
int tot[2],mi[mxn];//f:state g:sum
void prework(){
for(int i=1;i<=max(n,m);i++)
mi[i]=i<<1;
}
void put(unsigned long long cur,long long val){
int s=cur%md;
while(hs[s]){
if(f[k][hs[s]]==cur){
g[k][hs[s]]+=val;
return;
}
s++;if(s==md) s=0;
}
hs[s]=++tot[k];f[k][hs[s]]=cur;g[k][hs[s]]=val;
}
void solve(){
tot[0]=1;g[0][1]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
k^=1;tot[k]=0;
memset(hs,0,sizeof(hs));
memset(f[k],0,sizeof(f[k]));
memset(g[k],0,sizeof(g[k]));
for(int u=1;u<=tot[k^1];u++){
unsigned long long state=f[k^1][u];
long long val=g[k^1][u];
int p=(state>>mi[j-1])%4,q=(state>>mi[j])%4;
if(!mp[i][j]){
if(!p&&!q) put(state,val);
}else{
if(!p){
if(!q){
if(mp[i+1][j]&&mp[i][j+1])
put(state+1*(1<<mi[j-1])+2*(1<<mi[j]),val);
}
if(q==1){
if(mp[i][j+1]) put(state,val);
if(mp[i+1][j]) put(state-q*(1<<mi[j])+q*(1<<mi[j-1]),val);
}
if(q==2){
if(mp[i][j+1]) put(state,val);
if(mp[i+1][j]) put(state-q*(1<<mi[j])+q*(1<<mi[j-1]),val);
}
}
if(p==1){
if(!q){
if(mp[i+1][j]) put(state,val);
if(mp[i][j+1]) put(state-p*(1<<mi[j-1])+p*(1<<mi[j]),val);
}
if(q==1){
int cur=1,s;
for(int v=j+1;v<=m;v++){
s=(state>>mi[v])%4;
if(s==1) cur++;
if(s==2) cur--;
if(!cur){
s=state-p*(1<<mi[j-1])-q*(1<<mi[j])-(1<<mi[v]);
break;
}
}
put(s,val);
}
if(q==2){
if(i==nn&&j==mm) ans+=val;
}
}
if(p==2){
if(!q){
if(mp[i+1][j]) put(state,val);
if(mp[i][j+1]) put(state-p*(1<<mi[j-1])+p*(1<<mi[j]),val);
}
if(q==1){
put(state-p*(1<<mi[j-1])-q*(1<<mi[j]),val);
}
if(q==2){
int cur=1,s;
for(int v=j-2;v>=1;v--){
s=(state>>mi[v])%4;
if(s==2) cur++;
if(s==1) cur--;
if(!cur){
s=state-p*(1<<mi[j-1])-q*(1<<mi[j])+(1<<mi[v]);
break;
}
}
put(s,val);
}
}
}
}
}
for (int j=1;j<=tot[k];j++)
f[k][j]=f[k][j]<<2;
}
}
void work(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%s",ch);
for(int j=0;j<m;j++)
if(ch[j]=='.') mp[i][j+1]=1,nn=i,mm=j+1;
}
prework();
solve();
printf("%lld\n",ans);
}
int main(){
work();
return 0;
}
例题
HDU1565 方格取数(1)
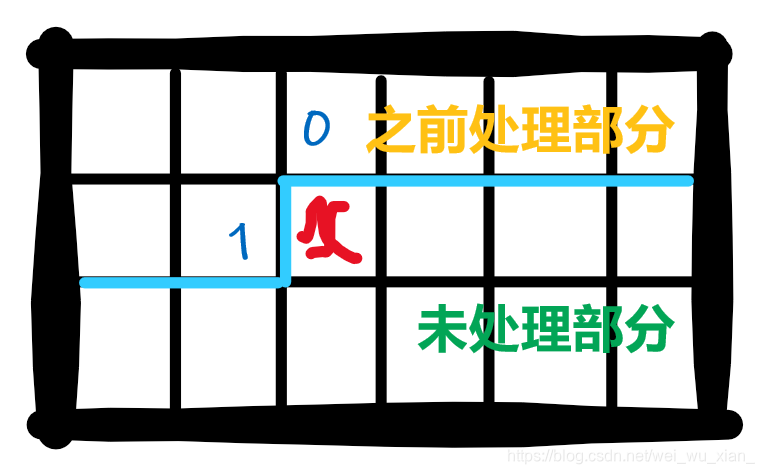
思路:基础模板题,放一张图就知道了:
C
o
d
e
Code
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=21;
int dp[2][1<<N],n,v;
void solve(){
memset(dp,0,sizeof(dp));
int pre=0,now=1;
dp[pre][0]=0;
int ans=0;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
scanf("%d",&v);
for(int S=0;S<(1<<n);S++){//轮廓线状态
int newS=S&(~(1<<j));
dp[now][newS]=max(dp[now][newS],dp[pre][S]);
if((S&(1<<j))==0&&(j==0||(S&(1<<(j-1)))==0))//上面和左均为0,可以取数
dp[now][S|(1<<j)]=max(dp[now][S|(1<<j)],dp[pre][S]+v);
}
swap(pre,now);
}
}
for(int S=0;S<(1<<n);S++)
ans=max(ans,dp[pre][S]);
printf("%d\n",ans);
}
int main(){
while(~scanf("%d",&n)){
solve();
}
return 0;
}
原题: HDU-1693 Eat the Trees
题目翻译:
我们大多数人都知道,在名为DotA(古代防御)的游戏中, 帕吉在游戏的第一阶段是一个强大的英雄。但是,当游戏结束时,帕吉不再是一个强大的英雄。 因此,帕吉(Pudge)的队友为他分配了新任务-吃树! 这些树的大小为N * M个矩形,每个单元要么只有一棵树,要么根本没有。帕吉要做的就是吃掉牢房里的所有树木。 Pudge必须遵循以下几条规则: I.帕吉必须选择回路来吃掉树木,然后他才能吃掉所选回路中的所有树木。 二。不包含树的单元格无法访问,例如通过Pudge选择的通过回路的每个单元必须包含一棵树,并且当选择回路时,回路中单元中的树将消失。 三,帕吉人可以选择一个或多个回路来吃树。 现在帕吉有一个问题,那里有几种吃树的方法? 在下面的图片中,给出了N = 6和M = 3的三个样本(灰色正方形表示单元中没有树,黑色粗线表示所选的电路)
思路:

C
o
d
e
Code
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
long long dp[2][1<<12];
long long ans;
int n,m,v;
void solve(){
int total=1<<(m+1);
int pre=0,now=1;
memset(dp[pre],0,sizeof(dp[pre]));
dp[pre][0]=1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
scanf("%d",&v);
memset(dp[now],0,sizeof(dp[now]));
int j0=1<<j;
int j1=j0<<1;
for(int S=0;S<total;S++){
bool p=S&j0,q=S&j1;//前一个格子的左,上状态
if(v==0){//障碍物,不可行
if(!p&&!q)
dp[now][S]+=dp[pre][S];
}else{
if(p^q)//有一个为1,一个为0
dp[now][S]+=dp[pre][S];//原状态不变
dp[now][S^j0^j1]+=dp[pre][S];//相反状态
}
}
swap(pre,now);//处理完一个格子后交换
}
memset(dp[now],0,sizeof(dp[now]));//为处理下一行做准备
for(int S=0;S<total/2;S++)//最后的状态最大0111...1
dp[now][S<<1]=dp[pre][S];//也可以+=,速度更快15ms,=,46ms
swap(pre,now);//交换后的pre是处理过的结果,为下一行做准备
}
ans=dp[now][0];
}
int main(){
int T,cas=1;
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m);
solve();
printf("Case %d: There are %I64d ways to eat the trees.\n",cas++,ans);
}
return 0;
}
原题:POJ-1739 Tony’s Tour
题目翻译:
一个正方形城镇已被划分为n * m(n行和m列)平方图(1 <= N,M <= 8),其中一些被阻塞,其他未被阻塞。农场位于左下图,市场位于右下图。托尼(Tony)沿着每一个畅通无阻的地块走了一次,从农场到集市进行了整个小镇之旅。 编写一个程序,计算Betsy从农场到市场可以带多少次独特的旅行。
思路:

C
o
d
e
Code
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
LL dp[2][1<<20];//记录方案数
int state[2][1<<20];//记录状态,S=state[pre][s],pre为前一个格子标记,s为状态编号,S为状态
int total[2];//记录状态总数
int pre,now;
int endx,endy;//记录最后一个非障碍格子
bool map[15][15];
char str[200];
int m,n;
LL ans;
const int HASH=4001;//坑点!!哈希值太大会超时!本题m<=10,用4位数素数,如3007,5位素数时间更多
int Hash[HASH];//记录S对应的哈希值x的状态编号
void HashIn(int S,LL num){
int x=S%HASH;
while(~Hash[x]&&state[now][Hash[x]]!=S){//线性探测
x++;
x%=HASH;
}
if(Hash[x]==-1){//未找到,加入hash表中
dp[now][total[now]]=num;
state[now][total[now]]=S;
Hash[x]=total[now];//记录状态编号
total[now]++;
}
else//找到,累加方案数
dp[now][Hash[x]]+=num;
}
void init(){
memset(map,0,sizeof(map));
endx=-1;
for(int i=0;i<n;i++){
scanf("%s",str);
for(int j=0;j<m;j++){
if(str[j]=='.'){
map[i][j]=1;
endx=i;
endy=j;
}
else
map[i][j]=0;
}
}
if(map[n-1][0]==0||map[n-1][m-1]==0)//最后一行的左角或右角不可达
endx=endy=-1;
else{
endx=n+1;
endy=m-1;
}
for(int j=0;j<m;j++){//增加两行,第一行首尾可行,其它不可行,第二行均可行
map[n][j]=0;
map[n+1][j]=1;
}
map[n][0]=map[n][m-1]=1;
n+=2;//注意 这里将矩形扩大 方便后面的使用
}
//位运算,取S按长度l的第p位
int getV(int S,int p,int l=2){//4进制,l=2;8进制,l=3
return (S>>(p*l))&((1<<l)-1);
}
//位运算,设置S按长度l的第p位值为v
void setV(int& S,int p,int v,int l=2){
S^=getV(S,p)<<(p*l);//第p位置0
S|=v<<(p*l);//第p位置v
}
void memsetnow(){//哈希每次用后清空
memset(Hash,-1,sizeof(Hash));
total[now]=0;
}
void solve(){
init();
if(endx==-1){
puts("0");
return;
}
pre=0,now=1;
ans=0;
memsetnow();
dp[pre][0]=1;
state[pre][0]=0;
total[pre]=1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
memsetnow();
for(int s=0;s<total[pre];s++){//s为状态编号
if(dp[pre][s])
{
LL num=dp[pre][s];
int S=state[pre][s];
int p=getV(S,j);
int q=getV(S,j+1);
if(map[i][j]==0){//有障碍
if(p==0&&q==0)
HashIn(S,num);
continue;
}
if(p==0&&q==0){//p、q均为0,第一种情况
if(map[i+1][j]&&map[i][j+1]){
int nS=S;
setV(nS,j,1);
setV(nS,j+1,2);
HashIn(nS,num);
}
continue;
}
if((p>0)^(q>0)){//p、q有一个为0,第二种情况
if(map[i+(p>0)][j+(q>0)])
HashIn(S,num);
if(map[i+(q>0)][j+(p>0)]){
int nS=S;
setV(nS,j,q);//p、q交换
setV(nS,j+1,p);
HashIn(nS,num);
}
continue;
}
if(p==1&&q==1){//第三种情况,3.1
int find=1;
for(int v=j+2;v<=m;v++){//向后搜q匹配的右括号),改为左括号
int k=getV(S,v);
if(k==1)
find++;
else if(k==2)
find--;
if(find==0){
int nS=S;
setV(nS,j,0);//p、q置0
setV(nS,j+1,0);
setV(nS,v,1);//改为左括号
HashIn(nS,num);
break;
}
}
continue;
}
if(p==2&&q==2){//第三种情况,3.2
int find=1;
for(int v=j-1;v>=0;v--){//向前搜p匹配的左括号(,改为右括号
int k=getV(S,v);
if(k==2)
find++;
else if(k==1)
find--;
if(find==0){
int nS=S;
setV(nS,j,0);//p、q置0
setV(nS,j+1,0);
setV(nS,v,2);//改为右括号
HashIn(nS,num);
break;
}
}
continue;
}
if(p==2&&q==1){//第三种情况,3.3
int nS=S;
setV(nS,j,0);//p、q置0
setV(nS,j+1,0);
HashIn(nS,num);
continue;
}
if(p==1&&q==2){//第三种情况,3.4
if(i==endx&&j==endy)//最后一个非障碍格子
ans+=num;
}
}
}
swap(now,pre);
}
memsetnow();
for(int s=0;s<total[pre];s++)
if(dp[pre][s]){
LL num=dp[pre][s];
int S=state[pre][s]<<2;//左移一格
HashIn(S,num);
}
swap(now,pre);
}
printf("%I64d\n",ans);
}
int main(){
while(~scanf("%d%d",&n,&m),n+m){
if(n==1&&m==1){//只有一格特殊处理
scanf("%s",str);
if(str[0]=='.') printf("1\n");
else printf("0\n");
continue;
}else if(m==1){//只有一列多行的情况
int ok=1;
for(int i=0;i<n;i++){
scanf("%s",str);
if(str[0]=='.'&&i<n-1)
ok=0;
}
if(str[0]=='#')
ok=0;
printf("%d\n",ok);
continue;
}
solve();
}
return 0;
}
原题:URAL-1519 Formula 1
题目翻译:
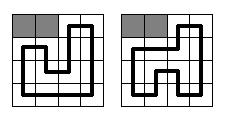
谁会足够聪明地制定电路规划并让城市免受不可避免的耻辱?当然,只有真正的专业人员-本地技术大学一线团队中经过战斗的程序员!..但是我们的英雄们并没有在寻找轻松的生活,而是提出了更加困难的问题:“当然,如果我们找到了,我们的市长会很高兴的。有多少种构建电路的方法!” - 他们说。 应该说,沃洛格达州的赛道将非常简单。这将是一个大小为N * M的矩形单元,每个单元都构建一个单个电路段。每个线段应平行于矩形的一侧,因此电路上只能有直角的弯曲。在下面的图片中,给出了两个样本,其中N = M = 4(灰色正方形表示地鼠孔,粗黑线表示竞赛电路)。这里没有其他方法可以构建电路。
思路:

C
o
d
e
Code
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
LL dp[2][1<<24];//记录方案数
int state[2][1<<24];//记录状态,S=state[pre][s],pre为前一个格子标记,s为状态编号,S为状态
int total[2];//记录状态总数
int pre,now;
int endx,endy;//记录最后一个非障碍格子
bool map[15][15];
int m,n;
LL ans;
const int HASH=40001;//坑点!!哈希值太小会超时!4位素数超时,m<=12,用5位数素数,如30007
int Hash[HASH];//记录S对应的哈希值x的状态编号
void HashIn(int S,LL num){
int x=S%HASH;
while(~Hash[x]&&state[now][Hash[x]]!=S){//线性探测
x++;
x%=HASH;
}
if(Hash[x]==-1){//未找到,加入hash表中
dp[now][total[now]]=num;
state[now][total[now]]=S;
Hash[x]=total[now];//记录状态编号
total[now]++;
}
else//找到,累加方案数
dp[now][Hash[x]]+=num;
}
void init(){
memset(map,0,sizeof(map));
endx=-1;
for(int i=0;i<n;i++){
char str[200];
scanf("%s",str);
for(int j=0;j<m;j++){
if(str[j]=='*')
map[i][j]=0;
else if(str[j]=='.'){
map[i][j]=1;
endx=i;
endy=j;
}
}
}
}
//位运算,取S按长度l的第p位
int getV(int S,int p,int l=2){//4进制,l=2;8进制,l=3
return (S>>(p*l))&((1<<l)-1);
}
//位运算,设置S按长度l的第p位值为v
void setV(int& S,int p,int v,int l=2){
S^=getV(S,p)<<(p*l);//第p位置0
S|=v<<(p*l);//第p位置v
}
void memsetnow(){//哈希表清空
memset(Hash,-1,sizeof(Hash));
total[now]=0;
}
void solve()
{
init();
if(endx==-1){
puts("0");
return;
}
pre=0,now=1;
ans=0;
memsetnow();//哈希表清空
dp[pre][0]=1;
state[pre][0]=0;
total[pre]=1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
memsetnow();//哈希表清空
for(int s=0;s<total[pre];s++){
if(dp[pre][s]){
LL num=dp[pre][s];
int S=state[pre][s];
int p=getV(S,j);
int q=getV(S,j+1);
if(map[i][j]==0){//有障碍,第一种情况
if(p==0&&q==0)
HashIn(S,num);
continue;
}
if(p==0&&q==0){//p、q均为0,第二种情况
if(map[i+1][j]&&map[i][j+1]){
int nS=S;
setV(nS,j,1);
setV(nS,j+1,2);
HashIn(nS,num);
}
continue;
}
if((p>0)^(q>0)){//p、q有一个为0,第三种情况
if(map[i+(p>0)][j+(q>0)])
HashIn(S,num);
if(map[i+(q>0)][j+(p>0)]){
int nS=S;
setV(nS,j,q);//p、q交换
setV(nS,j+1,p);
HashIn(nS,num);
}
continue;
}
if(p==1&&q==1){//第四种情况,4.1
int find=1;
for(int v=j+2;v<=m;v++){//向后搜q匹配的右括号),改为左括号
int k=getV(S,v);
if(k==1)
find++;
else if(k==2)
find--;
if(find==0){
int nS=S;
setV(nS,j,0);//p、q置0
setV(nS,j+1,0);
setV(nS,v,1);//改为左括号
HashIn(nS,num);
break;
}
}
continue;
}
if(p==2&&q==2){//第四种情况,4.2
int find=1;
for(int v=j-1;v>=0;v--){//向前搜p匹配的左括号(,改为右括号
int k=getV(S,v);
if(k==2)
find++;
else if(k==1)
find--;
if(find==0){
int nS=S;
setV(nS,j,0);//p、q置0
setV(nS,j+1,0);
setV(nS,v,2);//改为右括号
HashIn(nS,num);
break;
}
}
continue;
}
if(p==2&&q==1){//第四种情况,4.3
int nS=S;
setV(nS,j,0);//p、q置0
setV(nS,j+1,0);
HashIn(nS,num);
continue;
}
if(p==1&&q==2){//第四种情况,4.4
if(i==endx&&j==endy)//最后一个非障碍格子
ans+=num;
}
}
}
swap(now,pre);
}
memsetnow();//哈希表清空
for(int s=0;s<total[pre];s++)
if(dp[pre][s]){
LL num=dp[pre][s];
int S=state[pre][s]<<2;//左移一格,四进制,一格用两位表示
HashIn(S,num);
}
swap(now,pre);
}
printf("%I64d\n",ans);
}
int main(){
while(~scanf("%d%d",&n,&m)){
solve();
}
return 0;
}

