哈夫曼树(Huffman Tree)学习总结
定义
将所要编码的字符作为叶子结点的树为哈夫曼树
作用
解决编码问题
模板
priority_queue<int,vector<int>,greater<int> >Q;
int total;
int n,x;
int main(){
cin>>n;
while(n--){
cin>>x;
Q.push(x);
}
while(Q.size()!=1){
int sum=0;
sum+=Q.top();
Q.pop();
sum+=Q.top();
Q.pop();
Q.push(sum);
total+=sum;
}
cout<<total;
return 0;
}
例题
P1090 合并果子 / [USACO06NOV] Fence Repair G
由题意可得,这是一道贪心题也是一道模板题。
解法1:
策略:合并消耗体力尽可能小的果子堆
思路:对每一堆果子进行排序,去最小的和第二小的两堆,求和后与ans相加,并将最小的和第二小的两堆之和插入回原数组,再次排序,以此类推。直到数组中仅剩下一个数,输出ans
优点:时间复杂度低,解决问题多(见P6033 合并果子 加强版)
缺点:代码较繁琐,可观性较弱
C o d e 1 : Code1: Code1:时间复杂度 O ( n ) O(n) O(n)
#include<bits/stdc++.h>
using namespace std;
int k=1,x,n,n1,n2,a[30001],b[30001],t[20001],w,ans;
int i=1,j=1;
int main(){
scanf("%d",&n);
memset(a,127/3,sizeof(a));
memset(b,127/3,sizeof(b));
for(int i=1;i<=n;i++){
scanf("%d",&x);
t[x]++;//初始化桶
}
for(int i=1;i<=20000;i++){//桶排序
while(t[i]!=0){
t[i]--;
a[++n1]=i;
}
}
while(k<n){
if(a[i]<b[j]){//取第一小的
w=a[i++];
}else{
w=b[j++];
}
if(a[i]<b[j]){//取第二小的
w+=a[i++];
}else{
w+=b[j++];
}
b[++n2]=w;//加入第二个队列
k++;//计算合并次数
ans+=w;//计算价值
}
printf("%d",ans);
return 0;
}
解法2:
策略:合并消耗体力尽可能小的果子堆
思路:将每一堆果子用堆维护(不懂堆的见基本数据结构――堆的基本概念及其操作 JVxie编),取出堆顶元素(第一小的),弹出堆顶元素;再取出一次堆顶元素(第二小的),求和,再弹出,最后将和插入堆内,再将ans与第一小和第二小元素之和相加,以此类推,直到堆中仅剩1个元素,输出ans
优点:代码较简洁,可观性较强
缺点:时间复杂度较高,解决问题较少(见P6033 合并果子 加强版)
思路图解:
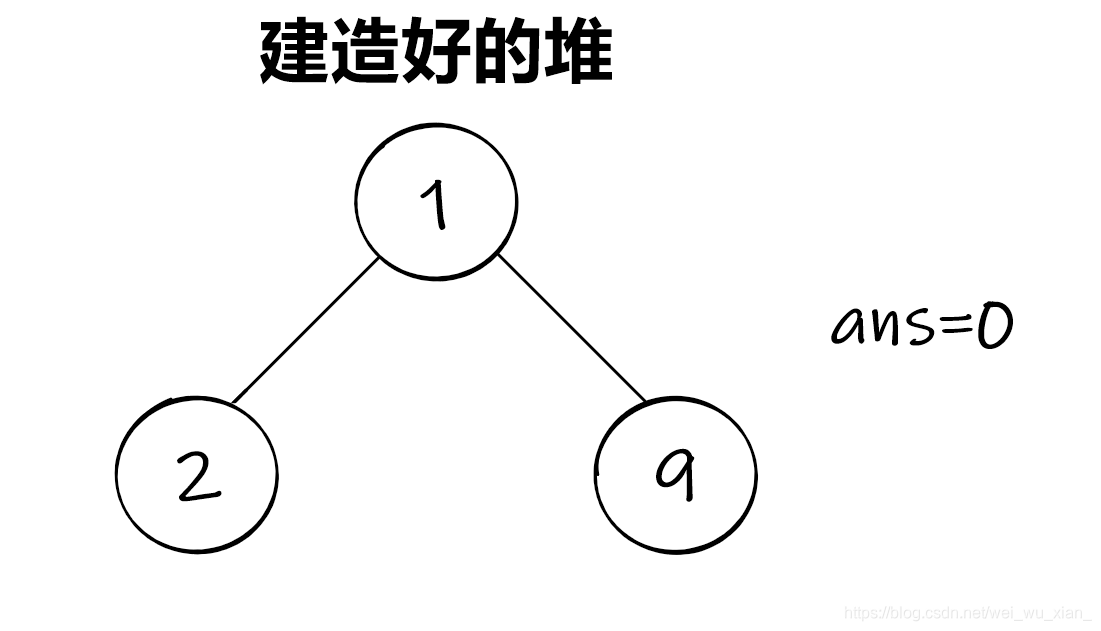
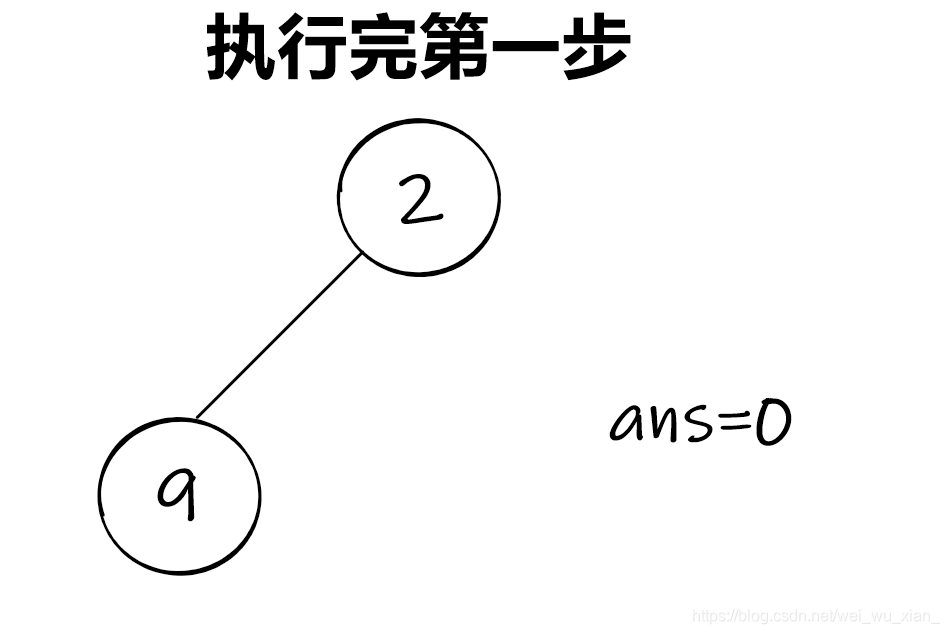
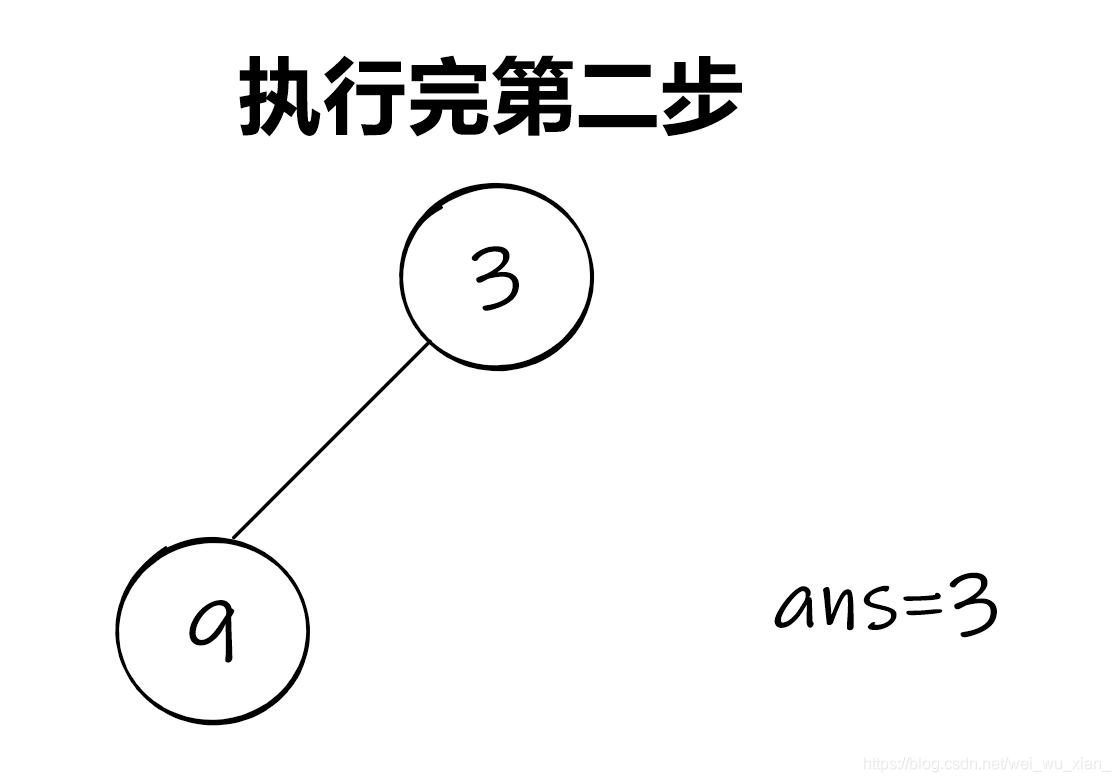
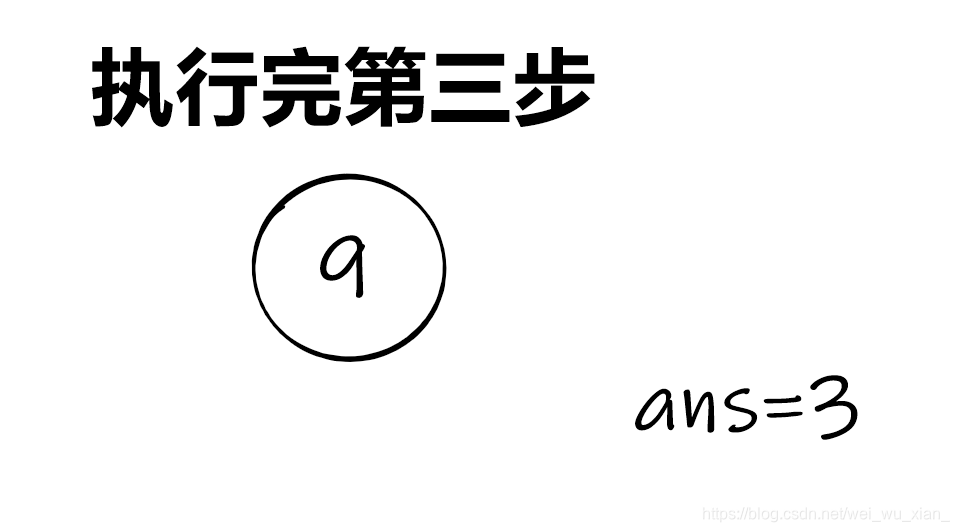
C o d e 2 : Code2: Code2:时间复杂度: O ( n l o g n ) O(nlogn ) O(nlogn)
#include<bits/stdc++.h>
using namespace std;
int n,x;
priority_queue<int,vector<int>,greater<int> >q;//定义堆
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>x;
q.push(x);//每一堆果子用堆维护
}
int ans=0;
while(q.size()>=2){
int a=q.top(); q.pop();//取出第一小的堆顶元素,弹出堆顶元素
int b=q.top(); q.pop();//取出第二小的堆顶元素,弹出堆顶元素
ans+=a+b;//将ans与第一小和第二小元素之和相加
q.push(a+b);//求和,并将和插入堆内
}
cout<<ans;
return 0;
}
她透过我的血,看到了另一抹殷红


