蒟蒻写的最小生成树学习总结

定义

在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得 w(T) 最小，则此 T 为 G 的最小生成树。

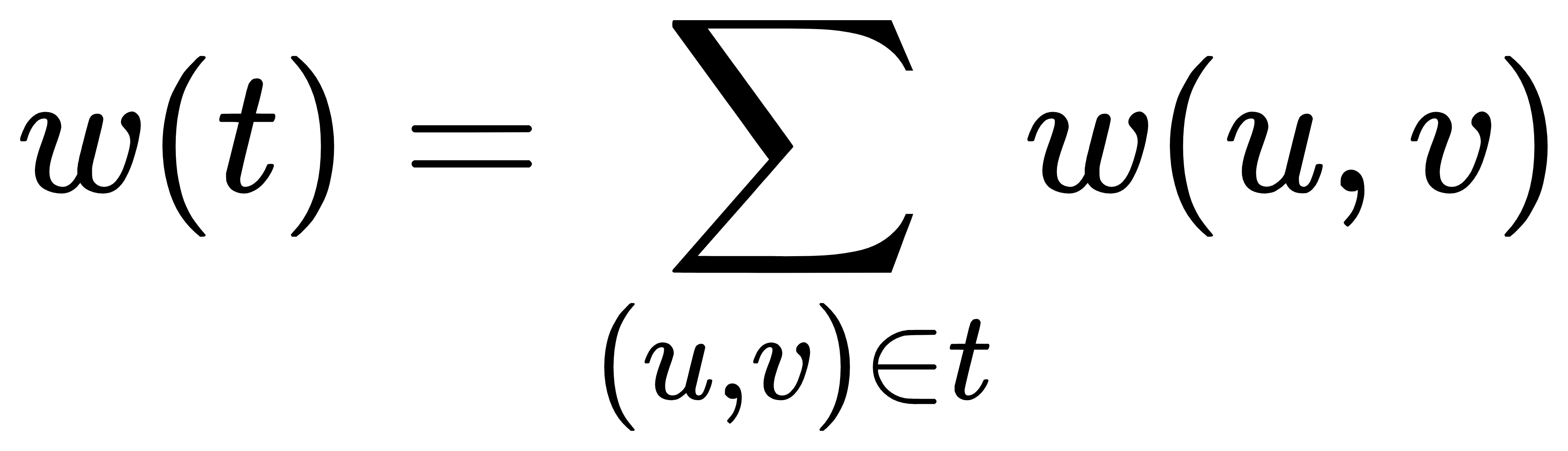
最小生成树其实是最小权重生成树的简称。

解决问题

要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

模板

Prim算法（选自Prim算法 虚心使人进步编）

#include<iostream>  
#include<fstream>  
using  namespace std;  
  
#define MAX 100  
#define MAXCOST 0x7fffffff  
  
int graph[MAX][MAX];  
  
int prim(int graph[][MAX], int n)  
{  
    int lowcost[MAX];  
    int mst[MAX];                                 
    int i, j, min, minid, sum = 0;  
    for (i = 2; i <= n; i++)  
    {  
        lowcost[i] = graph[1][i];  
        mst[i] = 1;                                       //mst[]存放MST外的点i到MST最短距离时候对应的MST里的点标号
    }  
    mst[1] = 0;  
    for (i = 2; i <= n; i++)                        //要找出n-1个点为止
    {  
        min = MAXCOST;  
        minid = 0;  
        for (j = 2; j <= n; j++)  
        {  
            if (lowcost[j] < min && lowcost[j] != 0)  
            {  
                min = lowcost[j];  
                minid = j;  
            }  
        }  
        cout << "V" << mst[minid] << "-V" << minid << "=" << min << endl;  
        sum += min;  
        lowcost[minid] = 0;  
        for (j = 2; j <= n; j++)  
        {  
            if (graph[minid][j] < lowcost[j])                //不更新的话，lowcost[j]存的只是上一时刻的Lowcost[j]，MST外部的点到minid的距离会不会比到之前的MST里点得最小距离小？
       {  
                lowcost[j] = graph[minid][j];  
                mst[j] = minid;                               //点j到MST内的lowcot对应的MST里的点事minid
            }  
        }  
    }  
    return sum;  
}  
  
int main()  
{  
    int i, j, k, m, n;  
    int x, y, cost;  
    ifstream in("input.txt");  
    in >> m >> n;//m=顶点的个数，n=边的个数  
    //初始化图G  
    for (i = 1; i <= m; i++)  
    {  
        for (j = 1; j <= m; j++)  
        {  
            graph[i][j] = MAXCOST;  
        }  
    }  
    //构建图G  
    for (k = 1; k <= n; k++)  
    {  
        in >> i >> j >> cost;  
        graph[i][j] = cost;  
        graph[j][i] = cost;  
    }  
    //求解最小生成树  
    cost = prim(graph, m);  
    //输出最小权值和  
    cout << "最小权值和=" << cost << endl;  
    system("pause");  
    return 0;  
}  

Kruskal算法（选自最小生成树（kruskal算法Superb_Day编）

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,tot=0,k=0;//n端点总数，m边数，tot记录最终答案，k已经连接了多少边 
int fat[200010];//记录集体老大 
struct node
{
	int from,to,dis;//结构体储存边 
}edge[200010];
bool cmp(const node &a,const node &b)//sort排序（当然你也可以快排） 
{
	return a.dis<b.dis;
}
int father(int x)//找集体老大，并查集的一部分 
{
	if(fat[x]!=x)
	return father(fat[x]);
	else return x;
}
void unionn(int x,int y)//加入团体，并查集的一部分 
{
	fat[father(y)]=father(x);
}
int main()
{
	scanf("%d%d",&n,&m);//输入点数，边数 
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&edge[i].from,&edge[i].to,&edge[i].dis);//输入边的信息 
	}
	for(int i=1;i<=n;i++) fat[i]=i;//自己最开始就是自己的老大 （初始化） 
	sort(edge+1,edge+1+m,cmp);//按权值排序（kruskal的体现） 
	for(int i=1;i<=m;i++)//从小到大遍历 
	{
		if(k==n-1) break;//n个点需要n-1条边连接 
		if(father(edge[i].from)!=father(edge[i].to))//假如不在一个团体 
		{
			unionn(edge[i].from,edge[i].to);//加入 
			tot+=edge[i].dis;//记录边权 
			k++;//已连接边数+1 
		}
	}
	printf("%d",tot);
	return 0;
}

例题

P2872 [USACO07DEC]Building Roads S

由题意可得，这是一道最小生成树题也是一道模板题

算法：Kruskal算法（时间复杂度较低）(动过手脚了，仔细哦，摘自P2872 [USACO07DEC]Building Roads S题解)

#include <iosteam>
using namespace std;
const int N = 5000100;
int n, m, cnt, fa[N], sum;
double ans;
struct Node {
	int x, y;
}E[N];
struct node {
	int from, to;
	double w;
}e[N];
int read() {
	int s = 0, w = 1;
	char ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') w = -1;ch = getchar();}
	while(isdigit(ch)) {s = s * 10 + ch - '0';ch = getchar();}
	return s * w;
}
void add(int x, int y, double z) {
	e[++cnt].from =x;
	e[cnt].to = y;
	e[cnt].w = z;
}
double jl(int x, int y) {
	return (double)(sqrt((double)(E[x].x - E[y].x) * (E[x].x - E[y].x) + (double)(E[x].y - E[y].y) * (E[x].y - E[y].y)));
}
bool cmp(node x, node y) {
	if(x.w == y.w) return x.from < y.from;
	return x.w < y.w;
}
int find(int x) {
	return x == fa[x] ? x : fa[x] = find(fa[x]);
}
int main() {
	n = read(), m = read();
	for(int i = 1; i <= n; i++) 
		E[i].x = read(), E[i].y = read();
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= n; i++) {
		for(int j = i + 1; j <= n; j++) {
			double z = jl(i, j);
			add(i, j, z);
		}
	}
	for(int i = 1; i <= m; i++) {
		int x = read(), y = read();
		add(x, y, 0.0);
	}
	sort(e + 1, e + 1 + cnt, cmp);
	for(int i = 1; i <= cnt; i++) {
		int fx = find(e[i].from), fy = find(e[i].to);
		if(fx != fy) {
			fa[fx] = fy;
			sum++;
			ans += e[i].w;
		}
		if(sum == n - 1) break;
	}
	printf("%.2lf\n", ans);
	return 0;
}