蒟蒻の并查集学习总结
定义
一种方便查找的树形结构,善于解决很多复杂的查找问题
并查集适合维护具有非常强烈的传递性质,或者具有 连通集合性质,传递性质和 连通集合性质。
基本操作
f i n d ( x ) find(x) find(x):寻找结点x的父结点
m e r g e ( x , y ) merge(x,y) merge(x,y):合并x和y至一棵树
模板
C o d e 1 Code1 Code1:初始化
void init(){//假设所有的点都没有子节点
for(int i=1;i<=n;i++){
fa[i]=i;//fa数组用于存放结点的父结点
}
}
C o d e 2 Code2 Code2: f i n d find find函数
int find(int x){
if(fa[x]==x){
return x;//如果x没有子节点,则直接返回
}else{
return fa[x]=find(fa[x]);//反之,递归寻找x的父结点,并进行记忆化(将目前搜索到的父结点存进fa[x])
}
}
C o d e 3 Code3 Code3: m e r g e merge merge函数
void merge(int x,int y){
int dx=find(x);
int dy=find(y);
if(dx!=dy){
fa[dx]=dy;
}
}
C o d e 4 Code4 Code4:完整并查集代码(具体题面见P3367 【模板】并查集)
#include<bits/stdc++.h>
using namespace std;
int n,m,fa[200010];
void init(){
for(int i=1;i<=n;i++){
fa[i]=i;
}
}
int find(int x){
if(fa[x]==x)return x;
else return fa[x]=find(fa[x]);
}
void merge(int x,int y){
int r1,r2;
r1=find(x);
r2=find(y);
fa[r1]=fa[r2];
}
int main(){
cin>>n>>m;
init();
for(int i=1;i<=m;i++){
int x,y,z;
cin>>z>>x>>y;
if(z==1){
merge(x,y);
}else{
int w1,w2;
w1=find(x);
w2=find(y);
if(w1==w2){
cout<<"Y\n";
}else{
cout<<"N\n";
}
}
}
return 0;
}
例题
一、P1551 亲戚
由题意可得:
x、y是亲戚,y、z是亲戚,那么x、z就是亲戚
这就是一个明显的树形结构(见图1-1),
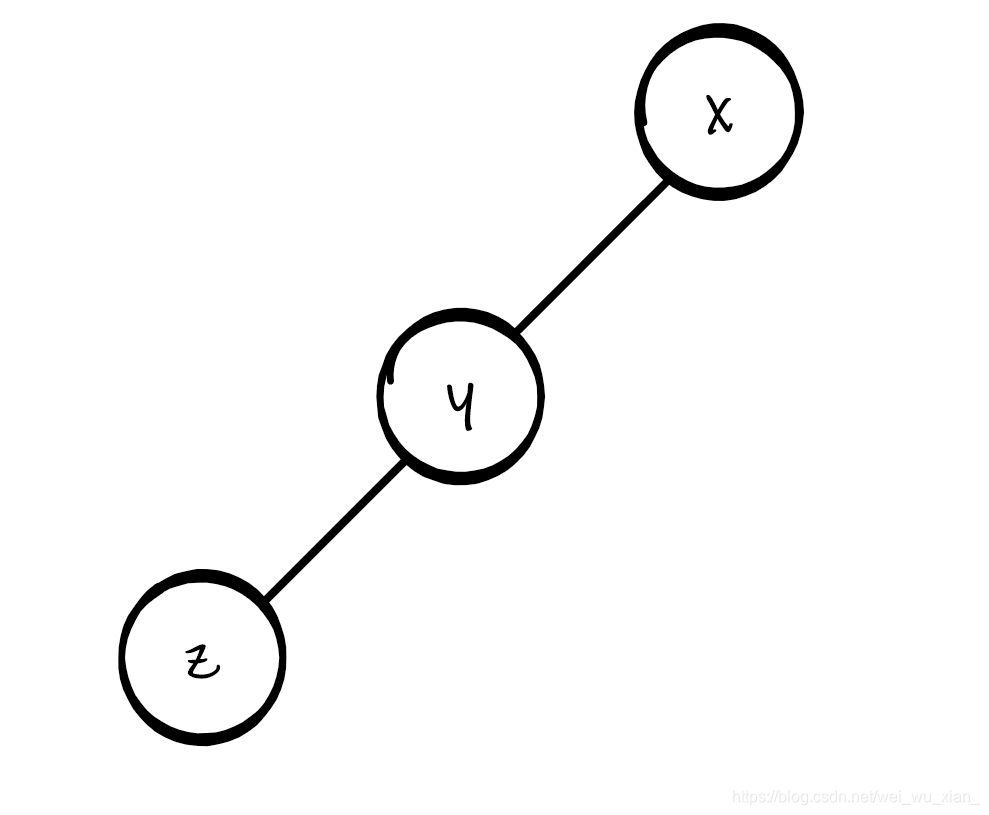
但是直接用树,时间复杂度和空间复杂度难免十分大(因为在树内查找需要使用递归遍历,容易爆栈)。
这时候并查集就发挥了巨大的作用
思路:
先将fa数组初始化,然后处理输入的m组亲戚关系,每输入一组亲戚关系,就将亲戚关系放进相应的并查集内。
最后处理输入的p组询问,每输入一组询问,就判断这两个点是否在一个并查集内,是则输出“Yes”,反之输出“No”。
T
i
p
Tip
Tip:这是一道并查集的新手入门模板题qwq
C o d e Code Code:
#include<bits/stdc++.h>
using namespace std;
int n,m,p,x,y;
int fa[5010];
int find(int x){
if(fa[x]==x)return x;
else return fa[x]=find(fa[x]);
}
void merge(int x,int y){
int dx=find(x);
int dy=find(y);
if(dx!=dy){
fa[dx]=dy;
}
}
int main(){
cin>>n>>m>>p;
for(int i=1;i<=n;i++){
fa[i]=i;
}
for(int i=1;i<=m;i++){
cin>>x>>y;
merge(x,y);
}
for(int i=1;i<=p;i++){
cin>>x>>y;
if(find(x)==find(y)){
cout<<"Yes\n";
}else{
cout<<"No\n";
}
}
return 0;
}
二、智算之道初赛第二场 - 青少组
T3 情报站(部分借鉴自智算之道-第二场初赛-题解)
题目描述
现在我方已经查明,敌人通信所使用的加密方式依赖于一个长度为 n n n 的数列,只要得知了这个数列中每个数的值,我方便可破解敌方的通信。
通过深入敌人内部的内线人员的艰苦奋斗,我方逐渐获得了一些有用的情报,通过这些情报,整个数列正在被不断地破解。
先后有 m m m 条情报被得知,每条情报是以下两种情况之一:
情况 1 1 1:知道了数列中第 x x x 个数的值
情况 2 2 2 :知道了数列中第 x x x 个数和第 y y y 个数的和
每得知一条情报,我方都试图破解数列中元素的值
作为情报部门核心技术人员的你,请编程实现如下功能:每次得知一条新情报,你都要计算当前已经能够确定出数列中的多少个数了
你比较笨,对于情况 2 这种情报,只能在已知其中一个数的情况下推出另一个数,不能通过若干情况 2 的情报列方程求解
输入格式
第一行,两个正整数 n , m n,m n,m
接下来 m m m 行,每行的第一个数是 t y p e type type
如果 t y p e = 1 type=1 type=1,则接下来跟着一个整数 x x x,表示得知了数列中第 x x x 个数的值;
如果 t y p e = 2 type=2 type=2,则接下来跟着两个空格隔开的整数 x , y x,y x,y,表示得知了第 x x x 个数和第 y y y 个数的和
输出格式
输出 m m m 行,每行包含一个非负整数,第 i i i 行的非负整数表示在得知了前 i i i 条情报之后数列中已经能够确定的数的数量
数据规模与约定
对于 20 % 20\% 20% 的数据, 1 ≤ n , m ≤ 10 1≤n,m≤10 1≤n,m≤10,且只有第一种情报
对于 50 % 50\% 50% 的数据, 1 ≤ n , m ≤ 5000 1≤n,m≤5000 1≤n,m≤5000
对于 100 % 100\% 100% 的数据, 1 ≤ n , m ≤ 3 × 1 0 5 1≤n,m≤3×10^5 1≤n,m≤3×105
可能会有重复的情报,也可能出现 x = y x=y x=y 的情况
样例输入
5 4
1 1
1 2
2 2 3
2 1 3
样例输出
1
2
3
3
思路
如果 t y p e = 1 type=1 type=1, x x x所属的集合的所有元素都能得到结果,上次的答案加上该集合的大小即是这次的答案
如果 t y p e = 2 type=2 type=2, 就把 x x x和 y y y所属的集合并起来,如果有一个集合答案已知,答案则加上另一集合的大小
C o d e Code Code:
#include<bits/stdc++.h>
using namespace std;
bool vis[300005];
int fa[300005];
int size[300005];
int n,m,ans;
int type,x,y;
void init(int n){
for (int i = 1; i <= n; i++){
fa[i] = i;
size[i] = 1;
}
}
int find(int x){
if (fa[x] != x){
fa[x] = find(fa[x]);
}
return fa[x];
}
void merge(int x,int y){
fa[fx] = fy;
size[fy] += size[fx];
}
int main(){
scanf("%d%d", &n, &m);
init(n);
while (m--){
scanf("%d", &type);
if (type == 1){
scanf("%d", &x);
int fx = find(x);
if (!vis[fx]){
vis[fx] = true;
ans += size[fx];
}
}else if (type == 2){
scanf("%d%d", &x, &y);
if (x == y && !vis[x]){
int fx = find(x);
if (!vis[fx]){
vis[fx] = true;
ans += size[fx];
}
}else{
int fx = find(x), fy = find(y);
if (fx != fy){
if (vis[fx] && !vis[fy]){
ans += size[fy];
vis[fy] = true;
}else if (!vis[fx] && vis[fy]){
ans += size[fx];
vis[fx] = true;
}
merge(fx,fy);
}
}
}
printf("%d\n", ans);
}
return 0;
}

