蒟蒻の常用排序算法总结
参考题单:洛谷【算法1-2】排序
update:2020/10/05 增加基数排序
有比较的排序
冒泡排序
基本思想
两个数比较大小,较大的数下沉,较小的数冒起来、
过程
比较相邻的两个数据,如果第二个数小,就交换位置
从后向前两两比较,一直到比较最前两个数据。最终最小数被交换到起始的位置
继续重复上述过程,依次将第2.3…n-1个最小数排好位置

时间复杂度
平均为 O ( n 2 ) O(n^2) O(n2)
C o d e 1 Code_1 Code1 未优化
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10010];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
if(a[i]<a[j]){
swap(a[i],a[j]);
}
}
}
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
return 0;
}
C o d e 2 Code_2 Code2 优化
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10010];
bool f;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
f=false;
for(int j=1;j<=i;j++){
if(a[i]<a[j]){
f=true;
swap(a[i],a[j]);
}
}
if(!f){
break;
}
}
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
return 0;
}
例题
P1116 车厢重组
思路
使用冒泡排序思想,每交换一次cnt+1,最后输出cnt即可
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10010];
int cnt;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
if(a[i]<a[j]){
swap(a[i],a[j]);
cnt++;
}
}
}
cout<<cnt;
return 0;
}
插入排序
基本思想:
在要排序的一组数中,假定前n-1个数已经排好序,现在将第n个数插到前面的有序数列中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
过程:
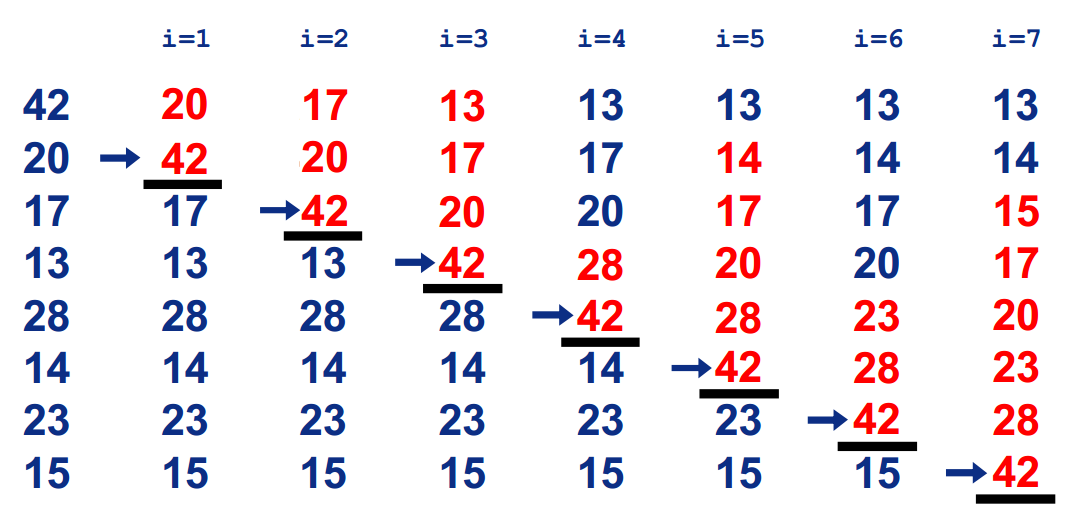
时间复杂度
平均为 O ( n 2 ) O(n^2) O(n2)
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
int n,a[110];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<n;i++){
for(int j=i+1;j>0;j--){
if(a[j]<a[j-1]){
swap(a[j-1],a[j]);
}else{
break;
}
}
}
for(int i=1;i<=n;i++){
printf("%d ",a[i]);
}
return 0;
}
选择排序
基本思想:
在长度为N的无序数组中,第一次遍历n-1个数,找到最小的数值与第一个元素交换;
第二次遍历n-2个数,找到最小的数值与第二个元素交换;
……
第n-1次遍历,找到最小的数值与第n-1个元素交换,排序完成。
过程
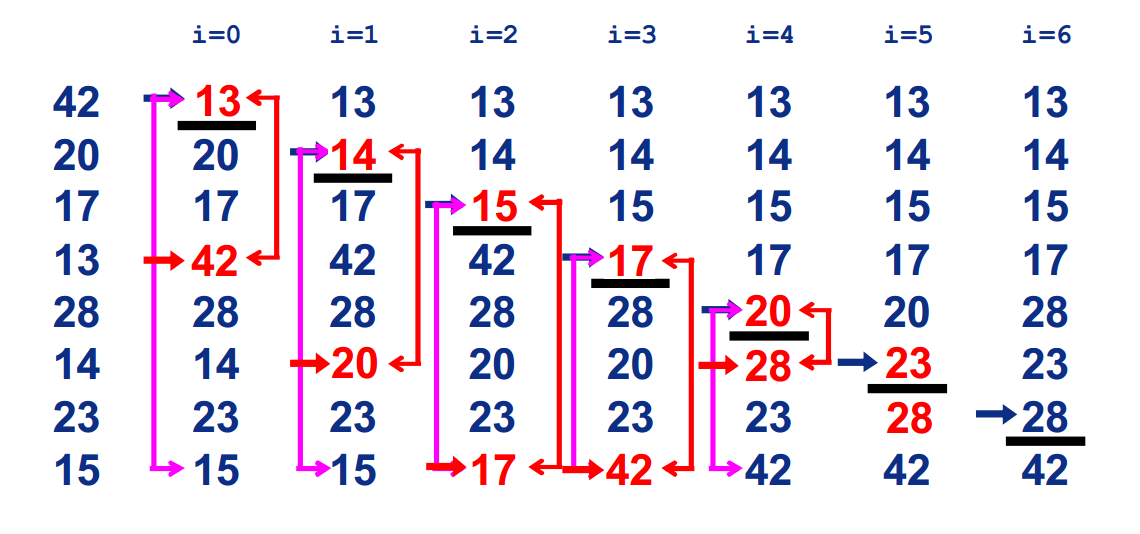
时间复杂度
平均为 O ( n 2 ) O(n^2) O(n2)
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
int n,a[110];
int p;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<n;i++){
p=i;
for(int j=i+1;j<=n;j++){
if(a[j]<a[p]){
p=j;
}
}
if(p!=i){
swap(a[i],a[p]);
}
}
for(int i=1;i<=n;i++){
printf("%d ",a[i]);
}
return 0;
}
归并排序
基本思想:
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。
首先考虑下如何将2个有序数列合并。这个非常简单,只要从比较2个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。
过程
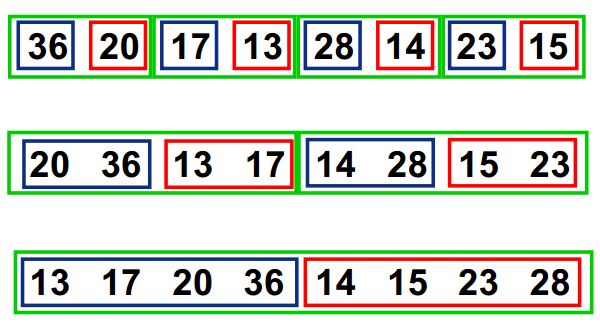
时间复杂度
平均为 O ( n log n ) O(n\log{n}) O(nlogn)
C o d e Code Code
void inversion(int *c,int l,int mid,int r){
int i=l,j=mid+1,k=l;
while(i<=mid&&j<=r)
if(c[i]<=c[j])d[k++]=c[i++];
else{
d[k++]=c[j++];
}
while(i<=mid)
d[k++]=c[i++];
while(j<=r)
d[k++]=c[j++];
for(i=l;i<=r;i++)
c[i]=d[i];
}
void merge(int *c,int l,int r){
if(l<r){
int mid=(l+r)/2;
merge(c,l,mid);
merge(c,mid+1,r);
inversion(c,l,mid,r);
}
}
例题
见“逆序对题解”
快速排序
基本思想:
- 先从数列中取出一个数作为key值;
- 将比这个数小的数全部放在它的左边,大于或等于它的数全部放在它的右边;
- 对左右两个小数列重复第二步,直至各区间只有1个数。
时间复杂度
平均为 O ( n log n ) O(n\log{n}) O(nlogn)
C o d e Code Code
void quickSort(int a[],int l,int r){
if(l>=r)
return;
int i = l; int j = r; int key = a[l];//选择第一个数为key
while(i<j){
while(i<j && a[j]>=key)//从右向左找第一个小于key的值
j--;
if(i<j){
a[i] = a[j];
i++;
}
while(i<j && a[i]<key)//从左向右找第一个大于key的值
i++;
if(i<j){
a[j] = a[i];
j--;
}
}
//i == j
a[i] = key;
quickSort(a, l, i-1);//递归调用
quickSort(a, i+1, r);//递归调用
无比较的排序
桶排序
基本思想:
首先创建数组A[MaxValue];然后将每个数放到相应的位置上(例如17放在下标17的数组位置);最后遍历数组,即为排序后的结果。
过程
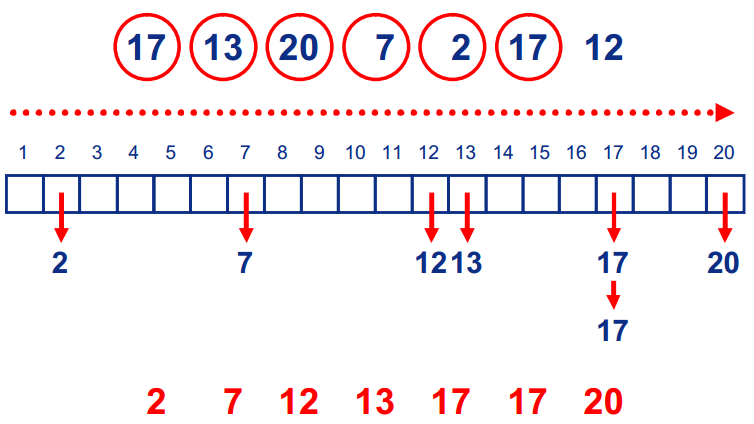
时间复杂度
平均为 O ( n ) O(n) O(n)
空间复杂度
当序列中存在较大值时,BinSort 的排序方法会浪费大量的空间开销。
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
int n,a[110],x;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&x);
a[x]++;
}
for(int i=1;i<=100;i++){
while(a[i]!=0){
printf("%d ",i);
a[i]--;
}
}
return 0;
}
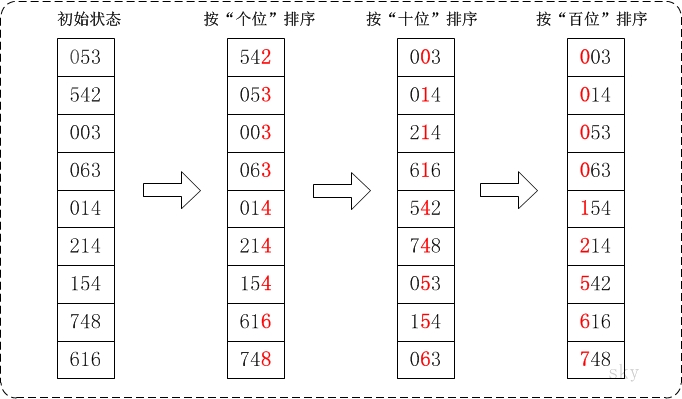
基数排序
基本思想:
将整数按位数切割成不同的数字,然后按每个位数分别比较。
过程
时间复杂度
平均为 O ( n ) O(n) O(n)
空间复杂度
大大优化了桶排序的做法,空间复杂度更小
#include<bits/stdc++.h>
#define maxn 100010
using namespace std;
typedef long long ll;
int n,a[maxn];
int Gmax(int a[],int n){
int ma=a[1];
for(int i=2;i<=n;i++){
ma=max(ma,a[i]);
}
return ma;
}
void countsort(int a[],int n,int exp){
int output[n];
int buckets[20]={0};
for(int i=1;i<=n;i++){
buckets[(a[i]/exp)%10]++;
}
for(int i=1;i<=9;i++){
buckets[i]+=buckets[i-1];
}
for(int i=n;i>=1;i--){
output[buckets[(a[i]/exp)%10]]=a[i];
buckets[(a[i]/exp)%10]--;
}
for(int i=1;i<=n;i++){
a[i]=output[i];
}
}
void radixsort(){
int exp;
int max=Gmax(a,n);
for(exp=1;max/exp>0;exp*=10){
countsort(a,n,exp);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
radixsort();
for(int i=1;i<=n;i++){
printf("%d ",a[i]);
}
return 0;
}
STL
sort
sort函数用于C++中,对给定区间所有元素进行排序,默认为升序,也可进行降序排序。sort函数进行排序的时间复杂度为 O ( log 2 n ) O(\log_{2}{n}) O(log2n),比冒泡之类的排序算法效率要高,sort函数包含在头文件为
#include<algorithm>的c++标准库中。
C o d e Code Code
#include<bits/stdc++.h>
using namespace std;
int n,a[110];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
sort(a+1,a+n+1);//sort(a+1,a+n+1,greater<int>())为逆序
for(int i=1;i<=n;i++){
printf("%d ",a[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号