线性动力学变分原理基础 Part1

线性动力学变分原理基础 Part1  《计算动力学》 张雄[著] 笔记

线弹性动力学的控制方程（位移法，要得到的是位移分量的表达式$u=u(x,y,z,t),v=v(x,y,z,t),w=w(x,y,z,t)$）

运动方程           

$\sigma _{ij,j}+\bar{f_i}=\rho \ddot u_i$

应变-位移关系     

$\epsilon_{ij}=\frac{1}{2} (u_{i,j}+u_{j,i})$

应力-应变关系   

$\sigma _{ij}=D_{ijkl}\epsilon_{kl}$

边界条件           

$\sigma _{ij}n_j=\bar{T_i}$

$u_i=\bar{u_i}$

初始条件           

$u_i | _{t=0}=\bar{u}_i^0$

$\dot{u}_i | _{t=0}=\dot{\bar{u}}_i^0$

 

精确解：在域内任一点任一时刻满足运动方程，在力边界上任一点任一时刻满足力边界条件，（位移法，位移边界条件自动满足）

近似解：加权余量法

 

加权余量法

近似解不能精确满足运动方程和力边界条件，存在余量$R_i(x,y,z,t),\bar{R_i}(x,y,z,t)$

$R_i=\sigma _{ij,j}+\bar{f_i}-\rho \ddot u_i \not=0$

$\bar{R_i}=\sigma _{ij}n_j-\bar{T_i} \not=0$

加权余量法（WRM）允许运动方程和边界条件在各点存在余量，但要求这些余量在域内和边界上的加权（对权函数）积分等于零

余量方程：

$\int_V R_i v_i dV=0$

$\int_{S_\sigma} \bar{R_i} \bar{v_i} dS=0$

$v_i$和$\bar{v_i}$分别是定义在域内和边界上的权函数（test function），权函数是任何相互独立的完备函数集

余量方程表示$R_i$与$v_i$正交，$\bar{R_i}$与$\bar{v_i}$正交

若余量方程对任意权函数都成立，即$R_i$与任意$v_i$正交，因为$v_i$是完备函数集，所以$R_i$与任意函数正交，则由変分学基本引理知$R_i$恒等于零，即运动方程在域内任一点任一时刻都满足，同理，边界条件在边界上任一点任一时刻都满足

（所以WRM在理论上，当试函数取得越多时，解越接近精确解，是收敛的）

由上述讨论，我们可以称余量方程为运动方程和边界条件的等效积分形式

 

到此，要具体实施WRM还不够，还有一个操作，把近似解取为一族已知函数（称为试探函数）的线性组合，这样就把偏微分方程变成了关于试探函数的系数的代数方程

$u_i=\sum_{i=1}^N \phi _i a_i$

$a_i$是待定参数，由余量方程确定，$\phi _i$是已知的试探函数（trial function），试探函数取自线性独立的完全的函数序列 ，试探函数的选取还需满足位移边界条件

WRM的实施是通过选择合适的待定参数强迫余量在某种平均意义下为零

 

选择不同的权函数就得到不同的WRM，下面假设力边界条件是满足的，只考虑域内余量

 

1. 配点法

权函数取Dirac函数$W_i= \delta (x-x_i),i=1,2,...,N$

代入余量方程，根据Dirac函数的性质得

$R_i(x_j)=0, i=1,2,3;,j=1,2,...,N$

这种方法相当于简单地强迫余量在域内的N个离散点（配点）上为零

 

2. 子域法

 

3. 最小二乘法

 

4. 伽辽金法

伽辽金法的权函数与试探函数相同，即

$W_i=\phi _i$

相应的余量方程：

$\int_V R_i \phi _j dV=0, i=1,2,3;j=1,2,...N$

 在许多情况下，伽辽金法得到的求解方程的系数矩阵是对称的，所以在用WRM建立有限元格式时主要用伽辽金法

当存在相应泛函时，伽辽金法与变分法往往给出同样的结果

 

例子：

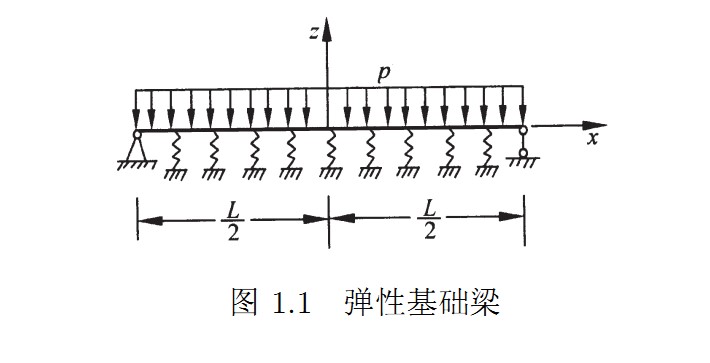
 控制方程和边界条件：

$EI\frac{d^4w^*}{dx^{*4}}+kw^*+p=0$

$w^*(L/2)=0$

$w^*(-L/2)=0$

无量纲化

$x=\frac{x^*}{L/2},w=\frac{w^*}{pL^4/EI},\alpha =\frac{k^*L^4}{16EI}$