面向对象第一单元总结
oo第一单元总结
目录
- 第一次作业
基本思路
类介绍
度量分析 - 第二次作业
基本思路
新引入的类介绍
度量分析
bug分析 - 第三次作业
基本思路
新引入的类介绍
度量分析
bug分析 - 发现他人bug的策略
- 架构设计体验
- 心得体会
第一次作业
基本思路
1.将输入的表达式经过预处理去除空格;
2.Lexer分析输入字符的语义;
3.Parser类通过递归将输入变成Expr->Term->Factor的形式,Factor包括数字和X,expr三种;
4.将Factor用一个单项式(Monomial)结构表示,包含指数和系数两个属性;
5.Term可以看成Factor相乘,系数相加指数相乘即可得到整个Term的一个单项式表达,Expr转化为Term相加的形式,即Exper以多项式的形式表示;
6.通过遍历最终得到的多项式表达,读取每个单项式(Term_poly)的系数和指数信息对应输出即可;
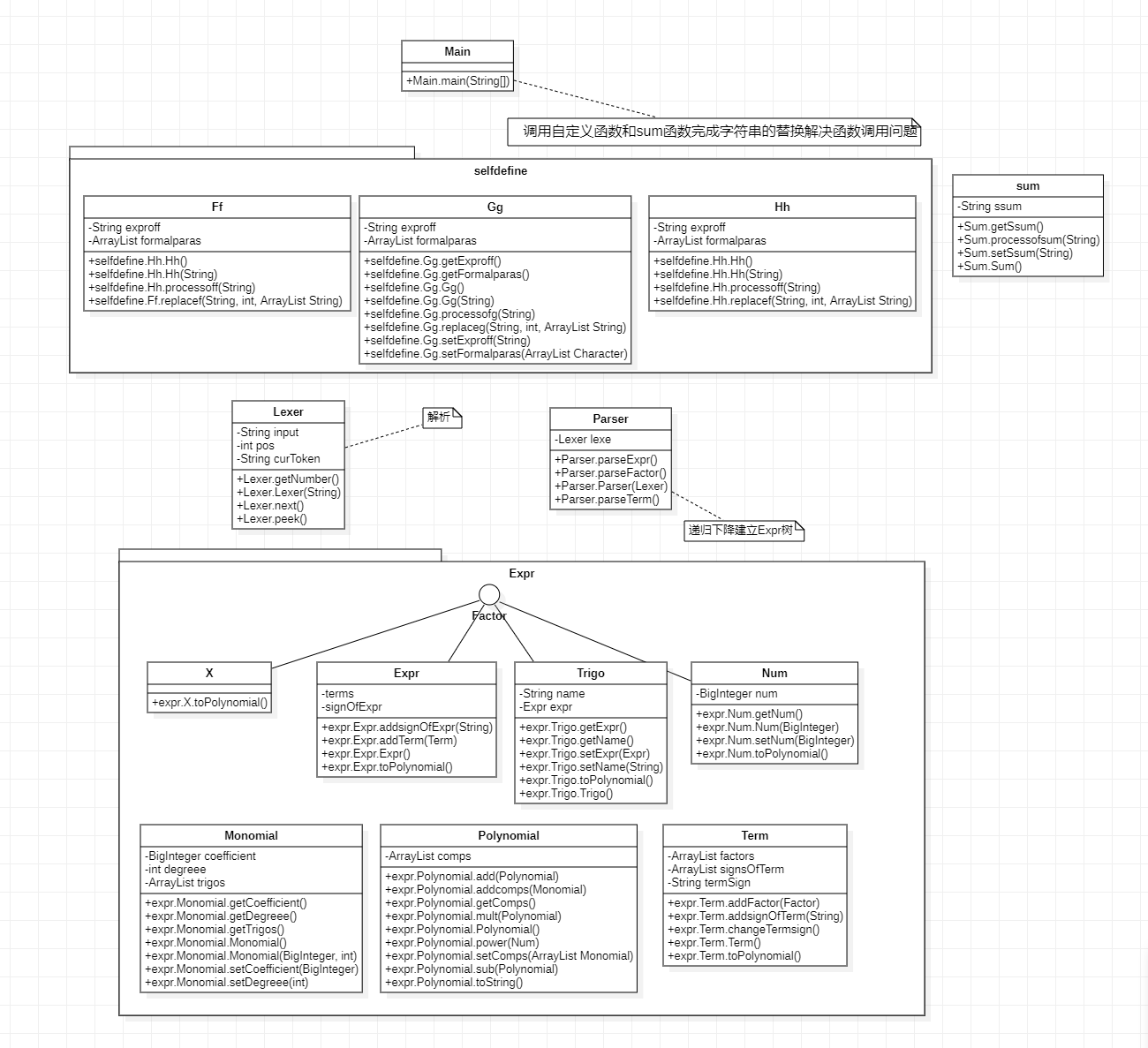
具体实现———各个类的介绍
- lexer
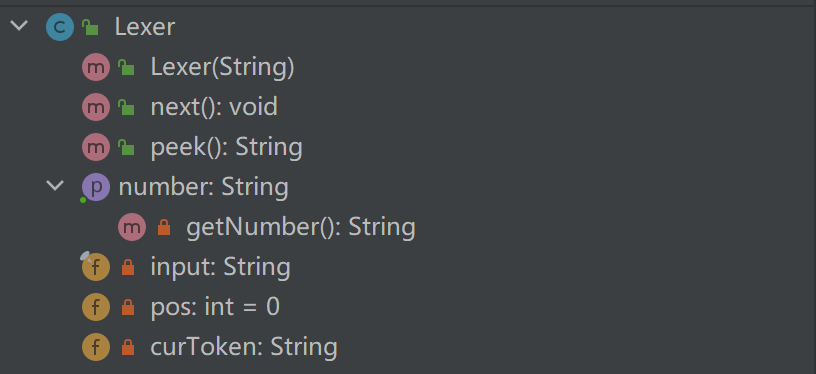
- 读取并返回数字、+-()x等给Parser
- Paser
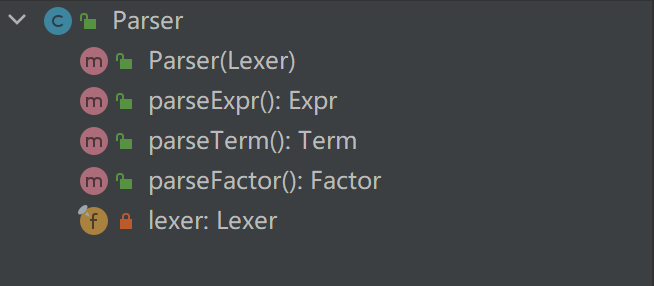
- 使用递归下降的方法依次对Exper,Term,Factor进行处理
- 对于(返回对 ()内expr的递归下降处理结果
- Factor

- 因子类接口,toPolynomial方法将因子转化为多项式的形式
- X
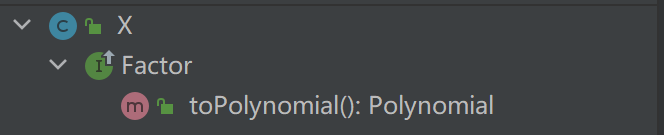
- 转化为系数为1指数为1的多项式形式
- Num
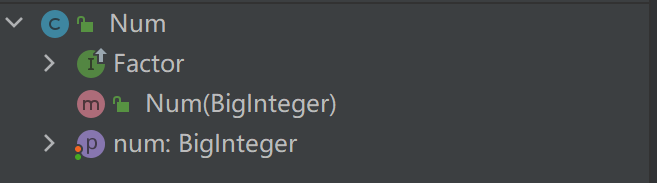
- 转化为系数为Num,指数为0的多项式形式
- Term

- 由于Term是多个Factor相乘的形式,故将Term转化为多项式形式只需要将Factor的多项式形式相乘(指数相加,系数相乘)即可;
- Expr
- 由于Expr是多个Term相加/减的形式,只需要将每个Term的多项式形式(实际为单项式结构)存储到多项式结构中即可(加入comps);
- Monomial

- 记录单项式结构的系数和指数信息,并提供getter和setter方法;
- Polynomial
- 定义多项式的加、减、乘、乘方运算
- 采用递归下降的方式将多项式转化为String类型输出;
- Main

- 进行字符串的预处理和整体流程的实现;
基于度量分析程序结构
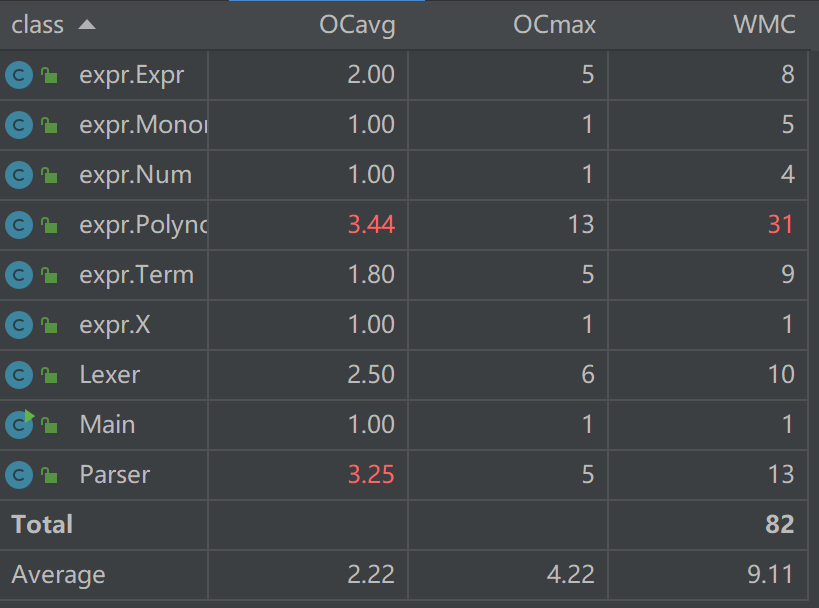
1.总代码规模分析

2.方法复杂度分析

3.类复杂度分析
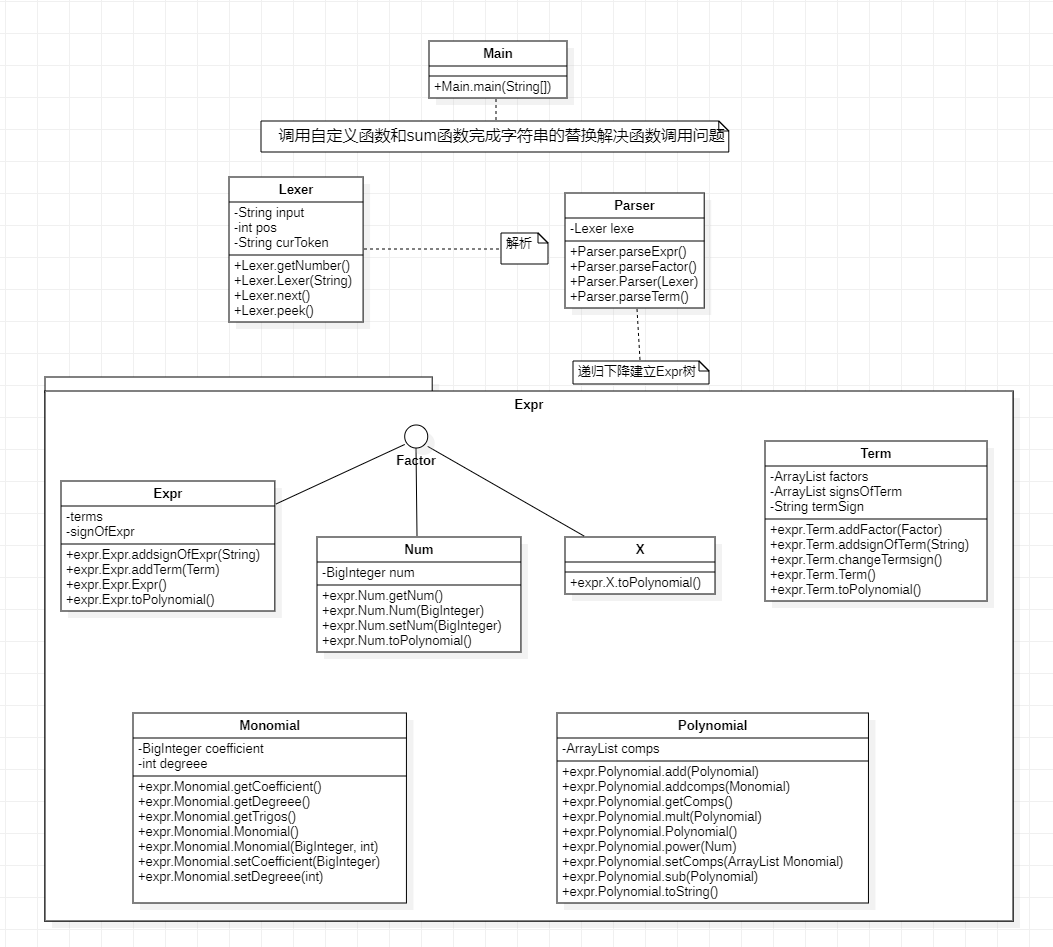
4.UML类图
5.优缺点分析
- 优点:
- 采用了递归下降的方式处理表达式,解决了多层括号的问题;
- 结构较为清晰,便于之后的迭代工作
- 缺点:
- 一些化简没有考虑到,比如非负项放在前面等;
第二次作业
基本思路
1.多层括号嵌套 √
2.引入了三角函数
在原本的结构中,多项式由多个单项式构成,这点仍然不变,我们需要改变的只是在单项式中增加三角函数项;而本次迭代过程之中,三角函数中的因子只能是x或者num,于是三角函数可以用一个包含了三角函数name(sin/cos)、三角函数的指数,三角函数(系数,指数)的Trigo类表示,而在一个单项式中可能有多个三角函数项因子,直接用ArrayList存储每个Trigo对象;
3.引入了自定义函数和求和函数
直接采用字符串替换的方法,在预处理阶段将sum和自定义函数替换掉;
新引入的类介绍
- selfdefine——Ff,Gg,Hh
- 记读入的表达式为expreoff(=右侧的部分)
- 从=左侧表达式中找到形参并记录形参个数
- 记录我们要替换的f()为str1
- 从str1中得到我们要替换的实参并储存
- 将expreoff中的形参替换为实参得到目标字符串str2(str2外面要嵌套一层括号)
- sum

- 查找sum
- 读入begin和end
- 读入表达式
- 将表达式中的i换成num(begin~end),中间用+连接
- 重复以上结果直到没有sum
- sin/cos

- 输入一个sin()/cos()字符串,提取三角函数整体的指数 、三角函数内部因子的指数和系数、三角函数的种类信息,将其转化为多项式形式-toPolynomial
- Trigo

- 将sin、cos合并成一类,便于之后的处理
- (修改)Lexer
- 增加对三角函数的识别处理,如果为三角函数则读入整个三角函数并返回Parser
- (修改)Parser
- 若识别到三角函数类,调用相应的三角函数方法生成三角函数因子
- (修改)Main
- 添加读入自定义函数的功能
- 记录自定义函数,并进行自定义函数和sum函数的替换
- (修改)Monomial
- 增加Trigo数组
- (修改)Polynomial
- 输出处理时,遍历每个单项式所有的trigos输出对应三角函数
基于度量分析程序结构
1.总代码规模分析
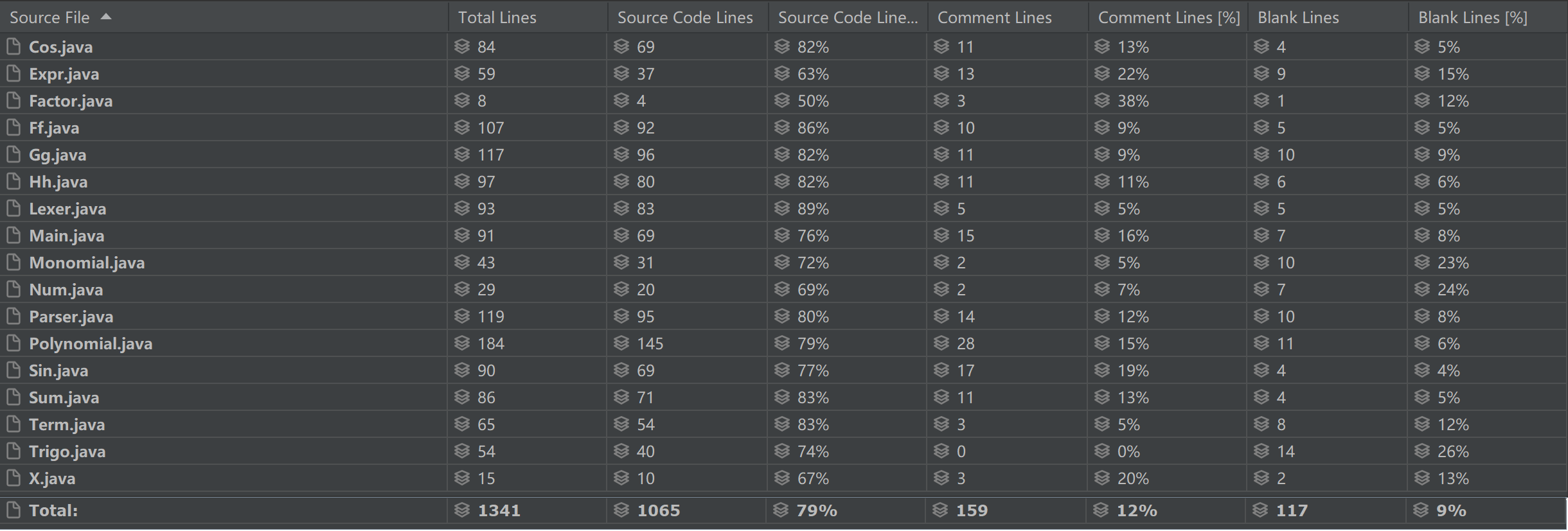
2.方法复杂度分析

3.类复杂度分析

4.UML类图
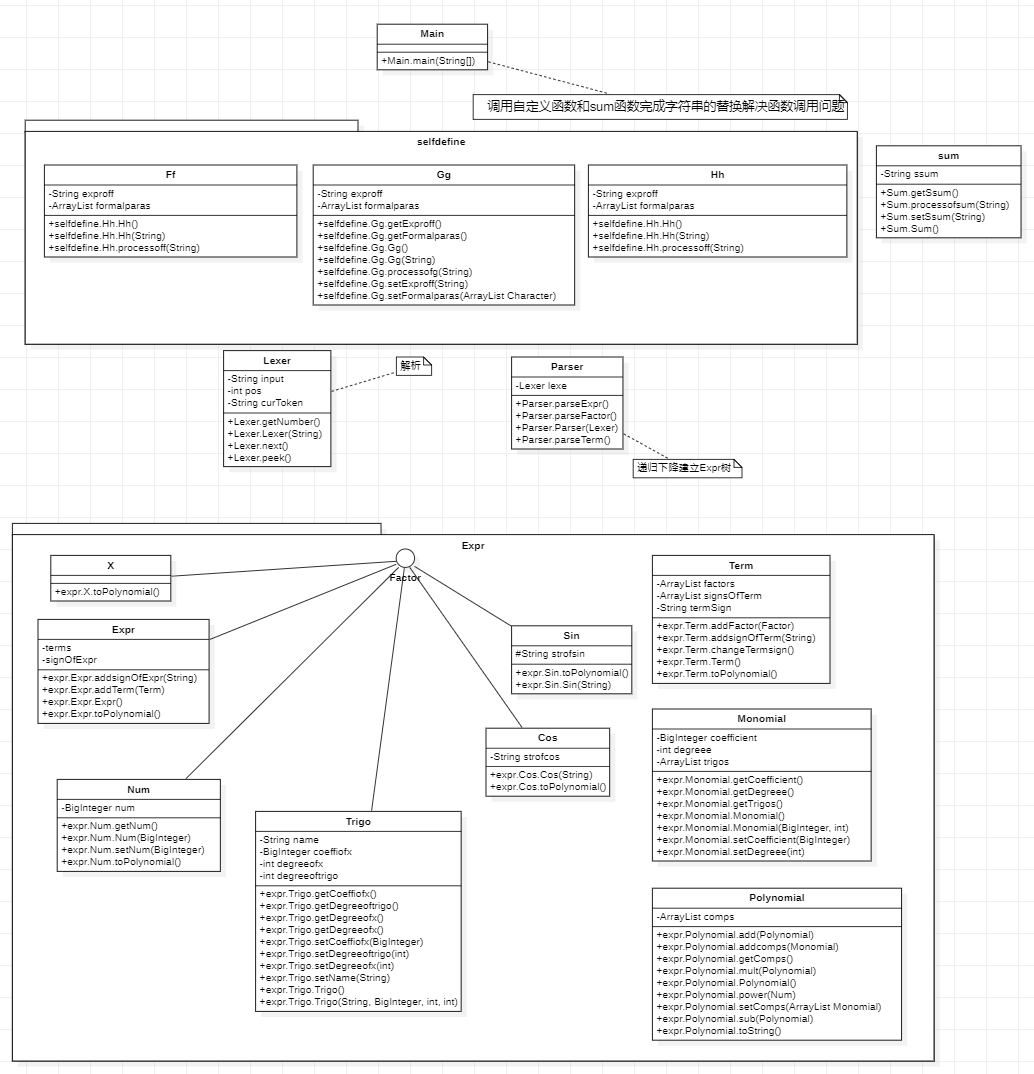
5.优缺点分析
- 优点:
- 基本保留了原有框架
- 缺点
- 简单粗暴地将三角函数括号中的因子用系数和指数形式表示,虽然解决了第二次作业的需求,但面对第三次作业的嵌套表达式时只能选择部分重构
bug分析
- 中测直接过了,所以没再测试更多的数据,这也导致了一些很严重的bug没有被发现,三角函数在进行括号内因子的识别时没有考虑因子的带符号问题,sum函数中begin和end的识别也没有识别符号;
第三次作业
基本思路
1.三角函数中嵌套表达式因子
- 删除sin和cos类,直接在Trigo类中新增一个Expr属性,存储三角函数内部的因子
- 相应的,在Lexer中识别到三角函数后,返回Parser,应递归识别三角函数括号内部的expr,并新建一个Trigo对象,记录Trigo的种类(name)以及expr;
- Monomial保持含有Trigo对象数组不变,可直接添加,只需要在输出时,将三角函数括号内的Expr通过转化为Polynomial的形式去掉括号,直接同Expr输出即可 ;
2.自定义函数可以相互(以及自身)调用
- 仍然沿用自定义函数调用的方法,不断在 input中查找f,g,h,直至处理完的字符串中不再存在自定义函数为止;
3.自定义函数可调用sum函数
- 因为sum函数不存在调用其他函数 ,所以将sum的替换放在最后,统一替换掉sum;
新引入的类介绍
- (修改)Polynomial
- 主要修改在输出部分,在遍历trigos时,输出trigo‘s name + trigo.exprtoPolynomial
- (修改)Trigo
- 增加expr属性,新建一个Trigo对象,将识别的expr赋值给Trigo.expr,即构成了一个Trigo Factor
- (修改)Main
- 循环查找字符串中的f,g,h,然后进行替换,直至字符串中没有自定义函数出现
- (修改)Paser、Lexer
- Lexer仅识别到sin/cos然后将其返回到Parser类
- Parser新建一个Trigo对象 ,存储相关信息
基于度量分析程序结构
1.总代码规模分析
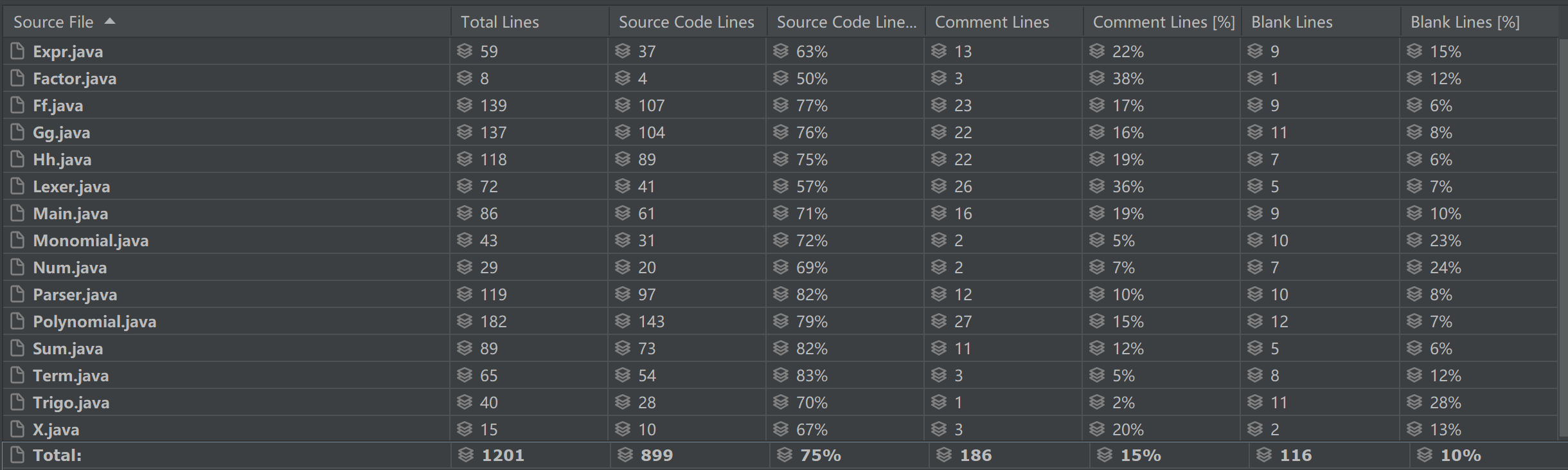
2.方法复杂度分析
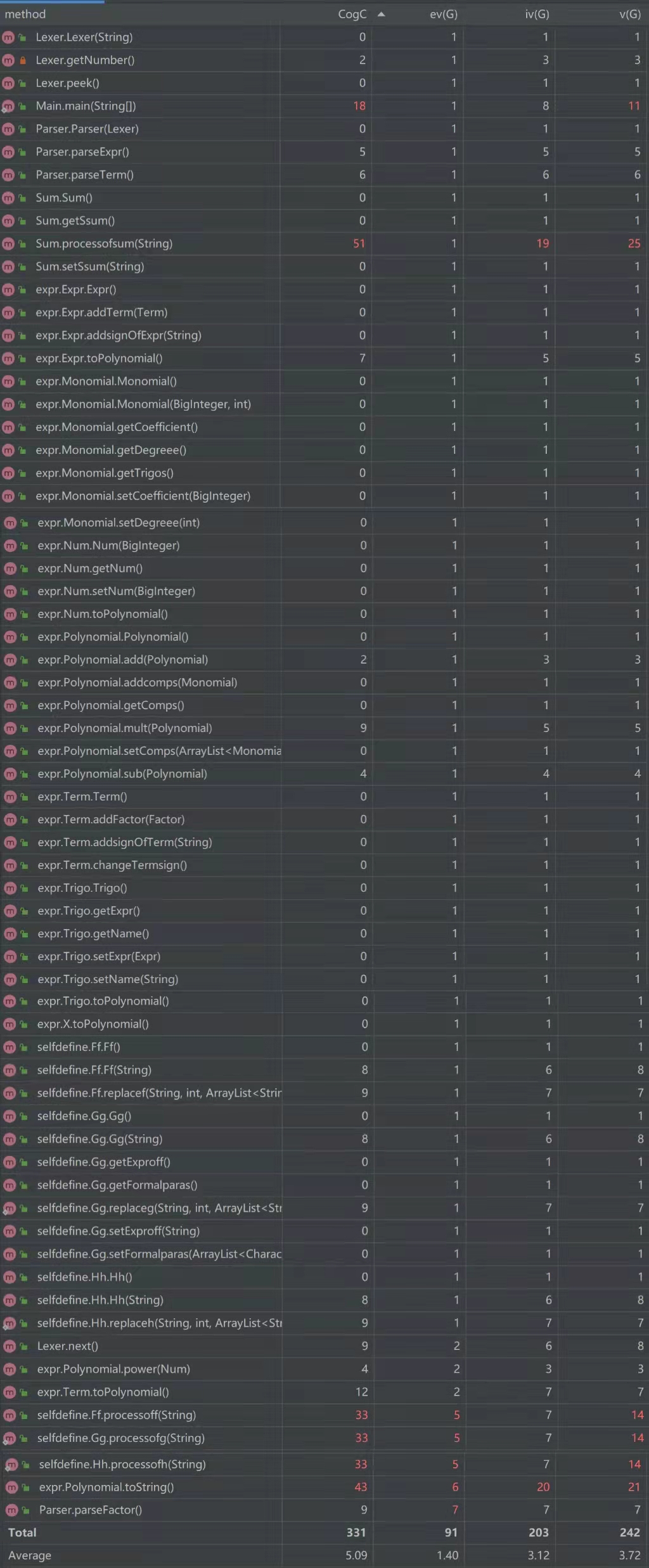
3.类复杂度分析

4.UML类图
5.优缺点分析
- 优点
- 结构较清晰,每一个类负责的功能和模块清晰,便于理解或复盘;
- 缺点
- 未进行化简优化;
bug分析
- sum函数之前遗留的bug
- 将数字直接代入时数字两边也应该要嵌套一层括号,不然就会出现 k**2(k=-1) =-1的情况
- begin 和 end 的数据类型应该为BigInterger
- 每次查找sum的位置不应该是上次查找位置+1,因为替换过后整个字符串长度会变,可能有一些sum无法识别到,每次识别位置都应该是0;
发现他人bug的策略
- 通过对基础因子的类型进行分析,尝试对带+—和前导零等因子进行测试
- 尝试“边界数据”,测试定义的数据类型是否合理
- 结合自己的易错点进行分析
- 在这过程直接尝试将前三种进行组合测试,并没有逐个阅读代码
架构设计体验
- 一个好的框架可以有效减少我们的工作量
- 扩展性强,迭代开发的工作量小
- 延伸性好,便于修改和增加功能
- 耦合性低,合理上一版本已经实现的功能
- 层次、结构清晰,方便定位和修改bug 也便于自己之后的复盘和迭代
心得体会
- 仔细阅读指导书
- 拿到作业要求之后仔细阅读指导书、分析需求是很重要的,草草开始可能会忽略掉一些关键信息导致之后无限的debug甚至是重构;
- 设计框架
- 在动手写代码之前必须先构建出一个基本框架,对主要的类和方法要做到心中有底,可以简单画一个逻辑图,觉得整体框架可行后再开始,这样重构的可能性就大大降低了;
- 实现方式
- 在迭代设计的时候将新增需求写下来,对于每一个新增需求我们能有怎样的处理办法,而这样的处理方式又需要我们在原有框架下做出哪些改动?在确定基本方向后进行处理可以明显提高我们的效率;
- 合理利用讨论区
- 在讨论区可以看到大家分享的思路、易错点和测试方法,在完成作业的过程中结合自己和他人的思考可以让我们少走很多弯路;



