集训【做题记录】
12/16
-
考虑贪心，假设一开始放进全是第一个背包，那么此时如果改成选放进第二、三个背包增加的价值为 \((w_{i,2}-w_{i,1}),(w_{i,3}-w_{i,1})\) 分别设为 \(a,b\)。问题转化为了选 \(V_2\) 个 \(a\)，选 \(V_3\) 个 \(b\)，使得总价值最大。
邻项交换法，交换选 \(a\) 和 选 \(b\) 的数 \((i<j)\)，则不交换时最优满足：
\[\begin{aligned}a_i+b_j&\ge a_j+b_i\\ a_i-b_i&\ge a_j-b_j \end{aligned}\]设 \(a_i-b_i=c_i\) 按照 \(c_i\) 的大小从大到小排序，则此时一定满足所有选 \(a\) 的位置都在所有选 \(b\) 的位置之前，否则通过邻项交换一定能使它们变得更优。
枚举划分点 \(k\)，在 \(k\) 之前（包括 \(k\)）选 \(V_2\) 个 \(a\)，在 \(k\) 之后选 \(V_3\) 个 \(b\)。分别预处理出在前缀中选 \(V_2\) 个最大 \(a\)，在后缀中选 \(V_3\) 个最大 \(b\) 的答案。
-
两种操作，一种是操作权值，一种是操作位置。从小到大递推，首先考虑只有一个格子的情况，奇数点必胜，偶数点必败。
进一步思考下一个必败点在哪：
-
奇数：如果操作位置到达的后继状态全是必胜态，则先手可以一直操作权值，使得后手被迫操作位置到达必胜态；如果操作位置到达的后继状态有必败态，则先手可以直接操作位置到达必败态。两种情况，恰好有一个先手必胜，结论：奇数点一定是必胜点。
-
偶数：如果操作位置到达的后继状态全是必胜态，则先手没办法操作权值，使得后手操作位置到达必胜态，此时先手必败；如果操作位置到达的后继状态有必败态，则先手可以直接操作位置到达必败态。结论：偶数点必胜，当且仅当它的后 \(k\) 个位置内有败点，否则先手必败。
既然这样，我们就知道了判断一次询问的方法。从 \(r\) 开始往前找到第一个偶点（一定是败点），再根据这个败点找到下一个败点：往前跳 \(k+1\) 步后的遇到的第一个偶点。这样不断重复，如果找到的最后一个败点是 \(l\) 则，先手必败，否则，先手必胜。
观察发现我们每次都是先往前跳 \(k+1\) 步，在跳一些步找到下一个败点。根据《弹跳绵羊》的启发，可以用分块维护，但这里每次维护的是从 \(i\) 跳到的块内最后一个败点。每次修改只有 \(x\) 为奇数的时候会改变奇偶性，散块直接暴力修改，整块直接 \(tag\oplus 1\)，分别预处理出 \(tag\) 为 \(1\) 和 \(0\) 时的值即可。
-
12/17
-
考虑把 \(x\) 到 \(y\) 路径上的字符以 \(lca\) 分成两段，由于 \(|S|\) 很小，只需统计前一段匹配了 \(S\) 中的 \((1,i)\) \(\times\) 后一段匹配了 \(S\) 中的 \((i+1,len)\) 的方案数。
设 \(f_{x,l,r}\) 表示从 \(x\) 到根节点匹配了 \(S\) 中的 \((l,r)\) 的方案数，\(g_{x,l,r}\) 表示从根节点到 \(x\) 匹配了 \(S\) 中的 \((l,r)\) 的方案数，可以 \(O(n\times |S|^2)\) 预处理得到。
怎么得到 \(x\) 到 \(lca\) 的匹配了 \((1,i)\) 的答案？考虑容斥，假设此时 \(<i\) 的答案都已得到，则 \(ans_i=f_{x,1,i}-\sum\limits_{j=0}^{i-1} ans_j\times f_{lc,j+1,len}\)，同理 \(lca\) 到 \(y\) 的答案也可以容斥得出，复杂度 \(O(q\times |S|^2)\)。
-
合法区间不多的时候，我们可以抓取出所有合法区间，然后直接 DP。
考虑怎么抓取出 \((l,r)\) 中的所有合法区间？启发式分裂，设 \((l,r)\) 中 \(b_i\) 取到最大值的位置为 \(p\)，则对于所有跨过 \(p\) 的区间，区间和的范围一定在 \(2^{b_p}\le s \le 2^{b_p}\times (r-l+1)\) 之间，即 \(2^{b_p}\le s \le 2^{b_p+\log (r-l+1)}\)。
用 \(siz\) 较小的一边去计算 \(siz\) 较大的一边，假设 \(siz\) 较小的一边在左边，即对于 \(siz\) 较小的一边每次查询是否存在一个 \(k\) 位置的前缀 \(=s_{i-1}+2^j(j\in [2^{b_p},2^{b_p+\log (r-l+1)}])\)，且 \(p\le k\le r\)。取一个大质数，处理出前缀和后用哈希表存即可。
启发式分裂带一个 \(log\)，枚举区间和带一个 \(log\)，时间复杂度为 \(O(n\log ^2 n)\)。
12/18
-
学习了启发式分裂，给定 \(n\) 个数，求满足某种条件的点对数目，而这个条件与点对 \((a,b)\) 所在区间 \([a,b]\) 的最大/最小值有关。
考虑类似于分治的形式，以最大值所在的位置划分为左区间和右区间，每次用较小的一边去计算较大的一边的贡献。本质上是一个树形结构，所以其实和树上启发式合并是一样的。
对于这道题，启发式分裂时，对于每个 \(a_i\) 查询是否有 \(a_j\le \cfrac{a_p}{a_i}\)，其中 \(p\) 为最大值取到的位置，且 \(p\le j\le r\)（假设左区间的元素少）。发现这个询问不好直接做，离线下来用扫描线扫即可。
-
对于类似的给定 \(n\) 个函数，询问 \(x\) 经过区间 \([l,r]\) 后得到的值的答案，可以采用“插入+标记+回收”的算法。
即把所有询问离线下来，在 \(l\) 处插入，在 \(r+1\) 处回收，通过一些数据结构维护标记（线段树、平衡树……）。
对于这道题，每次只需把 \(v\in [a_i,b_i]\) 的答案 \(+1\)。观察到如果按询问的插入时间排序，这些点一定是连续的一段区间，因为整个图像是单调递减的。对此，我们只需每次在线段树上二分，实现区间加和区间减即可。
-
转化题意这一步很关键，对于每个区间 \((l_i,r_i)\) 询问所有的 \(L\le l_i,r_i\le R\) 的 \((L,R)\) 区间的交集。观察到，交集即为 \(L\) 取到最大值，\(R\) 取到最小值，离线下来扫描线即可。
-
一个比较直接的思路是，对于每组询问中的每组，分别遍历区间，查询是否有点在它之内，复杂度为 \(O(TMN\log )\)，TLE 了。
其主要原因是因为 \(MN\) 太大，但是我们观察到总点数 \(\le 3\times 10^5\)，如果把 \(MN\) 替换成 \(3\times 10^5\) 肯定能过。不管是对于每一个点去枚举有哪些线段合法，还是对于每一个点枚举有哪些线段不合法，都会导致算重。考虑这是一个数轴（所有点从小到大排序），考虑哪些线段一定不合法，整条线段都被包含在两点之间的一定是不合法的，即 \(pre_i\le l\le r\le now_i\)，扫描线即可。
-
一个很关键的点是询问全局颜色数，考虑容斥，什么时候一个数是不合法的，分为两种：这个数本身在全局就没出现过也没人替补它，这个数在全局出现了但是又被删除了。
第一种情况，\(x\) 没有出现过，此时的合法区间满足对于所有的 \(pre_{x-1}<l\le r<now_{x-1}\)，即 \((l,r)\) 内没有出现过任意一个 \(x-1\)。
第二种情况，\(x\) 出现过，此时的合法区间满足对于所有的 \(pre_{x-1}<l\le l_x\le r_x\le r<now_{x-1}\)，其中 \(l_x\) 表示 \(x\) 出现的最左的位置，\(r_x\) 表示 \(x\) 出现的最右的位置。
考虑扫描线怎么扫，拿第二种情况举例，我们的询问区间 \((l,r)\) 一定满足 \(l\in(pre_{x-1},l_x]\)，\(r\in [r_x,now_{x-1})\)。用类似于差分的方法，在扫到 \(r_x\) 时把 \((pre_{x-1},l_x]\) 这个区间加一（表示 \(l\) 属于该区间时可以删掉一个数），扫到 \(now_{x-1}\) 时把 \((pre_{x-1},l_x]\) 区间减一，单点查询即可，可以用树状数组维护。
12/19
-
容易发现对于环上的点，如果要选其中的某一个，则整个环都必须选。所以该题的第一步是 tarjan 缩点，对于一个强连通分量，选该环的代价为 \(\sum V_i\)，收益为 \(\sum W_i\)
数据范围极小，考虑树形背包，设 \(f_{x,i}\) 表示 \(x\) 的子树内选了一个包含 \(x\) 的连通块（\(x\) 必须选），代价为 \(i\) 时的最大收益，直接树形背包即可，时间复杂度为 \(O(nm^2)\)
-
推式子+拆贡献：
\[\begin{aligned}f(u,v)&=\sum\limits_{x\in S(v)} dis(u,x)^2-\sum\limits_{x\notin S(v)}dis(u,x)^2\\ &=2\times \sum\limits_{x\in S(v)} dis(u,x)^2-\sum\limits_{x\in S(1)}dis(u,x)^2\\ \end{aligned}\]答案就变成了给定 \(u\)，求解一个类似 \(\sum\limits_{x\in S(t)} dis(u,t)^2\) 的式子：
\[\begin{aligned} \sum\limits_{x\in S(t)} dis(u,t)^2&=\sum\limits_{x\in S(t)} (d_u+d_x-2d_{lca})^2\\ &=\sum\limits_{x\in S(t)}(d_u^2+d_x^2+4d_{lca}^2+2d_ud_x-4d_ud_{lca}-4dxd_{lca})\\ \end{aligned}\]\(d_u^2,d_u\) 相当于常数，\(d_x^2,d_x\) 树形 DP 很好维护，麻烦的是 \(d_{lca}\) 怎么处理。两种情况，一种是 \(u,t\) 不在同一条链上，\(lca\) 一定是 \(lca(u,t)\)；一种是 \(u,t\) 在同一条链上，此时又有两种情况，\(t\) 是 \(u\) 的祖先，\(u\) 是 \(t\) 的祖先。前者直接做即可，我们来考虑后者。
对于 \(u\) 子树内的点 \(lca(x,u)\) 一定是 \(u\)，这部分也直接算即可。对于 \(t\) 子树内不是 \(u\) 子树内的节点，\(lca\) 一定是 \(u\) 到 \(t\) 链上的点，在每个点上挂上贡献，倍增处理即可。
注意这道题有边权，记录到根节点的距离需要两个数组，\(d_i\) 表示 \(i\) 到根节点的边的条数 \(+1\)，\(D_i\) 表示 \(i\) 到根节点的距离。倍增时应该用 \(d\) 数组，算贡献时应该用 \(D\) 数组。
-
首先考虑 \(O(n^3)\) 的 DP，设 \(f_{u,i}\) 表示 \(u\) 内未配对的点有多少，转移时枚举 \(f_{v,j}\)，由于 \(u\rightarrow v\) 这条路径一定得染色，所以 \(j\ge 1\)，枚举匹配对数 \(k\)，则
\[f_{u,i+j-2\times k}=f_{u,i}\times f_{v,j}\times \binom{i}{k}\binom{j}{k}\times k! \]答案即为 \(f_{1,0}\)，但这样做很复杂，时间复杂度 \(O(n^3)\)
正难则反，考虑容斥（我是说他语文渣，但没说他数学称霸啊——容斥）
答案显然为 \(\sum\limits (-1)^{|S|} T(S)\)，其中 \(S\) 是边集，\(T(S)\) 表示至少有这些边不被覆盖的方案数。
我们现在就变成了要求删掉一些边后，剩余的边染色（至少这些删掉的边没被染色）的方案数。考虑删掉一些边后，答案变成了很多连通块。一个大小为 \(n\)（\(n\) 为偶数）的连通块任意染色（即任意两两配对，不一定所有的边都染上颜色），方案数
\(g_{n}=(n-1)\times(n-3)\ldots 3\times 1\)设 \(f_{u,i}\) 表示 \(u\) 的连通块大小为 \(i\)，且不算 \(u\) 所在块内配对的方案数，转移时分两种情况讨论，带上容斥系数：
-
\(f_{u,i+j}=f_{u,i}\times f_{v,j}\)，\(u\) 和 \(v\) 之间有连边
-
\(f_{u,i}=f_{u,i}\times f_{v,j}\times(-1)\times g_j\)，\(u\) 和 \(v\) 之间没有连边
最后的答案即为 \(\sum\limits_{i=1}^n f_{1,i}\times g_i\) 注意 \(i\) 为奇数时，\(g_i\) 就等于 \(0\)。
-
-
考察二叉树的性质，每个节点最多只有两个子节点。比较显然的暴力是用 \(n\) 次询问，询问出每个点的深度，按深度从小到大枚举点，从它的上一层节点中枚举父亲，复杂度为 \(O(n^2)\) 的。
树链剖分放在二叉树上一个重要的性质就是，一个节点只有重儿子和轻儿子两条链，在我们枚举每一个点 \(x\) 时，设 \(1\) 所在重链深度最大的节点为 \(y\)，如果能知道 \((x,y)\) 的 \(lca\)，那我们就知道了 \(x\) 一定是在 \(lca\) 的两条链上，如果 \(d_x-d_lca=1\) 则 \(lca\) 就是 \(x\) 的父亲，否则 \(x\) 就应该是 \(lca\) 的轻链上点，\(y\) 变成该轻链上深度最大的点。不断循环这个过程，最后一定能找到 \(x\) 的父亲。
如何知道 \((x,y)\) 的 \(lca\)？我们可以查询出 \(x\) 到 \(y\) 的距离，根据 \(dis(x,y)=d_x+d_y-2\times d_{lca}\)，我们可以得到 \(lca\) 的深度，再根据这个深度从 \(y\) 不断往上跳，就可以找到 \(lca\) 了。在枚举每一层节点时重构树链剖分，找 \(lca\) 的过程，找 \(y\) 的过程都是 \(O(n^2)\) 的。但最多只有 \(\log n\) 条链，所以查询次数是 \(O(n\log n)\) 的。
12/20
-
从大到小按 \(q_i\) 将衣服重排，暴力思想是枚举每一个人，再枚举衣服，能选则选，复杂度 \(O(n^2)\) 的。考虑换个枚举思路，先枚举衣服，此时对于所有 \(b\ge c\) 的询问，减去 \(c\) 的贡献。可以想到用平衡树打 tag 标记维护区间减的操作，但是减去 \(c\) 的贡献后，两个值域可能有交，而朴素的 merge 实现的是值域无交合并。
两种方法：
-
对于 \(b\ge c\) 的询问，把它们分为两部分，\([c,2c),[2c,+\infty]\)，可以发现对于后半部分区间减 \(c\) 后值域与 \(b<c\) 是无交的，可以直接用 merge 合并。对于前半部分我们可以把它删除后暴力插入新点，对于这部分询问由于每次询问至少减半，所以复杂度为 \(O((n+\sum \log q_i)\log n)\)。
-
食用 Fhq-treap 有交合并，单次合并时间复杂度为 \(O(\log ^2n)\)，总时间复杂度为 \(O(n\log ^2n)\) 也可通过本题。
-
-
像这种给定多个函数，让你求区间函数复合后的结果的题，很容易想到离线后“插入+标记+回收”的思路。
由于这道题每次是 \(+y-p\) 而值域很大，所以不能使用上一道题的第一种方法。用有交合并，打 tag 标记，回收时注意要加上它到根节点路径上的所有 tag 标记，所以还需维护一个 \(fa_x\)，每次往上跳父亲。总时间复杂度为 \(O(m\log ^2 n)\)
12/21
-
引理：无向图中只有树边和返祖边，没有横插边。
二分图定义：所有点能分成两个集合，且集合内部之间没有连边。
二分图判定：不存在奇环（从一个集合到另一个集合，再回到这个集合，所经过的边数一定是偶数）
题意转化为删除一条边之后，原图不存在奇环，我们来分类讨论一下：
-
原图本就不存在奇环，说明原图是一个二分图，此时随便删边都可以。
-
原图存在奇环，称一条返祖边所覆盖的边为该环上的其它边。
-
一条奇环：可以删掉该返祖边本身，或该返祖边所覆盖的边中不被偶环返祖边覆盖的边。
-
多条奇环：应删掉所有奇环返祖边所覆盖的边的交集，且这些边不被任何偶环返祖边覆盖。
前半部分很好理解，考虑为什么不能被偶环返祖边覆盖。如果存在一条边同时被偶环和奇环返祖边覆盖，则删去这条边后，偶环的边数变为奇数，奇环的边数变为偶数，且两个环一定能合成一个更大的奇环。
-
可以把边的信息挂在点上，树上差分，对于奇环覆盖的边 \(+1\)，对于偶环覆盖的边 \(-1\)，符合条件的边当且仅当权值等于 \(cnt\)（奇环的条数），注意图不连通。
-
-
题目要求满足若 \(x\) 欠 \(y\) 钱，则 \(x\) 不能恰好在 \(y\) 之前进入办公室，但可以让 \(y\) 在 \(x\) 之前进入办公室。
由此想到按欠债关系建边后，由子节点 \(y\) 出来后再选 \(x\) 节点。
-
关于异或最大的问题，可以考虑线性基。
从 \(1\) 号节点到 \(n\) 号节点的简单路径肯定是一条链。考虑从该链上扩展，再经过某些其它的边使得异或和最大。容易发现，如果经过的边不是环，则相当于没经过（去了一趟又回来，两趟异或和为 \(0\)）。结论想要扩展一条链，一定是用一个环的权值去扩展。
启发我们把所有环的异或权值扔进线性基里，考察一个数与环异或的最大值。对于这个数我们随便选一条 \(1\) 到 \(n\) 的链即可。考虑为什么可以随便选，如果有两条 \(1\) 到 \(n\) 的链，则一定构成一个环，被放进线性基里。如果另一条链更优，则我们随便选的这条链，异或上该环则得到的是另一条更优的链。
剩下的就变成了线性基板子题。
-
原题大概可以转化成一个求 \(k\) 分图的题，需要特殊注意的是，该题为有向图。
我们先从简单的入手，如果给出的是一颗树时的答案是多少？手模一下，其实可以发现如果给出的是一颗树，则最大的 \(k\) 就等于树中直径的长度，同样的可以类推森林。
然后我们再来考虑环的情况，对于单个的环来说，其中 \(k\) 最大可能为环中的节点个数，且节点个数的所有因数都为 \(k\) 可能的取值。同理推得多个环的情况，\(k\) 最大应为所有环中节点个数的 \(gcd\)（因为所有环都要满足），最小也应为 \(gcd\) 的因数。
考虑建图：建图的时候不仅连一条 \(u\rightarrow v\) 且边权为 \(1\) 的边，同时连一条 \(v\rightarrow u\) 且边权为 \(-1\) 的边
对于每个连通块，从任意一个节点开始，经过某条边的时候就加上它的权值。第二次走到该点的权值减去第一次走到该点的权值就是该环/链的答案。
注意面具种类数最少是 \(3\)。
-
CF521E Cycling City （双倍经验）
题目要求在无向图中找出两点，使得两点之间至少有 \(3\) 条不相交路径。
我们先来思考什么样的点能有 \(3\) 条不相交的路径，大概是两条返祖边所覆盖的点的交集中，深度最大的点。（深度不是最大就会有交）充分性显而易见，考虑怎么证明其必要性。
考虑反证法，即不存在上述情况，也有满足条件的三条路径和两个点。对于不在同一条链上的点，不可能有符合条件的三条路径。对于在同一条链上的点，找不出不存在上述情况还满足条件的答案。
-
考虑对于 \(1,2\) 两种操作，由 \(i-1\) 向 \(i\) 连边，对于 \(3\) 操作，由 \(k\) 向 \(i\) 连边，这样最终得到的肯定是一棵树。对于每个节点的答案，观察发现只与它到根节点的路径上的操作有关，这样就可以用可持久化并查集维护了。
12/22
-
对于类似该题的：求前 \(k\) 大的区间异或和/区间和/两两匹配的数……都可以转化成同一种套路：贪心+堆优化+数据结构
首先对于每个 \(i\) 在优先队列里放进以它为左端点的最优答案，同时记录 \(l,r\) 表示答案在哪个区间取到，\(p\) 表示最优答案在哪个右端点取到。每次在堆里贪心的选择前 \(k\) 大即可，但是考虑到我们忽略了一些可能的答案，所以每次在取出当前堆顶后，要重新在堆中加入：以 \(i\) 为左端点，\([l,p-1]\) 中某个数为右端点；以 \(i\) 为左端点，\([p+1,r]\) 中某个数为右端点。
这道题按照上面的套路，我们要对于每个 \(i\) ，查询一个右端点使得区间异或和最大。转化成前缀异或和，就变成了在 \([l,r]\) 中找到 \(\oplus s_{i-1}\) 最大的点，可以用可持久化 Trie 树实现，时间复杂度为 \(O(n\log n)\)。
-
考虑邻项交换法：设当前两个位置 \(i,j(i<j)\)，前面所有大臣左手上的数的乘积为 \(P\)，左手上的数为 \(a_i\)，右手上的数为 \(b_i\)，则 \(i\) 排在在 \(j\) 之前一定满足：
\[\begin{aligned} \max(\cfrac{P}{b_i},\cfrac{P\times a_i}{b_j})&\le \max(\cfrac{P}{b_j},\cfrac{P\times a_j}{b_i})\\ \max(P\times b_j,P\times a_i\times b_i)&\le \max(P\times b_i,P\times a_j\times b_j)\\ \max(b_j,a_i\times b_i)&\le \max(b_i,a_j\times b_j) \end{aligned}\]由于 \(b_j\le a_j\times b_j,b_i\le a_i\times b_i\)，所以我们只需比较 \(a_i\times b_i\) 与 \(a_j\times b_j\) 的大小即可。
-
对于求解能否用几个数凑出来小于等于 \(k\) 的数，或求凑不出来的最大的数……都可以转为同余最短路求解。
首先把题目转化为前缀和，求出有多少 \(\le r\) 的数使得等式存在非负整数解减去有多少 \(\le l\) 的数使得等式存在非负整数解，然后这道题就变成了《跳楼机》，同余最短路的板子题。
设 \(dis_i\) 表示 \(\mod x=i\) 的数中，最表示的最小的数，则我们就可以统计 \(dis_i\le r\) 中，能表示的 \(\mod x=i\) 的数有多少。对于 \(u\in[0,x)\) 连一条到 \((u+a_i)\mod x\) 的边，边权为 \(a_i\)，跑最短路即可。
-
首先易于发现，如果形成了一个环的话，想要选环上的任意一点，一定得把整个环都选上，tarjan 缩点后，每个点的战斗值为该强连通分量的战斗值之和，招募费用也同理。这样就把题目转化成了树形 DP，但是题目要求一个分式的极值，考虑分数规划。
给出 \(a_i\) 和 \(b_i\)，求一组 \(w_i\in{0,1}\)，最小化或最大化
\[\cfrac{\sum\limits_{i=1}^n a_i\times w_i}{\sum\limits_{i=1}^n b_i\times w_i} \]另一种描述，每个物品有两个权值 \(a\) 和 \(b\)，选出若干物品使得 \(\cfrac{\sum a}{\sum b}\) 最小/最大
分数规划的通用方法是二分，假设我们要求一个最大值，二分一个答案 \(mid\)，则 \(mid\) 合法一定满足：
\[\begin{aligned} &\cfrac{\sum a}{\sum b}\ge mid\\ \Longrightarrow&\sum a\ge mid\times \sum b\\ \Longrightarrow&\sum a\ge \sum b\times mid\\ \Longrightarrow&\sum (a-b\times mid)\ge 0 \end{aligned}\]把权值转化为了 \(a-b\times mid\)，选一些点使得权值和最大。如果最大值要大于等于 \(0\)，则说明 \(mid\) 合法，否则不合法。
由于题目给出的可能是是森林，我们考虑建一个虚点 \(0\)，向所有连通块连一条边。设 \(f_{i,j}\) 表示必须选 \(i\) 时，\(i\) 的子树内选了 \(j\) 个点的最大贡献。
-
感觉这道题解法挺巧妙的，跟枚举矩形时枚举对顶角挺像的。
\(O(n^2)\) 枚举中间两个点，check 是否存在合法路径。具体的，\(O(n^2\log m)\) 对每个点跑一遍 dij，对于每个点处理出距离它 \(\le k\) 的前三个权值最大的点（且能在 \(k\) 步之内到达 \(1\)）。处理出前三个是考虑到会有重复的点出现，如果弄不清楚可以根据实际情况调到复杂度合理的范围之内，保证结果正确性就行。
-
由于每个节点是一个数，可能会有重复，而我们要求的是本质不同的数，且 \(a_i,b_i\le n\)。把选与不选的关系转化为图，对 \(a_i\) 向 \(b_i\) 连一条无向边。如果连出来是一颗树，我们手模发现答案即为 \(siz-1\)（考虑对于每一条边可以选两个节点中的一个，问最多能选多少个节点）；如果连出来的是一个环，则答案即为 \(siz\)（每条边都可以选一个点）。
一个小优化是，我们发现答案即为 \(\min(cnt,siz)\)（虽然对于每条边都可以选一个没选过的点，但是如果有重边和自环呢），考虑用并查集维护。对于每个点到根的路径都要做一次询问，则我们用可持久化并查集维护即可。
12/23
-
考虑 \(O(n^2)\) 暴力，记录下所有的修改信息，查询时从头扫一遍，统计每个三角形加对矩形查询的贡献，分类讨论三角形相对于矩形的位置。
-
很容易想到离线下来，“插入+标记+回收”。考虑每次修改其实就是对 \(x\le \cfrac{a_i}{2}\) 的询问修改成 \(-x+a_i\)，用平衡树实现。维护两个 tag 标记：区间取反，区间加。注意可能 push_down 容易写错。
-
口胡一个不知道多少分的做法。考虑分块，首先容易 \(O(n)\) 预处理出对于 \(x\) 来说每个块内的最长合法长度，以及块初连续的一段最长合法长度，块末最长的一段连续合法长度。这样查询是 \(O(\sqrt{n})\) 的，单次修改也是 \(O(\sqrt{n})\) 的。空间复杂度 \(O(n\sqrt{n})\)，显然开不下，但是注意到数组中大部分位置都为空，可以用哈希表存，但可能常数会很大。
12/24
-
观察发现原题中的 \(d_i\) 其实就是第 \(i\) 个连通块的入度。要使图连通，其实就是求一颗生成树，考虑 Prufer 序列。先来回顾一下 Prufer 序列的结论：\(k\) 个连通块，第 \(i\) 个连通块大小为 \(s_i\)，加 \(k-1\) 条边使得图连通的方案数。考虑枚举 \(d\) 序列，对于入度 \(d_i\)，\(i\) 在 Prufer 序列中出现的次数为 \(d_i-1\)，则
\[\begin{aligned} \binom{k-2}{d_1-1,d_2-1\ldots d_k-1}=\cfrac{(k-2)!}{(d_1-1)!(d_2-1)!\ldots (d_k-1)!} \end{aligned}\]对于第 \(i\) 个连通块，他的连接方式有 \(s_i^{d_i}\) 种，因此对于给定 \(d\) 序列使得图连通的方案数为
\[\binom{k-2}{d_1-1,d_2-1\ldots d_k-1}\times \prod\limits_{i=1}^k s_i^{d_i} \]枚举 \(d\) 序列，则
\[\sum\limits_{d_i\ge 1,\sum d_i=2k-2}\binom{k-2}{d_1-1,d_2-1\ldots d_k-1}\prod\limits_{i=1}^k s_i^{d_i} \]有 多元二项式定理
\[(x_1+x_2\ldots x_m)^p=\sum\limits_{c_i\ge 0,\sum c_i=p} \binom{p}{c_1,c_2,\ldots c_m}\times \prod\limits_{i=1}^m x_i^{c_i} \]令 \(e_i=d_i-1\)，则
\[\begin{aligned} &\sum\limits_{e_i\ge 0,\sum e_i=k-2}\binom{k-2}{e_1,e_2\ldots e_k}\times \prod\limits_{i=1}^ks_i^{e_i+1}\\ =&(s_1+s_2,\ldots s_k)^{k-2}\times\prod\limits_{i=1}^k s_i=n^{k-2}\times\prod\limits_{i=1}^k s_i \end{aligned}\]回到这道题，我们需要在方案数后面乘上权值
\[\begin{aligned} &\sum\limits_{d}\binom{k-2}{d_1-1,d_2-1\ldots d_k-1}\prod\limits_{i=1}^k s_i^{d_i}\times\prod_{i=1}^k d_i!\\ =&\sum\limits_{d}\cfrac{(k-2)!}{(d_1-1)!(d_2-1)!\ldots (d_k-1)!}\prod\limits_{i=1}^ks_i^{d_i}\times\prod\limits_{i=1}^k d_i!\\ =&(k-2)!\times \sum\limits_{d}\prod\limits_{i=1}^k d_is_i^{d_i} \end{aligned} \]我们发现 \((k-2)!\) 这项的取值已经固定了，那么只需求出后面的值即可。
记 \(f_{i,j}\) 表示考虑到了第 \(i\) 个连通块，\(\sum d_i=j\) 时，上述式子后面的值，则
\[f_{i,j}=\sum\limits_{d=1}^{j-1}d\times s_i^df_{i-1,j-d} \]但是这个是 \(O(n^3)\) 方的，考虑怎么优化，我们把 \(f_{i,j}\) 拆一下：
\[\begin{aligned} f_{i,j-1}&=s_i\times f_{i-1,j-2}+2s_i^2\times f_{i-1,j-3}+3s_i^3\times f_{i-1,j-4}\ldots\\ f_{i,j}&=s_i\times f_{i-1,j-1}+2s_i^2\times f_{i-1,j-2}+3s_i^3\times f_{i-1,j-3}\ldots\\ f_{i,j+1}&=s_i\times f_{i-1,j}+2s_i^2\times f_{i-1,j-1}+3s_i^3\times f_{i-1,j-2}\ldots \end{aligned}\]\(f_{i,j-1}\) 两边同乘 \(s_i\)，把 \(f_{i,j+1}\) 乘上 \(\cfrac{1}{s_i}\)
\[\begin{aligned} s_if_{i,j-1}&=s_i^2\times f_{i-1,j-2}+2s_i^3\times f_{i-1,j-3}+3s_i^4\times f_{i-1,j-4}\ldots\\ f_{i,j}&=s_i\times f_{i-1,j-1}+2s_i^2\times f_{i-1,j-2}+3s_i^3\times f_{i-1,j-3}\ldots\\ \cfrac{1}{s_i}f_{i,j+1}&=1\times f_{i-1,j}+2s_i\times f_{i-1,j-1}+3s_i^2\times f_{i-1,j-2}\ldots \end{aligned}\]抵消之后得到
\[\begin{aligned}s_if_{i,j-1}+\cfrac{1}{s_i}f_{i,j+1}=2f_{i,j}+f_{i-1,j}\\ f_{i,j}=2s_if_{i,j-1}+s_if_{i-1,j-1}-s_i^2f_{i,j-2} \end{aligned}\]然后就可以 \(O(n^2)\) 递推了
-
根据题意，\(B\) 序列最优情况下肯定要是一个单调递增的序列，\(C\) 序列最优情况下则是一个单调递减的序列。两个序列在值域上的连线可能出现交叉，那我们就来枚举这个交叉点，设为 \(x\)。
先考虑在交叉点之后的情况，我们肯定是要以 \(x\) 为起点找一个 LIS 和一个 LDS。如果一个数既不在 LIS 的序列上，又不在 LDS 的序列上，则它一定可以放在 \(B\) 或 \(C\) 中而不影响对答案的贡献。
考虑在交叉点之前的情况，类似的我们肯定也是要找一个 LIS 和 LDS。但我们发现一个数如果既不在 LIS 的序列上，又不在 LDS 的序列上，它不管加进哪个序列都会破坏原本对答案的贡献。所以说此时我们没办法，只能贪心的把对于 \(x\) 之上的点加入 \(C\) 序列，对于 \(x\) 之下的点加入 \(B\) 序列。
实现细节：
-
考虑到求得的 LIS 和 LDS 的数会有重合，我们得钦定一条分界线，分讨 \(x\) 是加入 \(B\) 还是加入 \(C\) 的情况。
-
由于我们要求的是一个后缀的 LIS 和 LDS，不妨从后往前枚举。
-
统计前面答案的时候，采取的是 \(O(n)\) 递推的方式。
-
12/25
-
QOJ 8079. Range Periodicity Query
初始时 \(S\) 为空，有一些字符，如果是大写则在 \(S\) 后面加上它的小写字符，如果是小写则在 \(S\) 前面加上它。给你一个序列 \(P\)，每次询问给定 \(k,l,r\)，让你求最小的 \(pl,p_{l+1}\ldots p_r\) 使得它是 \(s_k\) 的一个周期
首先，我们知道如果 \(p\) 是 \(S\) 的一个周期，则 \(n-p\) 是 \(S\) 的一个 border。对于每一个字符串 \(s'\)，它能作为周期的一定是一段连续的区间。我们可以通过二分+哈希 \(O(n\log n)\) 对于每个字符串找出这个区间。
类似于函数复合时的“插入+标记+回收”的思想，我们同样的对于每个询问在 \(l\) 时插入平衡树，在 \(r+1\) 时回收。每次查询 \(s'\) 所管的区间，区间取 min 即可。
-
设 \(a_i\) 表示以 \(i\) 结尾有多少个 \(AA\)，\(b_i\) 表示以 \(i\) 开始有多少个 \(AA\)，则答案为：
\[\sum\limits_{i=1}^n a_i\times b_{i+1} \]怎么快速统计 \(a_i\) 和 \(b_i\) 呢？我们枚举 \(A\) 的长度 \(len\)，每 \(len\) 个位置放一个关键点，则串 \(AA\) 必过两个关键点。
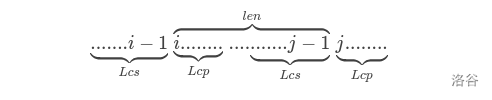
考虑一张如上的图，如果 \(lcp+lcs<len\) 的话，则一定不能构成 \(AA\) 串。否则，\(A\) 串终点落在中间两端 \(lcp,lcs\) 有交的部分都是合法的。
枚举 \(len\)，再枚举每一段，复杂度是调和级数 \(O(n\log n)\)。如果求 \(lcp,lcs\) 用哈希+二分实现，则还要再带一个 log，也可以用 SA+ST 表不带 log
-
题目其实就是让求循环同构的排名，我们直接把 \(S\) 复制一遍接在后面，转化为求后缀数组即可。
12/26
-
P2870 [USACO07DEC] Best Cow Line G
从字符串首尾取字符，求组成的字符串的字典序最小。按照贪心思路，肯定是比较当前的首字符和尾字符，谁小取谁。但是当首尾字符相等呢？比较后一位，这样的复杂度能被卡到 \(O(n^2)\)，但是也可以用哈希+二分带个 \(\log\)。这里我用了后缀数组，\(O(n)\) 去做这个事。发现每次比较其实就是考察一个正串的后缀和一个反串的后缀。我们把原串复制一遍后翻转接在后面，中间插入一个极小值，防止后面的被算入前面的贡献。然后就是裸的 SA 板子，每次比较首尾字符的 \(rk\) 即可。
-
这道题应该可以算是前缀线性基板子了。由于线性基只有 \(\log\) 个，所以可以在每个位置都存一组线性基。\(a_{i,j}\) 表示第 \(i\) 位的第 \(j\) 个线性基；\(pos_{i,j}\) 表示第 \(i\) 位的第 \(j\) 个线性基取到的位置。考虑位置 \(r\)，对于每次询问能对它做出贡献的一定是 \(pos_{r,j}\ge l\) 的。我们贪心的考虑 \(pos_{r,j}\) 一定是越大越好，每次在插入的时候考虑这个即可。
12/27
-
观察题目，比较显然的是后一个人的奖金一定比前一个人多，然后我们就可以直接列式子用邻项交换法，设 \(i<j\)，\(i\) 上一个人拿到的奖金为 \(W\)，\(\sum\limits_{j=1}^{i-1} a_j=S\)，则：
\[\begin{aligned} \max\Big(\max(W,P+a_i)+b_i,P+a_i+a_j\Big)+b_j&\le \max\Big(\max(W,P+a_j)+b_j,P+a_i+a_j\Big)+b_i\\ \max\Big\{W+b_i+b_j,P+a_i+b_i+b_j,P+a_i+a_j+b_j\Big\}&\le \max\Big\{W+b_j+b_i,P+a_j+b_j+b_i,P+a_i+a_j+b_i\Big\}\\ \max(a_i+b_i+b_j,a_i+a_j+b_j)&\le \max(a_j+b_j+b_i,a_j+a_i+b_i)\\ \max(b_i,a_j)+a_i+b_j&\le \max(b_j,a_i)+a_j+b_i\\ \max(b_i,a_j)-b_i-a_j&\le \max(b_j,a_i)-b_j-a_i\\ -\min(b_i,a_j)&\le -\min(b_j,a_i)\\ \min(b_j,a_i)&\le \min(b_i,a_j) \end{aligned}\] -
根据区间 DP 的套路，设 \(f_{i,j,k}\) 表示只考虑完全包换在 \([i,j]\) 之间的区间，区间最小值 \(\ge k\) 时贡献的最大值是多少，枚举一个特殊位置转移即可。这道题的特殊位置即为价格最小在哪取到的点，转移如下：
\[f_{i,j,k}=\max(f_{i,j,k+1},\max\{f_{i,p-1,k}+f_{p+1,k}+val\}) \]其中 \(val\) 表示在区间 \([i,j]\) 之内，跨过 \(p\) 点，且 \(c\ge k\) 的人的贡献，可以 \(O(mn^2)\) 预处理前缀和得到。离散化一下 \(c\) 数组，为了得到方案，我们还需记录每个点是由哪个最佳方案转移来的，递归得到答案即可。
-
注意他问的是全局的最大 border 为多少，我们不妨考虑枚举 border 的长度 len，看它能作为哪些修改的答案。
首先如果长度为 len 合法，则它肯定可以作为那些没有更新到这个区间和更不更新没变化的答案；否则，我们二分找到第一个不合法的位置，考虑分别在第一段和第二段改动这个位置，判断改动后是否合法，合法则更新答案。
-
首先对于一杯 \(r\) 相似的酒，它肯定也是 \(i(i\le r)\) 相似的。对于一杯 \(r\) 相似的酒，其实就是要求，\(h\) 数组中一段连续的区间 \(\ge r\)。考虑 \(r\) 单调递减时，区间范围只增不降，类似于合并两个区间。考虑用并查集维护，从后往前扫 \(r\)，合并区间，统计答案即可。
-
拆式子：
\[\begin{aligned} &\sum\limits_{1\le i<j\le n}\text{len}(T_i)+\text{len}(T_j)-2\times \text{lcp}(T_i,T_j)\\ &=(n-1)\times \cfrac{n(n+1)}{2}-2\times \sum\limits_{1\le i<j\le n} \text{lcp}(T_i,T_j) \end{aligned}\]把 lcp 转化为 h 数组连续的一段区间的最小值。把每个 lcp 的贡献都算在该最小值上，类似于启发式分裂即可。
-
考虑每一个子串都是一个后缀的前缀，转化题意，求 \(\sum\limits_{1\le i< j\le n} \text{lcp}(T_i,T_j)\) 的值，然后就可以类似上题用启发式分裂做，其实也可以用单调栈做，复杂度都是 \(O(n)\) 的。
