改题记录

https://imgse.com/album/bNZBF

https://blog.csdn.net/qq_45353993/article/details/129109027

记录一下欠的账吧

9/22

✘园艺 斜率优化dp，某人说我能改

9/23

✘光纤 听说能学到新东西，貌似是旋转凸壳？🤔🤔

9/24

✔ 三分 至少得会个板子吧🤔🤔

✔价值 貌似目前我解决地很困难😜😜

✘货币 好歹赛时写了这么久，还是把他改了吧，顺便学习网络流👍👍

9/27

记住两个式子：

$$C_n^x=C_n^{n-x}$$

and

$$C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$$

根据它们可以推导得到：在 $n$ 个数中选奇数个数的方案数等于

$$C_n^1+C_n^3+C_n^5...=2^{n-1}$$

✔字符串 “少改一半，集训两个月就损失了一个月”

考虑贪心，首先分析题目性质：

• 对于 $c$ 来说，就是规定了每次 $AB$ 切换获得“最大价值”的“最小代价”，例如：当 $c=3$ 时，每次的切换就形如：$BBBABBBA$ 这样切换，如果只考虑 $c$ 的贡献是最优的

• 对于 $a,b$ 来说，相当于把字母放成连续的一串，第一次产生贡献需要 $a+1$ 个字母 $A$，第二次产生贡献需要 $a$ 个字母 $A$，同样 $b$ 也一样

考虑枚举 $A$ 和 $B$ 切换了多少次，例如 $c=3$ 我们想 $BBBABBBA$ 这样切换，就能知道此时 $A$ 和 $B$ 各剩多少个，以及最后的结尾字符为 $A$。根据这些，我们可以贪心求该切换次数下的最大贡献（思考是否需要枚举是 $A$ 在前还是 $B$ 在前，答案是否，因为当 $A$ 在前的时候就相当于是 $B$ 在前的时候贪心，往前面加了一个 $A$）

• 先考虑把 $A$ 用完

  1. 如果此时 $A$ 还有剩余，我们可以直接在序列最前面（$B$ 前）加一个 $A$，这样花费了一个 $A$，拿到了 $1$ 的贡献
  2. 如果还有剩，就将多余的 $A$ 填充进序列里，由于每处的 $A$ 都为 $1$，就相当于每多 $a$ 个 $A$，就多 $1$ 的贡献

• 此时再考虑 $B$

  1. 如果序列的末尾是 $A$ 的话，我们可以再最后面加一个 $B$，这样花费了一个 $B$，拿到了 $1$ 的贡献
  2. 考虑用剩余的 $B$，先将序列中用于切换的 $B$ 补成 $b+1$ 个，剩下的 $B$ 就相当于，每多 $b$ 个 $B$，就多 $1$ 的贡献

✔奇怪的函数 听说可做，我应该能改？

感觉这题非常有意义啊，不仅启发了一些做题的性质，而且我觉得这题的代码还非常的巧妙。

• 考虑部分分
  1. 对于测试点 $1$，直接 $O(nq)$ 暴力即可做
  2. 对于测试点 $2\sim 6$ 分析题目，不容易的发现它是一个分段函数，如下图，我们对于每个操作，更新它们的端点值 $L$ 和 $R$，即可做到 $O(1)$ 查询
  $$f(x)=\{\begin{array}{ll}A& x<L\\ x+C& L\le x\le R\\ B& x>R\end{array}$$
  3. 对于测试点 $7\sim 11$，最多只有 $10$ 个 $max$ 和 $min$ 操作，直接用树状数组维护 $1$ 操作对应的区间内的和，对于每一次询问，分段计算即可，$O(10)$ ？
  4. 对于测试点 $12\sim 16$的部分分，$DDP$ 当然是不会的啦😒😒
• 考虑正解
  对于任意一段操作区间 $[L,R]$，它都是一个形如测试点 $2\sim 6$ 所说的分段函数，那么我们可以用线段树维护每段区间的分段函数，$O(\log n)$ 内完成一个操作的修改，$O(1)$ 回答询问。

我觉得代码里值得深思的东西有很多，Estelle_N 代码写的太好了

#include<bits/stdc++.h>
#define int long long
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
const int maxx=1e5+5;
const int maxn=3e5+5;
const int INF=1e9;
int read(){
	int x=0,f=1;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
	while (c>='0'&&c<='9') {x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return x*f;
}
int n,q,a[maxn],b[maxn];
struct Node{
	int l,r,o,v;
}f[10];
struct Segtree{
	int l,r,c;
	Node t[3];
}tr[maxn<<2];
void push_up(int rt){
	int k=-1;
	for (int i=0;i<tr[ls].c;i++)
		for (int j=0;j<tr[rs].c;j++)
			if (!tr[ls].t[i].o){//f(x) 一条直线 
				if (tr[ls].t[i].v>=tr[rs].t[j].l&&tr[ls].t[i].v<=tr[rs].t[j].r){
					if (tr[rs].t[j].o)//g(x) 一条斜线 
						f[++k]=Node{tr[ls].t[i].l,tr[ls].t[i].r,0,tr[ls].t[i].v+tr[rs].t[j].v};
					else//g(x) 一条直线 
						f[++k]=Node{tr[ls].t[i].l,tr[ls].t[i].r,0,tr[rs].t[j].v};
				}
			}
			else{//f(x) 一条斜线 
				int L=tr[ls].t[i].l+tr[ls].t[i].v;
				int R=tr[ls].t[i].r+tr[ls].t[i].v;
				if (L<=tr[rs].t[j].r&&R>=tr[rs].t[j].l){//有交集 
					L=max(L,tr[rs].t[j].l)-tr[ls].t[i].v;
					R=min(R,tr[rs].t[j].r)-tr[ls].t[i].v;
					if (tr[rs].t[j].o)
						f[++k]=Node{L,R,1,tr[ls].t[i].v+tr[rs].t[j].v};
					else 
						f[++k]=Node{L,R,0,tr[rs].t[j].v};
				}
			} 
	tr[rt].c=0;
	for (int i=0;i<=k;i++)//去重
		if (i!=0&&f[i-1].o==f[i].o&&f[i-1].v==f[i].v) 
			tr[rt].t[tr[rt].c-1].r=f[i].r;
		else tr[rt].t[tr[rt].c++]=f[i];
	tr[rt].t[0].l=0;tr[rt].t[tr[rt].c-1].r=INF;
}
void solve(int rt,int l){
	if (a[l]==1){
		tr[rt].c=1;
		tr[rt].t[0]=Node{0,INF,1,b[l]};//x+v
	}
	else if (a[l]==2){
		tr[rt].c=2;
		tr[rt].t[0]=Node{0,b[l],1,0};//x
		tr[rt].t[1]=Node{b[l],INF,0,b[l]};//A
	}
	else{
		tr[rt].c=2;
		tr[rt].t[0]=Node{0,b[l],0,b[l]};//B
		tr[rt].t[1]=Node{b[l],INF,1,0};//x
	}
}
void build(int rt,int l,int r){
	tr[rt].l=l;tr[rt].r=r;
	if (l==r) return solve(rt,l),void();
	int mid=(l+r)>>1;build(ls,l,mid);
	build(rs,mid+1,r);push_up(rt);
}
void update(int rt,int pos){
	if (tr[rt].l==tr[rt].r)
		return solve(rt,tr[rt].l),void();
	int mid=(tr[rt].l+tr[rt].r)>>1;
	if (pos<=mid) update(ls,pos);
	else update(rs,pos);
	push_up(rt);
}
void Work(int o,int pos,int v){
	o=read();
	if (o<=3){
		pos=read();v=read();
		a[pos]=o;b[pos]=v;
		update(1,pos);
	}
	else{
		v=read();
		for (int i=0;i<tr[1].c;i++)
			if (v>=tr[1].t[i].l&&v<=tr[1].t[i].r){
				if (tr[1].t[i].o) printf("%lld\n",v+tr[1].t[i].v);
				else printf("%lld\n",tr[1].t[i].v);
				break;
			}
	}
}
signed main(){
	freopen("function.in","r",stdin);
	freopen("function.out","w",stdout);
	n=read();
	for (int i=1;i<=n;i++)
		a[i]=read(),b[i]=read();
	build(1,1,n);q=read();
	while (q--) Work(0,0,0);
}

9/28

✔斯坦纳树 估计今天打了 ABC 后是改不完了

首先不难看出，点集在树上的斯坦纳树即为其虚树。虚树上的边权和即为其正确答案。

考虑题目的一个性质：设虚树上的点集为 $V{1}^{\prime }$，给定的点集为 $V1$，只有当 $V{1}^{\prime }=V1$ 时，答案才是正确的。

证：假设虚树上有虚点（即在 $V{1}^{\prime }$ 中不在 $V1$ 中）此时用该错误算法更新与改虚点直接相连的关键点，只能由其它关键点更新，而不能由该虚点更新，这样就多算了一段路径。

得出了这个性质，这道题就迎刃而解了。但是还有一些小细节：

1. 比如说怎么动态维护虚树上的点：开一个 $set$ 重载运算符为按 $dfn$ 序从小到大排列，每次往里面加一个点，取出它和它相邻点的 $lca$ 加入到 $set$ 中

2. 对于边权为 $0$ 的情况怎么看：把边权为 $0$ 的边所连接的点当做一个连通块，每次选中连通块中的一个点，即为选中该连通块，用并查集维护就好

3. 这道题的根节点并不一定是 $1$：如果都是 $1$ 的话，有些数据手模一下过不了，每次要把序列 $p$ 中的第一个点设为 $rt$

9/30

✔median 应该是签到题，签到题又没签上到

设序列编号为 $\text{{A,B,C,D,E}}$

考虑枚举每一个数为中位数的情况，此时就能确定该中位数的序列编号为多少，同时枚举它前面的另外两个序列编号为多少，这样就能确定它后面的连个序列编号了。

我们对于除了中位数序列的其它序列，考虑确定该位置能填多少数，设中位数的序列编号为 $u$，需要确定的序列编号为 $v$，中位数为 $k$，$v$ 中选出的数为 $x$：

• $v$ 中选出的数在中位数之前：

  1. $v<u$，此时要求 $x\le k$

  2. $v>u$，此时要求 $x<k$

• $v$ 中选出的数在中位数之后：

  1. $v<u$，此时要求 $x>k$

  2. $v>u$，此时要求 $x\ge k$

以上可以通过 $\text{lower\_bound}$ 和 $\text{upper\_bound}$ 轻易求出，注意在使用这两个函数的时候，一定要注意边界情况，特判当没有找到符合条件的值的时候的返回值！！！

✔travel 最重要的是读懂题

首先 $lim$ 的意思是极限，“有趣”的时候就是不存在极限，也叫它的函数图像“不皱缩”

题目就是求是否有一个点对 $(x,y)$ 的 $f$ 函数在 $k\to +\mathrm{\infty }$ 时形如下图：

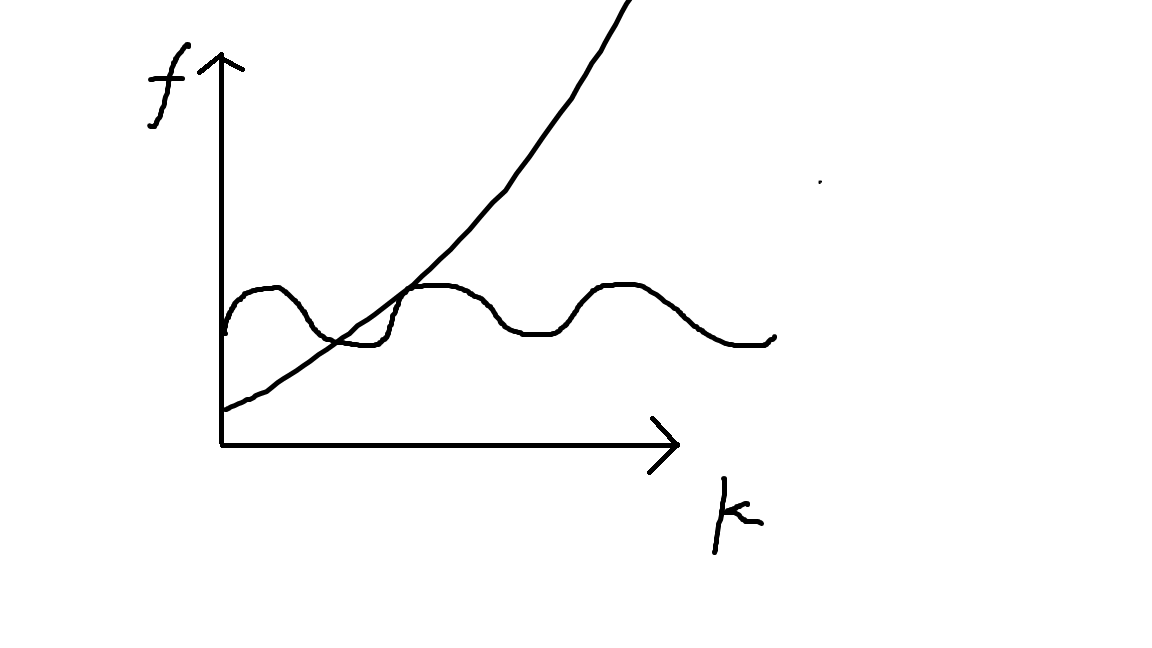
• 图中的波浪线可以看出是一个周期函数，考虑什么时候能有这样的周期：存在环，且环的大小不为 $1$（为 $1$ 的时候是一条直线）

• 考虑什么时候有图中的斜线：如果存在两个连通的自环，那么它就可以在第一个自环一直绕圈（想走多少走多少）假设走 $k1$ 次，从第一个自环到第二个自环经过的路程为 $p$，在第二个自环饶了 $k2$ 圈，只需要满足 $k1+p+k2=k$ 即可，所以你可以随意分配 $k1$ 和 $k2$ 的大小形成很多种方案，且随 $k$ 的增大而递增

代码中有一些小细节，判环可以用拓扑排序判，注意一个点上有两个自环也算在情况二内。

✔game 博弈论，不用 SG 函数

• 法一

  取自 Estelle_N，打表猜结论。结论为：所有数的出现次数都为偶数则先手必败，否则先手必胜。

  证明 ：

  1. 考虑只有两堆石子分别为 $1,1$ 的情况，此时肯定是先手必败的局面
  2. 考虑只有两堆石子分别为 $x,x(x>1)$ 的情况，无论先手怎么操作，后手都可以把局面变成另一个 $y,y$，直到 $y=1$ 此时先手必败
  3. 剩下的懒得证了

记录一个打表代码

#include<bits/stdc++.h>
#define se second
#define fi first
#define pb push_back
#define pp pop_back
using namespace std;
const int maxn=2e5+5;
int read(){
	int x=0,f=1;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
	while (c>='0'&&c<='9') {x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return x*f;
}
vector<int>x;
int T,n,sum,a[maxn];
map<vector<int>,bool>f;
bool find(vector<int> x);
bool dfs(vector<int> x,int pos,int k){
	if (!k){//石子分配完了 
		sort(x.begin(),x.end());
		return find(x);
	}
	//石子没分配完，但是已经分配了所有的石子堆 
	if (pos==(int)x.size()) return 1;
	for (int i=0;i<=k;i++){
		x[pos]+=i;
		if (!dfs(x,pos+1,k-i))
			return 0;
		x[pos]-=i;
	}
	return 1;
}
bool find(vector<int> x){
	//记忆化 
	if (f.count(x)) return f[x];
	else sum=0;
	for (auto it:x) sum+=it;
	//边界条件 
	if (!sum) return 0;
	if (x.size()==1) return 1;
	vector<int>y;
	for (int i=0;i<(int)x.size();i++)//枚举对 i 进行操作 
		for (int j=1;j<=x[i];j++){//枚举拿走了 j 个石子 
			y.clear();//不分配
			for (int k=0;k<(int)x.size();k++) 
				if (k!=i) y.pb(x[k]);
			if (x[i]-j)
				y.push_back(x[i]-j);
			sort(y.begin(),y.end());
			if (!find(y)) return f[x]=1;
			if (x[i]==j) continue;
			y.clear();//分配
			for (int k=0;k<(int)x.size();k++)
				if (k!=i) y.pb(x[k]);
			for (int k=1;k<=x[i]-j;k++){//枚举分配了 k 个石子 
				if (x[i]-j-k) y.pb(x[i]-j-k);
				if (!dfs(y,0,k)) return f[x]=1;
				if (x[i]-j-k) y.pp();
			} 
		}
	return f[x]=0;
}
void Work(){
	n=read();x.clear();
	for (int i=1;i<=n;i++)
		a[i]=read();
	sort(a+1,a+n+1);
	for (int i=1;i<=n;i++)
		x.push_back(a[i]);
	printf("%s\n",find(x)?"Yes":"No");
}
signed main(){
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	T=read();while (T--) Work();return 0;
}

最后记录一个博弈论的定理：

1. 一个必胜状态的后继状态至少有一个为必败状态

2. 一个必败状态的后继状态都为必胜状态

✔counter 很清奇的做法，感觉改完后，码力++

首先需要读出，这道题是让你求 $x$ 到 $y$ 的最短路：对任意一个 $k$，对 $k$ 和它能到达的点连一条有向边，边权为 $1$，跑最短路

注意到我们每次最多移动 9 个点，所以从一段区间的左半部分移动到右半部分肯定会经过中间$9$ 个点的至少一个，故考虑分治，我觉得我可能一辈子都联想不到分治

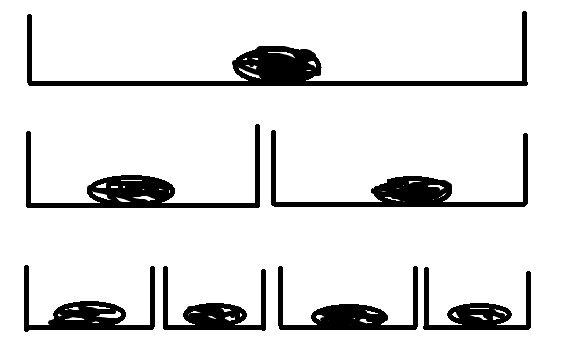
每段区间中的黑圈为中间点，我们预处理出区间 $(l,r)$ 到区间中每个中间点的距离以及中间点到其它的距离，由于边权为 $1$，所以 $dijkustra$ 的复杂度为 $O(n)$，一共 $\log n$ 层，所以总复杂度为 $O(9\times n\log n)$

查询，当 $(x,y)$ 的区间与中间点的区间有交集时（即跨越了中间点），直接用之前预处理的答案更新就好；否则，继续递归查询

小技巧：

1. 处理正向距离（中间点到其它点）的时候，由 $k$ 向它所能到达的点连边，此时跑出来的就是中间点到其它点的距离；在处理反向距离（其它点到中间点）的时候，可以反向建边，此时跑出来的最短路即为其它点到中间点的距离

2. 在存区间 $(l,r)$ 中的点到中间点的距离的时候，设 $f_{d,i,id,0/1}$ 表示当前是在第 $d$ 层，由 $i$ 到第 $id$ 个中间点的反向/正向距离

记录改题的一次胜利

#include<bits/stdc++.h> 
using namespace std;
const int N=20;
const int maxn=1e5+105;
const int INF=1e9;
int read(){
	int x=0,f=1;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
	while (c>='0'&&c<='9') {x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return x*f;
}
bool vis[maxn];
int f[N][maxn][10][2];
int T,las,dis[maxn],tag[maxn];
vector<int>e[maxn];
void dij(int s){
	queue<int>q;
	dis[s]=0;q.push(s);
	while (q.size()){
		int x=q.front();q.pop();
		if (vis[x]) continue;
		vis[x]=1;
		for (auto to:e[x])
			if (!vis[to]&&dis[to]>dis[x]+1)
				dis[to]=dis[x]+1,q.push(to);
	}
}
void caldis(int d,int l,int r,int s,int id){
	for (int i=1;i<=9;i++) tag[i]=0;
	int L=max(l-30,0),R=r+30;
	for (int i=L;i<=R;i++){
		int x=i;e[i].clear();
		dis[i]=INF;vis[i]=0;
		while (x){
			if (x%10&&tag[x%10]!=i){
				int u=x%10;tag[u]=i;
				if (i+u<=R) e[i].push_back(i+u);
				if (i-u>=L) e[i].push_back(i-u);
			}	
			x/=10;
		}
	}
	dij(s);
	for (int i=l;i<=r;i++)
		f[d][i][id][1]=dis[i];//me to other
	for (int i=1;i<=9;i++) tag[i]=0;
	for (int i=L;i<=R;i++) e[i].clear();
	for (int i=L;i<=R;i++){
		int x=i;dis[i]=INF;vis[i]=0;
		while (x){
			if (x%10&&tag[x%10]!=i){
				int u=x%10;tag[u]=i;
				if (i+u<=R) e[i+u].push_back(i);
				if (i-u>=L) e[i-u].push_back(i);
			}
			x/=10;
		}
	}
	dij(s);
	for (int i=l;i<=r;i++)
		f[d][i][id][0]=dis[i];//other to me
}
void build(int d,int l,int r){
	if (r-l+1<=9){
		for (int i=l;i<=r;i++)
			caldis(d,l,r,i,i-l);
		return ;
	}
	int mid=(l+r)>>1,L=mid-4,R=mid+4;
	for (int i=L;i<=R;i++)
		caldis(d,l,r,i,i-L);
	if (l<L) build(d+1,l,L-1);
	if (r>R) build(d+1,R+1,r);
}
int query(int d,int l,int r,int x,int y,int o){
	if (r-l+1<=9){
		int ans=INF;
		for (int i=l;i<=r;i++)	
			ans=min(f[d][x][i-l][o]+f[d][y][i-l][!o],ans);
		return ans==INF?-1:ans;
	}
	int mid=(l+r)>>1,L=mid-4,R=mid+4;
	if (x<=R&&y>=L){
		int ans=INF;
		for (int i=L;i<=R;i++){
			ans=min(f[d][x][i-L][o]+f[d][y][i-L][!o],ans);
		}
		return ans==INF?-1:ans;
	}
	if (y<L) return query(d+1,l,L-1,x,y,o);
	else return query(d+1,R+1,r,x,y,o);
}
void Work(){
	int x=read(),y=read(),o;
	x^=(las+1);y^=(las+1);o=0;
	if (x>y) swap(x,y),o^=1;
	if (x==y) las=0;
	else las=query(0,0,1e5+30,x,y,o);
	printf("%d\n",las);
}
signed main(){
	freopen("counter.in","r",stdin);
	freopen("counter.out","w",stdout);
	memset(f,0x3f,sizeof(f));
	T=read();
	build(0,0,1e5+30);
	while (T--) Work();return 0;
}

10/1

✔score and rank 思路清奇，甚至看了题解后都有点不明白为什么

题意简述：删掉序列中的若干个数，使得任意一个区间的和 $<S$，最小化删掉元素的个数

容易得出当 $S<=0$，直接把所有 $a_i\ge S$ 的数删掉即可（剩下的数都为负数，只会越加越小）

那么就只需考虑 $S>0$ 的情况：

• 如果 $a_i$ 都是正数，我们从前往后加数，用一个 $\text{multiset}$ 维护当前序列中的最大后缀，如果最大后缀的 $sum\ge S$，就弹出此时 $\text{multiset}$ 中的最大值（能证明最后得到的序列中任意区间的 $sum<S$，而且删掉的数最少）

• 如果 $a_i$ 中有负数：

  1. 当前最大后缀的 $sum+a_i\le 0$ 直接清空 $\text{mulitset}$（因为在 $a_i$ 后的任意一段区间跨越 $a_i$ 后都会减小，所以不用考虑）

  2. 否则一定能找到某几个较小的数，使得它们相加恰好 $\ge a_i$，我们用这些较小数抵消 $a_i$ 的影响，使 $a_i$ 为正，然后再加入 $a_i$（看代码就懂了）

代码真的又少又清晰

#include<bits/stdc++.h>
#define int long long
#define in insert
#define er erase
#define cl clear
using namespace std;
const int maxn=1e6+5;
int read(int x=0,bool f=1,char c=0){
	while (!isdigit(c=getchar())) f=c^45;
	while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return f?x:-x;
}
multiset<int>s;
int n,m,ans;
int sum,a[maxn];
signed main(){
	freopen("score.in","r",stdin);
	freopen("score.out","w",stdout);
	n=read();m=read();
	if (m<=0){
		for (int i=1;i<=n;i++)
			ans+=read()>=m;
		return printf("%lld\n",ans),0;
	}
	for (int i=1,x;i<=n;i++){
		x=read();
		if (x>0){
			sum+=x,s.in(x);
			if (sum>=m){
				auto it=prev(s.end());
				sum-=*it;s.er(it);++ans;
			}
		}
		else if (x<0){
			if (sum+x<=0) sum=0,s.cl();
			else{
				sum+=x;
				while (x<0){
					auto it=s.begin();
					x+=*it;s.erase(it);
				}
				s.insert(x);
			}
		}
	}
	return printf("%lld\n",ans),0;
}

✔HZOI大作战 主要是倍增的状态设计

$u$ 到 $v$ 一共要换的板子数可以分解成很多个 $2$ 次幂相加，由此设 $g_{i,j}$ 表示由 $i$ 开始换 $2^j$ 次板子达到的点。

怎么求解 $g$ 数组，设 $va{l}_{i,j}$ 表示从 $i$ 往上跳 $2^j$ 步所经过的路径上不包括 $f_{i,j}$ 的“码风优秀度” $a_i$ 的最大值，转移为：

for (int i=1,u=i;i<=n;i++){
    for (int j=log2(d[i]);j>=0;j--)
        if (val[u][j]<=a[i]) u=f[u][j];
    g[i][0]=u;u=i+1;
}

话不多说，看代码

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int maxn=5e5+5;
int read(int x=0,bool f=1,char c=0){
	while (!isdigit(c=getchar())) f=c^45;
	while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return f?x:-x;
}
vector<int>he[maxn];
int ans=1,val[maxn][21];
int n,q,a[maxn],d[maxn];
int f[maxn][21],g[maxn][21];
void dfs(int x,int fa){
	d[x]=d[fa]+1;f[x][0]=fa;
	val[x][0]=a[x];
	for (auto to:he[x])
		if (to!=fa) dfs(to,x);
}
void init(){
	for (int j=1;j<=log2(n);j++)
		for (int i=1;i<=n;i++){
			f[i][j]=f[f[i][j-1]][j-1];
			val[i][j]=max(val[i][j-1],val[f[i][j-1]][j-1]);
		}
	for (int i=1;i<=n;i++){
		int to=i;
		for (int j=log2(d[i]);j>=0;j--)
			if (val[to][j]<=a[i])
				to=f[to][j];
		g[i][0]=to;
	}
	for (int j=1;j<=log2(n);j++)
		for (int i=1;i<=n;i++)
			g[i][j]=g[g[i][j-1]][j-1];
}
signed main(){
	freopen("accepted.in","r",stdin);
	freopen("accepted.out","w",stdout);
	n=read();q=read();
	for (int i=1;i<=n;i++)
		a[i]=read();
	for (int i=1,x,y;i<n;i++){
		x=read();y=read();
		he[x].pb(y);he[y].pb(x);
	}
	dfs(1,0);init();
	for (int i=1,u,v,c;i<=q;ans=1,i++){
		u=read();v=read();c=read();
		for (int j=log2(d[u]);j>=0;j--)
			if (val[u][j]<=c) u=f[u][j];
		if (d[u]<d[v]){printf("0\n");continue;}
		if (d[u]==d[v]){printf("1\n");continue;}
		for (int j=log2(d[u]);j>=0;j--)
			if (d[g[u][j]]>=d[v])
				ans+=(1<<j),u=g[u][j];
		printf("%d\n",ans);
	}
}

✘Delov的旅行

✘gtm和joke的星球

10/3

✔构造字符串 就是没最后连边，挂了 30 分

对于相同的位置用并查集维护，看成一个点

对于不相同的位置连边，每次贪心的从小到大枚举 $i$ 填数，$an{s}_i$ 即为与它相连的边中 $an{s}_j$ 的 $\text{mex}$

补：$\text{mex}$ 的定义为最小的没有出现过的自然数

注意在维护并查集的时候应该把编号大的父亲设为编号小的，同时在连边时，应先把操作离线下来，最后再连

✔寻宝 啊啊啊，这么简单的题，我赛时的时候干嘛去了

我们把所有相连的“.”看成一个连通块，用并查集维护，传送门即为在这些连通块之间连边，跑一遍弗洛伊德看是否连通就好。

注意弗洛伊德的复杂度为 $O(n^3)$，连通块的个数可以达到 $5\times {10}^4$，直接跑肯定会 T，注意到 $k$ 就是边数 $\le 100$，我们可以把有连边的点放进一个集合里，对它跑弗洛伊德，不在集合里的直接不用管它。特判一下在同一个连通块的情况即可

✔序列 趁这个机会学习了一下李超线段树

首先我们可以发现对于答案的区间 $(l,r)$ 其实可以拆成两段计算，即为 $(l,p_i)$ 和 $(p_i+1,r)$ 不影响结果，我并没发现

那我们现在就只需要讨论一种情况就好了，设 $a$ 的前缀和为 $sa$，$b$ 的前缀和为 $sb$

$$\begin{array}{rl}{f}_{l,p}& =\sum _{i=l}^p{a}_i-k\times \sum _{i=l}^p{b}_i\\ & =s{a}_p-s{a}_{l-1}-k\times (s{b}_p-s{b}_{l-1})\\ & =s{a}_p-k\times s{b}_p-(s{a}_{l-1}-k\times s{b}_{l-1})\end{array}$$

前面的已知，我们只需求后面括号中的最小值，就变成了李超树的板子题，直接套就好

✘构树

10/4

✔挤压 我一直弄不清的期望。。。

对于一个异或和 $s$，定义它的二进制表示为 $(s_0{s}_1{s}_2...s_i)$，则

$$\begin{array}{rl}{s}^2& =(s_0\times 2^0+s_1\times 2^1+s_2\times 2^2...s_i\times 2^i{)}^2\\ & =\sum _{i,j\in (0,30)}{s}_i\times s_j\times 2^{i+j}\end{array}$$

考虑对于每一位分别计算 $s_i\times s_j\times 2^{i+j}$ 的期望。

看做把 $a_x$ 的第 $i,j$ 位拿出来写成一个两位的二进制数 $k$，可以理解成选择一些 $0\le k\le 3$ 的 $a_x$ 使得异或后的 $k$ 为 $3$

$k=0$ 的选项选与不选与答案都没关系，直接不考虑。现在只有两种情况：选了奇数个 $1$ 和 $2$，以及偶数个 $3$；选了偶数个 $1$ 和 $2$，以及奇数个 $3$

那么剩下的问题就是求对于每个 $k$ 选了奇数/偶数个的概率，设 $f_{i,0/1}$ 表示考虑了前 $i$ 个数，选了偶数/奇数个的概率，转移时考虑 $a_i$ 选与不选，初始化 $f_{0,0}=1,f_{0,1}=0$，转移如下：

if (check(a[i])){//表示可以转移
    f[i][0]=f[i-1][1]*p[i]+f[i-1][0]*(1-p[i]+mod)%mod;
    f[i][1]=f[i-1][0]*p[i]+f[i-1][1]*(1-p[i]+mod)%mod;
}

考虑 $i=j$ 时，直接计算第 $i$ 位为 $1$ 的概率，其实就是 $f[n][1]$

✔工地难题 只会打 20 分暴力

开局首先记住两个公式：

• $n$ 个数划分成 $m$ 个段（不可为空），方案数为 $C(n-1,m-1)$（隔板法）

• $n$ 个数划分成 $m$ 个段（可为空），方案数为 $C(n+m-1,m-1)$

正解：

最长连续段恰好为 $k$ 的时候难以处理，我们考虑对答案做一个前缀和，计算最长连续段不超过 $k$ 的方案数，答案即为 $an{s}_k-an{s}_{k-1}$

考虑我们用这些 $0$ 把 $1$ 分成了（$0$ 的个数 + $1$ 段）这些段可能为空。设 $1$ 的个数为 $n$，$0$ 的个数为 $m$，不考虑 $k$ 的限制，则此时答案即为 $C(n+m+1-1,m+1-1)$

这时我们再来考虑 $k$ 的影响，我们钦定有 $x$ 个段一定大于 $k$，怎么做呢？先从 $n$ 中把 $x\times (k+1)$ 个数拿走，再用 $0$ 把剩余的 $1$ 分成 $m+1$ 段，从这 $m+1$ 段中选出 $x$ 段，往其中加入 $k+1$ 就能保证有 $x$ 个段一定大于 $k$ 了。那答案不就用总方案数减去至少有 $1$ 个段大于 $k$ 的方案数不就好了？（后者即为 $C(n-x\times (k+1)+m+1-1，m+1-1)\times C(m+1,x)$）

最后一步容斥，思考为什么会减重复了，假设 $x=1$，现在有两个段，我们每次是固定其中一个段 $>k$，但是不能确保另一个段 $\le k$。当我们固定一号 $>k$ 时，二号也可能 $>k$；当我们固定二号 $>k$ 时，一号也可能 $>k$；此时我们把这用一种情况算了两次，所以需要容斥。

用总方案数 $-$ 至少一段大于 $k$ $+$ 至少两段大于 $k$ $-$ 至少三段大于 $k$....

$40$ 分暴力：

设 $f_{i,j,o}$ 表示考虑了前 $i$ 个数，填了 $j$ 个 $1$，结尾有 $o$ 个连续的 $1$ 的方案数，转移如下：

for (int k=1,las=0;k<=m;k++){
    int ans=0;f[0][0][0]=1;
    for (int i=1;i<=n;i++)
        for (int j=0;j<=min(i,m);j++)
            for (int o=0;o<=min(j,k);o++){
                if (i-j&&i-j<=m) f[i][j][0]+=f[i-1][j][o];
                if (o) f[i][j][o]+=f[i-1][j-1][o-1];
             }
      for (int i=0;i<=k;i++)
          ans+=f[n][m][i];
      printf("%lld ",ans-las);
      las=ans;
}

此时算出来的 $ans$ 为最长连续段不超过 $k$ 的方案数，而我们要求的是恰好为 $k$ 的方案数，就用 $ans$ 减去最长连续段不超过 $k-1$ 的方案数即可（$las$）。空间开不下，注意到转移只与 $i-1$ 有关，可以滚动数组压一维。

✔星空遗迹 关键是要想到维护单调栈

$60$ 分：

可以发现当一段字符为“强弱强”时，比如 $RSR$，只考虑这一段答案只会为 $R$；当一段字符串全重复时，比如 $RRR$，只考虑这一段答案只会是 $R$。同理，开头和结尾符合“弱强”/“强弱”的比如 $SSSR$ 的也可以直接删去

结论：我们可以维护一个单调递减的栈，栈顶为 $top$，即将加进来的字符为 $a_i$，考虑加进来的 $a_i=top$ 此时可以直接跳过，不把 $a_i$ 加进来；$a_i>top$ 此时 $a_i$ 一定等于 $top-1$ 符合“强弱强” 直接把 $top$ 和 $a_i$ 都删掉。此时我们就会了 $O(n)$ 的查询方法，可以拿到 $60$ 分

正解：

对于每一段区间 $(l,r)$ 其实就是要求它最后一次栈底的元素，设 $f_i$ 为考虑前 $i$ 位数后，栈的大小。即为求 $(l,r)$ 中最后一次 $f_i=1$ 时候的元素值

考虑 $f_i$ 的转移情况：

$$f_i=\{\begin{array}{ll}{f}_{i-1}+1& s_i<s_{i-1}\vee i=1\\ f_{i-1}& s_i=s_{i-1}\\ max(f_{i-1}-1,1)& x_i>s_{i-1}\end{array}$$

这个和 $1$ 取 $max$ 不是很好处理，可以直接把取 $max$ 去掉，最后一个 $f_i=1$ 的位置就是去掉 $max$ 后的 $f_i$ 有最小值的位置。

把 $f_i$ 的转移看成一个前缀和的转移，这样就可以把单点修改变成：区间修改，区间查询。每次讨论 $a_x$（要修改的点）与 $a_{x-1}$ 和 $a_{x+1}$ 的情况，记得在更改前要清空未修改时 $a_x$ 与 $a_{x-1}$ 和 $a_{x+1}$ 的贡献

✘纽带 题读不懂，暴力也不会打。。。

鉴于正解超出能力范围，故只写暴力。

首先如果你知道一个小函数 next_permutation(a+1,a+n+1) 生成给定序列的下一个字典序排列，它将会减少点你的代码量

其次，对于 $l,l+1,l+2\dots r$ 的排列，取最小值一定为 $l$，取最大值一定为 $r$。同理，如果不是上面序列的排列，取最大值和最小值，总有一个不等于 $l$/$r$

还有，别去枚举 $k$ 了，对于一个排列 $p$ 它的 $k$ 值肯定是固定的，我真傻，真的

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=15;
const int maxn=105;
const int INF=1e18;
int read(int x=0,bool f=1,char c=0){
	while (!isdigit(c=getchar())) f=c^45;
	while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return f?x:-x;
}
int n,m[N];
int p[N],ans[maxn];
signed main(){
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	n=read();
	for (int i=1;i<=n;i++)
		p[i]=i,m[i]=read();
	do{
		bool flag=1;int cnt=0;
		for (int l=1;l<=n;l++){
			for (int r=l,mi=p[l],ma=p[l];r<=m[l];r++){
				mi=min(mi,p[r]);ma=max(ma,p[r]);
				if (mi==l&&ma==r){flag=0;break;}
			}
			if (!flag) break;
		}
		if (!flag)continue;
		for (int l=1;l<=n;l++)
			for (int r=l,mi=p[l],ma=p[l];r<=n;r++){
				mi=min(mi,p[r]);ma=max(ma,p[r]);
				if (mi==l&&ma==r) ++cnt;
				if (mi<l) break;
			}
		ans[cnt]++;
	}
	while (next_permutation(p+1,p+n+1));
	for (int i=1;i<=n*(n+1)/2;i++)
		printf("%lld ",ans[i]);
} 

10/11

✔好数（number） 签到题签上到了耶

考虑 $n^2$ 做法:

$a_i$ 为好数即为存在 $a_i=x+y+z$（$x,y,z$ 可以相等）。枚举 $x$，判断前面的数中是否存在两个数的和为 $a_i-x$ 即可。判断是否存在首先想到的是用 $\text{set}$ 维护，但是带个 $\log$ 本地跑极限数据跑到了 $2.6$ 秒。后来发现 $a_i$ 的数据范围很小，可以直接开 $vis$ 数组维护，数据有负数，设一个偏移变量即可。

✔SOS字符串（sos） 赛时一眼简单题，发现思路假了破大防，后来一眼没看

考虑 DP 做法：

设 $f_{i,j,0/1/2}$ 表示考虑了前 $i$ 个字符，已经匹配上了 $j$ 个 $SOS$ 串，当前匹配到了 $SOS$ 中的第 $0/1/2$ 个字符，复杂度 $O(n^2)$，转移也挺好写的，期望得分 $40$ 分。

怎么优化，接下来就是今天的重头戏 “正难则反”，考虑当 $j>=3$ 的时候都对答案有贡献，我们可以只算出 $j<3$ 的答案设为 $k$，用总方案数减去 $k$ 即可，复杂度 $O(n)$。

✔集训营的气球（balloon） 写了个线段树维护 DP 的做法，结果发现正解在它下面

• 直接考虑 DP，设 $f_{i,j}$ 表示考虑了前 $i$ 个字符，有 $j$ 个人选了一血气球，转移方程即为 $f_{i,j}=f_{i-1,j}\times b_i+f_{i-1,j-1}\times a_i[j>0]$，实际上我们可以在枚举 $j$ 的时候倒着转移，空间上优化掉一维，也方便实现后面的正解，复杂度 $O(n^{2}q)$。

• 又又考虑到 “正难则反”，发现 $c$ 很小，则我们可以用总方案数减去 $j$ 小于 $c$ 的方案数，现在复杂度就变成了 $O(nqc)$，期望得分 $30$ 分。

• 我们发现这题实际上是一个动态 $dp$ 的问题，考虑用线段树维护，由于空间过大开不下，采用动态开点，相当于 $n$ 个叶子节点，总点数最多为 $2\times n$，期望得分 $80$ 分。加一道动态 DP 的扩展 [ABC246Ex] 01? Queries 用到了矩阵加速和线段树维护

• 正解做法为退背包，参考 P4141 消失之物 。我们空间优化后的转移方程式为 $f_j=f_j\times b_i+f_{j-1}\times a_i$，正着背包是逆序枚举 $j$，所以退包应为正序枚举 $j$。把转移方程移项得，原本的 $f_j=\frac{f_j-f_{j-1}\times a_i}{b_i}$。一定要记得 $f_0$ 的更新，和它的更新顺序，退包与背包的更新顺序是反着的。复杂度 $O(nc+qc)$，期望得分 $100$ 分。

线段树代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=21;
const int maxn=2e6+1;
const int mod=1e9+7;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int cnt=1,n,c,q,a[maxn],b[maxn];
struct Segtree{
    int l,r,tot;
    int f[N],ls,rs;
}tr[maxn];
void push_up(int rt){
    for (int i=0;i<c;i++)
        tr[rt].f[i]=0;
    for (int i=0;i<c;i++)
        for (int j=0;i+j<c;j++)
            tr[rt].f[i+j]=(tr[rt].f[i+j]+(ll)tr[tr[rt].ls].f[i]*tr[tr[rt].rs].f[j]%mod)%mod;
    tr[rt].tot=(ll)tr[tr[rt].ls].tot*tr[tr[rt].rs].tot%mod;
}
void build(int rt,int l,int r){
    tr[rt].l=l;tr[rt].r=r;
    if (l==r){
        tr[rt].f[0]=b[l];
        tr[rt].f[1]=a[l];
        tr[rt].tot=a[l]+b[l];
        return void();
    }
    tr[rt].ls=++cnt;tr[rt].rs=++cnt;
    int mid=(l+r)>>1;build(tr[rt].ls,l,mid);
    build(tr[rt].rs,mid+1,r);push_up(rt);
}
void update(int rt,int pos){
    if (tr[rt].l==tr[rt].r){
        tr[rt].f[0]=b[tr[rt].l];
        tr[rt].f[1]=a[tr[rt].l];
        tr[rt].tot=a[tr[rt].l]+b[tr[rt].l];
        return void();
    }
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (pos<=mid) update(tr[rt].ls,pos);
    else update(tr[rt].rs,pos);push_up(rt);
}
signed main(){
    freopen("balloon.in","r",stdin);
    freopen("balloon.out","w",stdout);
    n=read();c=read();
    for (int i=1;i<=n;i++)
        a[i]=read();
    for (int i=1;i<=n;i++)
        b[i]=read();
    q=read();build(1,1,n);
    for (int i=1,o,x,y;i<=q;i++){
        o=read();x=read();y=read();
        a[o]=x;b[o]=y;update(1,o);
        int sum=tr[1].tot,ans=0;
        for (int j=0;j<c;j++)
            ans=(ans+tr[1].f[j])%mod;
        printf("%d\n",(sum-ans+mod)%mod);
    }
}

退包

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=21;
const int maxn=1e6+1;
const int mod=1e9+7;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int tot,n,c,q,a[maxn],b[maxn];
int f[N],fac[maxn],inv[maxn],ifa[maxn];
void init(){
    tot=f[0]=1;
    for (int i=1;i<=n;i++){
        for (int j=c-1;j>0;j--)
            f[j]=(f[j]*b[i]%mod+f[j-1]*a[i]%mod)%mod;
        f[0]=f[0]*b[i]%mod;tot=tot*(a[i]+b[i])%mod;
    }
}
int qpow(int a,int b){
    int res=1;
    while (b){
        if (b&1) res=res*a%mod;
        a=a*a%mod;b>>=1;
    }
    return res;
}
signed main(){
    freopen("balloon.in","r",stdin);
    freopen("balloon.out","w",stdout);
    n=read();c=read();
    for (int i=1;i<=n;i++)
        a[i]=read();
    for (int i=1;i<=n;i++)
        b[i]=read();
    q=read();init();
    for (int i=1,o,x,y;i<=q;i++){
        o=read();x=read();y=read();
        //-> back
        tot=tot*qpow(a[o]+b[o],mod-2)%mod;
        int t=qpow(b[o],mod-2);f[0]=f[0]*t%mod;
        for (int j=1;j<c;j++)
            f[j]=(f[j]-f[j-1]*a[o]%mod+mod)*t%mod;
        //-> go
        a[o]=x;b[o]=y;int ans=0;
        for (int j=c-1;j>0;j--)
            f[j]=(f[j]*b[o]%mod+f[j-1]*a[o]%mod)%mod,ans=(ans+f[j])%mod;
        tot=tot*(x+y)%mod;f[0]=f[0]*y%mod;;
        printf("%lld\n",(tot-ans-f[0]+2*mod)%mod);
    }
}

✘连通子树与树的重心（tree） 赛时看半天没看懂样例是怎么得出来的，就弃了

P4582 [FJOI2014] 树的重心 貌似是上面那题的弱化版

P2680 [NOIP2015 提高组] 运输计划 图论没做完的题

10/12

✔小 Z 的手套（gloves） 我居然也会在赛时写二分了

签到题没什么好说的，“最大值最小” 一眼二分，数据范围 $O(n\log n)$ 是足够的，甚至可以 $O(n\log n\log n)$ 接下来是思考怎么 $O(n\log n)$ $\text{check}$ 答案的合法性。分别将左手套和右手套按尺码排序，每次遍历左手套，对于第 $i$ 个手套它能匹配的右手套一定是一个区间，每次贪心地让它和该区间的的左端点匹配上（给后面的手套留下更多的可操作空间）。不能匹配时，则该 $mid$ 非法，返回 $0$。

多带一个 $\log$ 貌似会被卡，我加了一个小优化，每次 $\text{check}$ 时里面的 $\text{lowerbound}$ 在 $\text{las}+1$ 到 $n$ 里查找，$\text{las}$ 为 $i-1$ 匹配到的位置。

code

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int n,m,L[maxn],R[maxn];
bool check(int x){
    int las=1;
    for (int i=1;i<=n;i++){
        if (las>m) return 0;
        int t=lower_bound(R+las,R+m+1,L[i]-x)-R;
        if (t>m) return 0;
        if (R[t]>L[i]+x) return 0;
        las=t+1;
    }
    return 1;
}
int binary_search(int l,int r){
    while (l<r){
        int mid=(l+r)>>1;
        if (check(mid)) r=mid;
        else l=mid+1;
    }
    return l;
}
signed main(){
    freopen("gloves.in","r",stdin);
    freopen("gloves.out","w",stdout);
    n=read();m=read();
    for (int i=1;i<=n;i++)
        L[i]=read();
    for (int i=1;i<=m;i++)
        R[i]=read();
    sort(L+1,L+n+1);
    sort(R+1,R+m+1);
    if (n>m){
        for (int i=1;i<=m;i++)
            swap(L[i],R[i]);
        for (int i=m+1;i<=n;i++)
            R[i]=L[i],L[i]=0;
        swap(n,m);
    }
    int MAX=max(L[n]-R[1],R[n]-L[1]);
    printf("%d\n",binary_search(0,MAX));
}

✔小 Z 的字符串（string） 贪了半天啥也没贪出来，还挂了20分

赛时尝试想了想 DP，设 $f_{i,0/1/2}$ 表示考虑了前 $i$ 个，当前结尾为 $0/1/2$ 的最小操作步骤，结果发现 DP 信息太少，写不出转移方程式，遂罢，愣是一点没想到 $400$ 的数据范围怎么可能是 $O(n)$ 的！！！你也不知道多设点东西，那信息不就来了吗？？？而且当时想了半天怎么由结尾为 $0$ 转移到结尾为 $0$，TMD 就不能转移，结论是我是 SB

正解：设 $f_{i,j,k,l,0/1/2}$ 表示考虑了前 $i$ 个，用了 $j$ 个 $0$，$k$ 个 $1$，$l$ 个 $2$，且最后结尾为 $0/1/2$ 的方案数，转移挺好写的，以 $f_{i,j,k,l,0}$ 为例：

if (j>0) f[i][j][k][l][0]=min(f[i][j-1][k][l][1],f[i][j-1][k][l][2])+abs(pos-i);

其中 $pos$ 为第 $j$ 个 $0$ 在原序列的位置，为什么呢？“首先有一个比较显然的性质，即相同数字的相对位置不会改变。” 不知道是它并不显然，还是我赛时的时候显然是个**，反正我赛时的时候是一点没想到。所以对于 $pos$ 就等于第 $j$ 个 $0$ 所在的位置，对于每一种数字记录一下就好了。注意这种写发最后取得是绝对值，最终的答案要除以 $2$

还有一种写法是不用除以 $2$ 的，可以理解为如果 $pos<i$ 的话，那在你把前面的数排好时，你的这个 $0$ 就已经被挤到当前的 $i$ 位置了，代码如下：

if (j>0) f[i][j][k][l][0]=min(f[i][j-1][k][l][1],f[i][j-1][k][l][2])+max(0,pos-i);

此时的转移明显是 $O(n^4)$，肯定过不了。有一个明显的优化就是把 $f_{i,j,k,l,0/1/2}$ 优化为 $f_{i,j,k,0/1/2}$，因为此时的 $l=i-j-k$。行，我们照着这个写了，...$0$ 分？？？全 RE 了，算一下空间居然开不下，所以此时我们需要考虑另一个优化，$f_{i,j,k,0/1/2}$ 表示有 $i$ 个 $0$，$j$ 个 $1$，$k$ 个 $2$，所以当前考虑到了 $i+j+k$ 的位置，复杂度 $O(n^3)$，期望得分 $100$ 分

赛时为什么挂了 $20$ 分呢？原来是返回值忘写了，真正的 CSP 和 NOIP 可千万别忘了，如下：

if (check()) return printf("-1");

其实应该是。。。。

if (check()) return printf("-1"),0;

code

#include<bits/stdc++.h>
using namespace std;
const int maxx=405;
const int maxn=205;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
char s[maxx];
int cnt0,cnt1,cnt2;
int n,a[maxx],r[3][maxx];
int f[maxn][maxn][maxn][3];
bool check(){
    if (cnt0>(n+1)/2) return 1;
    if (cnt1>(n+1)/2) return 1;
    if (cnt2>(n+1)/2) return 1;
    return 0;
}
signed main(){
    freopen("string.in","r",stdin);
    freopen("string.out","w",stdout);
    scanf("%s",s+1);
    n=strlen(s+1);
    for (int i=1;i<=n;i++){
        a[i]=s[i]-'0';
        if (a[i]==0) r[0][++cnt0]=i;
        if (a[i]==1) r[1][++cnt1]=i;
        if (a[i]==2) r[2][++cnt2]=i;
    }
    if (check()) return printf("-1\n"),0;
    memset(f,0x3f,sizeof(f));
    f[0][0][0][0]=f[0][0][0][1]=f[0][0][0][2]=0;
    for (int i=0;i<=cnt0;i++)
        for (int j=0;j<=cnt1;j++)
            for (int k=0;k<=cnt2;k++){
                int p=i+j+k;
                if (i) f[i][j][k][0]=min(f[i][j][k][0],min(f[i-1][j][k][1],f[i-1][j][k][2])+max(0,r[0][i]-p));
                if (j) f[i][j][k][1]=min(f[i][j][k][1],min(f[i][j-1][k][0],f[i][j-1][k][2])+max(0,r[1][j]-p));
                if (k) f[i][j][k][2]=min(f[i][j][k][2],min(f[i][j][k-1][1],f[i][j][k-1][0])+max(0,r[2][k]-p));
            }
    printf("%d\n",min({f[cnt0][cnt1][cnt2][0],f[cnt0][cnt1][cnt2][1],f[cnt0][cnt1][cnt2][2]}));
}

✔一个真实的故事（truth） 第一次模拟赛场切两道，虽然是由于数据太水？？

赛时由于 $T2$ 想了太久，就首先写了一个 $O(nm)$ 的暴力，由于剩下的时间不多了怕又耽误太久，就先去把 $T4$ 的暴力写了。回过头来写了一个带线段树的暴力，复杂度虽然也是 $O(nm)$，但是在随机数据下跑的比正解还快,但是赛后被卡了。

错解：

对于每一个 $i$ 位置，记录上一次 $x(x\in 1,2,3\dots k)$ 出现的位置为 $a_{i,x}$，以 $i$ 结尾的合法序列的长度 $le{n}_i=i-min(a_{i,x})+1$，最终的 $ans=min(le{n}_i)$。用线段树维护 $le{n}_i$ 的最小值，支持单点修改和区间查询。

对于每一个询问 $q$，设修改前的值为 $x$，修改后的值为 $y$，修改的位置为 $pos$，从 $pos$ 往后遇到的第一个为$x$ 的位置为 $posx$，遇到的第一个为 $y$ 的位置为 $posy$。我们把 $a_{i,x}(i\in [pos,posx])$ 的值更新为 $a_{pos-1,x}$，把 $a_{i,y}(i\in [pos,posy])$ 更新为 $pos$，在遍历的同时在线段树上更新 $le{n}_i$，维护全局答案即可。

code

#include<bits/stdc++.h>
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
const int maxn=5e4+5;
const int INF=1e9;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int a[maxn][35];
int n,m,k,b[maxn];
int c[35],ans=INF;
struct Segtree{
    int l,r,val;
}tr[maxn<<2];
void build(int rt,int l,int r){
    tr[rt].l=l;tr[rt].r=r;
    tr[rt].val=INF;
    if (l==r) return ;
    int mid=(l+r)>>1;
    build(ls,l,mid);
    build(rs,mid+1,r);
}
void update(int rt,int pos,int val){
    if (tr[rt].l==tr[rt].r)
        return tr[rt].val=val,void();
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (pos<=mid) update(ls,pos,val);
    else update(rs,pos,val);
    tr[rt].val=min(tr[ls].val,tr[rs].val);
}
signed main(){
    freopen("truth.in","r",stdin);
    freopen("truth.out","w",stdout);
    n=read();k=read();
    m=read();build(1,1,n);
    for (int i=1;i<=k;i++) 
        a[0][i]=c[i]=-INF;
    for (int i=1;i<=n;i++){
        b[i]=read();c[b[i]]=i;
        int mi=INF;
        for (int j=1;j<=k;j++)
            a[i][j]=c[j],mi=min(mi,c[j]);
        update(1,i,i-mi+1);
    }
    for (int i=1,op,p,x,y;i<=m;i++){
        op=read();
        if (op==2) printf("%d\n",tr[1].val>5e4?-1:tr[1].val);
        else {
            p=read();x=read();y=b[p];
            if (x==y) continue;
            bool flagx=0,flagy=0;
            for (int j=p;j<=n;j++){
                if (flagx&&flagy) break;
                if (j!=p&&!flagy&&b[j]==y) flagy=1;
                if (!flagx&&b[j]==x) flagx=1;
                if (!flagy) a[j][y]=a[p-1][y];
                if (!flagx) a[j][x]=p;
                int mi=INF;
                for (int o=1;o<=k;o++)
                    mi=min(mi,a[j][o]);
                update(1,j,j-mi+1);
            }
            b[p]=x;
        }
    }
}

正解：

同样是用线段树维护答案，对于线段树上的每个点记录最右的 $1\sim k$ 出现的位置，以及最左的 $1\sim k$ 出现的位置，同时记录 $(l,r)$ 中的一个答案。

考虑是否可以合并，我们发现合并时更新前两个很好更新，关键时怎么更新 $ans$。有一个很明显的性质，新的 $ans$ 只可能是 $ls$ 的 $ans$，与 $rs$ 的 $ans$，以及中间过渡部分的 $ans$ 中的一个。

思考怎么计算中间过渡部分的 $ans$，其实 $O(k^2)$ 很好实现，但是过不去 $\text{hack}$ 数据。当左右两个块需要合并时，取出左块最右的 $1\sim k$ 和右块最左的 $1\sim k$，按出现位置 sort 后用双指针可以 $O(k\log k)$ 实现。

code

#include<bits/stdc++.h>
#define pai pair<int,int>
#define fi first
#define se second
#define mk make_pair
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
const int maxn=5e4+5;
const int INF=1e9;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int n,k,m,a[maxn];
struct Segtree{
    int l,r,ans,rc[31],lc[31];
}tr[maxn<<2];
void push_up(int rt){
    int res=INF,sum=0,vis[k+1]={0};
    int cnt=0;pai t[2*k+1];
    for (int i=1;i<=k;i++){
        if (tr[ls].lc[i]) tr[rt].lc[i]=tr[ls].lc[i];
        else tr[rt].lc[i]=tr[rs].lc[i];
        if (tr[rs].rc[i]) tr[rt].rc[i]=tr[rs].rc[i];
        else tr[rt].rc[i]=tr[ls].rc[i];
        if (tr[ls].rc[i]) t[++cnt]=mk(tr[ls].rc[i],i);
        if (tr[rs].lc[i]) t[++cnt]=mk(tr[rs].lc[i],i);
    }
    for (int i=1;i<=k;i++)
        if (!tr[rt].lc[i])
            return tr[rt].ans=INF,void();
    sort(t+1,t+cnt+1,[](pai x,pai y){
        return x.fi<y.fi;});
    for (int i=1,j=1;i<=cnt;i++){
        if (t[i].fi==0) continue;
        while (j<=cnt&&sum<k){
            if (t[j].fi!=0){
                if (!vis[t[j].se]) sum++;
                vis[t[j].se]++;
            }j++;
        }
        if (sum==k) res=min(res,t[j-1].fi-t[i].fi+1);
        if (--vis[t[i].se]==0) sum--;
    }
    tr[rt].ans=min({res,tr[ls].ans,tr[rs].ans});
}
void build(int rt,int l,int r){
    tr[rt].l=l;tr[rt].r=r;
    tr[rt].ans=INF;
    if (l==r){
        tr[rt].rc[a[l]]=l;
        tr[rt].lc[a[l]]=l;
        return void();
    }
    int mid=(l+r)>>1;build(ls,l,mid);
    build(rs,mid+1,r);push_up(rt);
}
void update(int rt,int pos,int val){
    if (tr[rt].l==tr[rt].r){
        tr[rt].rc[val]=tr[rt].l;
        tr[rt].lc[val]=tr[rt].l;
        tr[rt].rc[a[tr[rt].l]]=0;
        tr[rt].lc[a[tr[rt].l]]=0;
        return void();
    }
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (pos<=mid) update(ls,pos,val);
    else update(rs,pos,val);push_up(rt);
}
signed main(){
    freopen("truth.in","r",stdin);
    freopen("truth.out","w",stdout);
    n=read();k=read();m=read();
    for (int i=1;i<=n;i++)
        a[i]=read();
    build(1,1,n);
    for (int i=1,o,p,v;i<=m;i++){
        o=read();
        if (o==2) printf("%d\n",tr[1].ans>5e4?-1:tr[1].ans);
        else {
            p=read();v=read();
            if (v==a[p]) continue;
            update(1,p,v);a[p]=v;
        }
    }
}

✘异或区间（xor） 怎么还得学笛卡尔树啊，不想学

衍生出来的一些东西 关于异或的区间问题 以及 RMQ问题

10/17

✔传送 (teleport) 哎，签到题没签上 😦

首先一眼看到 $min(|x_i-x_j|,|y_i-y_j|)$ 这个式子，昨天才推了，但是这里显然不是。我们发现它相当于是一个完全图再加了一些重边，然后思路就卡这儿一动不动了。其实之前也遇到过类似于完全图求最短路径，最小贡献的题。知道要排序，但是这道题我还是没想到怎么做。

其实还是没有理解这类题为什么要排序的本质，一般都是因为排序后和相邻点的贡献是最优的。怎么理解这道题排序后和相邻点连边？考虑前面部分分的做法，排序后的点权就相当于放在了一条数轴上，传送就相当与是在数轴上走了一段连续的距离。设当前要从 $x$ 走到 $y$，首先你肯定走的是 $x$ 到 $y$ 的直线距离，这条直线距离不能由 $x$ 到 $y$ 连边（因为这样是 $O(n^2)$ 的），但是可以拆分成很多条短的直线线段 $x$ 到 $x+1$，$x+1$ 到 $x+2$，$\dots$ 到 $y$。所以对于部分分做法，我们直接在相邻点之间连边即可。

那想拿到满分怎么办呢？其实还是一样的，分别把 $x$ 和 $y$ 都排序，再连接相邻点。思考这么做为什么是对的，$x$ 和 $y$ 的切换，可以看做在两条数轴上分别走了一段。此时还需要考虑取 $min$ 操作吗？不需要了，因为你跑最短路时取得肯定是最小值啊。

✔排列 (permutation) 一眼感觉很可做，然后发现读假了

我再说一遍，当你想 DP 的时候，发现转移写不出来，一定要多设几维！！！能不能别转不出来硬转啊，你就不能多设几维吗？数据范围摆在那儿，你设个 $O(n)$ 的 DP 是个什么意思？？？

正解：设 $f_{i,j,k}$ 表示已经填了前 $i$ 位数，关键点的出现情况为 $j$（二进制状压），最后一个点填的是 $k$。只有 $10$ 位数字是关键的，那就可以考虑把其它无意义点全看做 $1$，最后在乘上它们的方案数即可。DP 最重要的就是设状态，设好状态后就很好转移了。时间复杂度 $O(n\times 2^{10}\times {11}^2)$，如果不用滚动数组的话，就不能开 long long，不然会爆空间。

✔战场模拟器 (simulator) 狂写线段树，本来以为能捞个 $50$ 的，但是挡不住它狂 T

赛后线段树调了半天，觉得自己写的相当没问题，可它就是 WA，发现我TM线段树空间开成了 maxn<<1。。。

对于第一档部分分，直接暴力就好，得分 $9$ 分。

对于第二档部分分，考虑用线段树维护，由于它保证了不会死亡，对于每个点记录区间的最小值，以及最小值的个数。查询时当区间最小值等于 $0$ 时，返回最小值的个数，否则返回 $0$。得分 $32$ 分。

对于第三档部分分，发现每次只是对一个人加护盾，最多只有 $Q$ 个护盾。我们用 $\text{set}$ 维护一下哪些点有护盾，暴力撤销区间减对它的影响即可。均摊复杂度 $O((N+Q)\log N)$，得分 $51$ 分。

部分分代码

#include<bits/stdc++.h>
#define int long long 
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
const int maxn=2e5+5;
const int INF=1e18;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int n,a[maxn],Q,pro[maxn];
struct Query{
    int o,l,r,x;
}q[maxn];
void solve1(){
    for (int i=1,o,l,x;i<=Q;i++){
        o=q[i].o;l=q[i].l;x=q[i].x;
        if (o==1){
            if (pro[l]) pro[l]--;
            else{
                a[l]-=x;
                if (a[l]<0) a[l]=-INF;
            }
        }
        else if (o==2) a[l]+=x;
        else if (o==3) pro[x]++;
        else if (o==4) printf(a[l]<0?"1\n":"0\n");
        else printf(a[l]==0?"1\n":"0\n");
    }
}
struct Segtree{
    int l,r,val,tag,tot;
}tr[maxn<<2];
void push_up(int rt){
    tr[rt].tot=0;
    tr[rt].val=min(tr[ls].val,tr[rs].val);
    if (tr[rt].val==tr[ls].val)
        tr[rt].tot+=tr[ls].tot;
    if (tr[rt].val==tr[rs].val)
        tr[rt].tot+=tr[rs].tot;
}
void upd(int rt,int k){
    tr[rt].tag+=k;tr[rt].val+=k;
}
void push_down(int rt){
    if (!tr[rt].tag) return ;
    int t=tr[rt].tag;tr[rt].tag=0;
    return upd(ls,t),upd(rs,t),void();
}
void build(int rt,int l,int r){
    tr[rt].l=l;tr[rt].r=r;
    if (l==r){
        tr[rt].val=a[l];
        tr[rt].tot=1;
        return void();
    }
    int mid=(l+r)>>1;build(ls,l,mid);
    build(rs,mid+1,r);push_up(rt);
}
void update(int rt,int l,int r,int k){
    if (tr[rt].l>=l&&tr[rt].r<=r)
        return upd(rt,k),void();
    push_down(rt);
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (l<=mid) update(ls,l,r,k);
    if (mid<r) update(rs,l,r,k);
    push_up(rt);
}
int query(int rt,int l,int r){
    if (tr[rt].l>=l&&tr[rt].r<=r){
        if (!tr[rt].val) return tr[rt].tot;
        return 0;
    }
    if (tr[rt].val>0) return 0;
    push_down(rt);int res=0;
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (l<=mid) res+=query(ls,l,r);
    if (mid<r) res+=query(rs,l,r);
    return res;
}
int stk[maxn],top;
set<int>s;
void solve2(){
    build(1,1,n);
    for (int i=1,o,l,r,x;i<=Q;i++){
        o=q[i].o;l=q[i].l;r=q[i].r;x=q[i].x;
        if (o==1){
            update(1,l,r,-x);
            auto it=s.lower_bound(l);
            while (it!=s.end()&&*it<=r){
                update(1,*it,*it,x);
                pro[*it]--;
                if (!pro[*it]) stk[++top]=*it;
                it=next(it);
            }
            while (top) s.erase(stk[top--]);
        }
        else if (o==2) update(1,l,r,x);
        else if (o==3) {pro[x]++;s.insert(x);}
        else if (o==4) printf("0\n");
        else printf("%lld\n",query(1,l,r));
    }
}
signed main(){
    freopen("simulator.in","r",stdin);
    freopen("simulator.out","w",stdout);
    n=read();
    for (int i=1;i<=n;i++)
        a[i]=read();
    Q=read();bool flag=1;
    for (int i=1,o,l,r,x;i<=Q;i++){
        o=read();
        if (o<3){
            l=read();r=read();x=read();
            if (l!=r) flag=0;
            q[i]=Query({o,l,r,x});
        }
        else if (o==3){
            x=read();q[i]=Query({o,0,0,x});
        }
        else{
            l=read();r=read();
            if (l!=r) flag=0;
            q[i]=Query({o,l,r,0});
        }
    }
    if (flag) return solve1(),0;
    else return solve2(),0;
}

第四档部分分，线段树维护区间最小值，区间最小值的个数，区间已经死亡的人数。由于每个人只会死一次，因此当区间最小值小于这次的伤害值，就暴力到叶子更新就行，均摊复杂度 $O((N+Q)\log N)$。

满分做法，综合上述，线段树维护区间最小值，最小值个数，区间死亡人数，区间护甲个数。每次遇到护甲和死亡的情况直接暴力到叶子节点更新即可，均摊复杂度 $O((N+Q)\log N)$

code

#include<bits/stdc++.h>
#define int long long 
#define ls rt<<1
#define rs rt<<1|1
#define _4781 0
using namespace std;
const int maxn=2e5+5;
const int INF=1e18;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
int n,a[maxn],Q;
struct Segtree{
    int l,r,val,tag;
    int pro,tot,die;
}tr[maxn<<2];
void push_up(int rt){
    tr[rt].tot=0;
    tr[rt].die=tr[ls].die+tr[rs].die;
    tr[rt].pro=tr[ls].pro+tr[rs].pro;
    tr[rt].val=min(tr[ls].val,tr[rs].val);
    if (tr[rt].val==tr[ls].val)
        tr[rt].tot+=tr[ls].tot;
    if (tr[rt].val==tr[rs].val)
        tr[rt].tot+=tr[rs].tot;
}
void upd(int rt,int k){
    tr[rt].tag+=k;tr[rt].val+=k;
}
void push_down(int rt){
    if (!tr[rt].tag) return ;
    int t=tr[rt].tag;tr[rt].tag=0;
    return upd(ls,t),upd(rs,t),void();
}
void build(int rt,int l,int r){
    tr[rt].l=l;tr[rt].r=r;
    if (l==r){
        tr[rt].val=a[l];
        tr[rt].tot=1;
        return void();
    }
    int mid=(l+r)>>1;build(ls,l,mid);
    build(rs,mid+1,r);push_up(rt);
}
void del(int rt,int l,int r,int k){
    if (tr[rt].l>=l&&tr[rt].r<=r){
        if (tr[rt].pro){
            if (tr[rt].l==tr[rt].r)
                return tr[rt].pro--,void();
            push_down(rt);del(ls,l,r,k);
            del(rs,l,r,k);push_up(rt);
            return void();
        }
        if (tr[rt].val<k){
            if (tr[rt].l==tr[rt].r){
                tr[rt].val=INF;
                tr[rt].die=1;
                return void();
            }
            push_down(rt);del(ls,l,r,k);
            del(rs,l,r,k);push_up(rt);
            return void();
        }
        return upd(rt,-k),void();
    }
    push_down(rt);
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (l<=mid) del(ls,l,r,k);
    if (mid<r) del(rs,l,r,k);
    push_up(rt);
}
void add(int rt,int l,int r,int k){
    if (tr[rt].l>=l&&tr[rt].r<=r)
        return upd(rt,k),void();
    push_down(rt);
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (l<=mid) add(ls,l,r,k);
    if (mid<r) add(rs,l,r,k);
    push_up(rt);
}
int dead(int rt,int l,int r){
    if (tr[rt].l>=l&&tr[rt].r<=r)
        return tr[rt].die;
    push_down(rt);int res=0;
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (l<=mid) res+=dead(ls,l,r);
    if (mid<r) res+=dead(rs,l,r);
    return res;
}
void pro(int rt,int pos,int k){
    if (tr[rt].l==tr[rt].r)
        return tr[rt].pro+=k,void();
    push_down(rt);
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (pos<=mid) pro(ls,pos,k);
    else pro(rs,pos,k);
    push_up(rt);
}
int danger(int rt,int l,int r){
    if (tr[rt].l>=l&&tr[rt].r<=r){
        if (!tr[rt].val) return tr[rt].tot;
        return 0;
    }
    if (tr[rt].val>0) return 0;
    push_down(rt);int res=0;
    int mid=(tr[rt].l+tr[rt].r)>>1;
    if (l<=mid) res+=danger(ls,l,r);
    if (mid<r) res+=danger(rs,l,r);
    return res;
}
signed main(){
    freopen("simulator.in","r",stdin);
    freopen("simulator.out","w",stdout);
    n=read();
    for (int i=1;i<=n;i++)
        a[i]=read();
    Q=read();build(1,1,n);
    for (int i=1,o,l,r,x;i<=Q;i++){
        o=read();
        if (o==1) l=read(),r=read(),x=read(),del(1,l,r,x);
        else if (o==2) l=read(),r=read(),x=read(),add(1,l,r,x);
        else if (o==3) x=read(),pro(1,x,1);
        else if (o==4) l=read(),r=read(),printf("%lld\n",dead(1,l,r));
        else l=read(),r=read(),printf("%lld\n",danger(1,l,r));
    }
    return _4781;
}

✘ 点亮 (light) 发现自己连暴力分都不会打时就弃了

10/19

✔排列最小生成树 (pmst) 赛时以为 T1 是签，想不出来破防了

第一个转化，思考对于 $1$，最坏情况下的最优连边的边权是多少。答案是 $n$（其实应该是 $n-1$），例如 $1,2$ 与 $n,1$。所以对于一个点来说，只有当它连的边是 $\le n$ 的时候，才有可能被加入到最小生成树中。

第二个转化，我们怎么找到边权为 $\le n$ 的所有边。考虑只有当 $|i-j|\le \sqrt{n}$ 或 $|p_i-p_j|\le \sqrt{n}$ 的时候 $|i-j|\times |p_i-p_j|$ 才有可能 $\le n$。所以我们直接排序后 $O(n\sqrt{n})$ 枚举建边即可。

第三个转化，排序和是 $O(n\sqrt{n}\log n)$ 的怎么办？考虑值域范围很小啊（$n\le 5\times 4$），我们直接开一个桶来维护，这样就省去了排序。为了优化复杂度，我们用按秩合并来维护并查集。时间复杂度大概是 $O(n\sqrt{n}\alpha (n))$ 的。

✔卡牌游戏 (cardgame) 策略很差+心态不好，没看出来是签

首先对于前几档部分分，很容易看出当 $gcd(N,M)=1$ 的时候，对于每一个 $a_i(1\le i\le N)$，他在 $b$ 中会匹配上每一个 $b_j(1\le j\le M)$。直接对 $b$ 排个序后，每次二分统计答案即可。

考虑当 $gcd(N,M)\ne 1$ 的时候怎么做。另 $g=gcd(N,M)$，可以把它看做进行了 $g$ 轮，每轮匹配了 $\text{lcm}$ 个。容易看出对于每一轮，匹配情况都是一样的，那我们就只考虑其中一轮的情况，最后乘上一个 $g$ 就好了。其实通过手摸，真的特别特别容易看出来（你直接把每一轮每个 $i$ 匹配到的 $j$ 列出来，直接就看出来了我都不知道我赛时连手摸样例都没直接打暴力是怎么想的）规律就是每个 $i$ 匹配的下标其实就是 $j\equiv i(\mathrm{mod}g)$。所以现在就直接拿 $\text{vector}$ 来对于 $0\sim g-1$ 存一下就可以了

考虑怎么证这个结论啊，对于每一轮 $i$ 与 $j$ 会匹配上当且仅当 $(i+k_{1}n-1)\mathrm{mod}m+1=j$ 其中 $k_1$ 表示一共匹配了几个 $n$。我们移个项：

$$(i+k_{1}n-1)\mathrm{mod}m=j-1$$

$$(i+k_{1}n-1)=k_{2}m+j-1$$

$$k_{1}n-k_{2}m=j-i$$

我们发现整数 $k_1,k_2$ 使得上式成立的时候 $i$ 和 $j$ 能匹配上。由裴蜀定理可得，此时 $j-i=gcd(n,m)$，进一步推导可得 $i\equiv j(\mathrm{mod}g)$

✔比特跳跃 (jump) 连暴力分也挂了，特殊性质也没想其实通过大样例应该是看的出来的

• $S=1$

  按位与 &

  这一部分应该是最好想的：对于二进制结尾为 $0$ 的点，直接由 $1$ 跳，贡献为 $0$；否则，可以先由 $1$ 跳到任意一个结尾为 $0$ 其它位相同的点，再跳到该节点，此时贡献也为 $0$。

  但是有一个特例，例如 $n$ 的二进制表示为 $11111$ 的这种特殊情况，找不到合法的结尾为 $0$ 的节点给它跳。此时可以直接 $1\sim n-1$ 与 $n$ 建边，跑最短路即可。

• $S=2$

  按位异或 ^

  每一次异或产生的贡献主要由有多少个不同的 $1$ 决定。按位异或有一个性质啊，例如 $101010$ 可以由 $000010\to 101010$ 也可以由 $000010\to 001010\to 101010$ 这两种情况的贡献都是一样的。即多个不同的 $1$ 的情况可以由 $1$ 个不同的 $1$ 分次抵达。

  那我们就可以只考虑只有一个不同的 $1$ 的情况：对于每一个数枚举二进制下的每一位，如果该位为 $1$ 就向该位为 $0$ 且其它为相同的数连边（保证只有一个不同的 $1$，例如 $101$ 可以向 $001$ 和 $100$ 连边）。最后跑一个最短路即可，复杂度 $O(n\log n)$

• $S=3$

  按位或 |

  还是看性质吧：对于或操作来说，贡献与原来的 $x,y$ 相比肯定只增不减，所以 $x,y(x>y)$ 连边肯定不如 $1,y$ 连边；什么时候 $1$ 不如 $x$ 优呢？当 $x$ 是 $y$ 的子集的时候，$1$ 可能不如 $x$ 优。

  做法如下：由于我们不可能对于每个 $i$ 去枚举 $i$ 的子集，所以先由 $1$ 向 $2\sim n$ 连边，跑一遍最短路。在用 DP 去更新 $di{s}_i$，具体地，设 $f_i=min\left\{di{s}_j\right\}$ 其中 $j$ 是 $i$ 的子集，对于每个 $i$，枚举它只有一位不一样的子集更新即可。

✘区间 (interval) 区间历史版本和线段树，学学学！！！

10/29

✔追逐游戏 (chase) 赛时就知道这是签到题，但是赛时就知道自己没签上...

我也不知道赛时怎么就想了一个超级无敌巨多细节的分讨，而我甚至都不知道某些情况该怎么写判断条件，就这样我赛时硬磕了 $2$ 个小时，发现大样例过不去后摆烂了，只拿了 $35$ 分。赛后我真的是不撞南墙不回头，非要把那 shift 一样的代码调处来，又拿着硬调了一个半小时。后来发现自己真的不会写判断条件，改了一下分讨的情况，大概用了半个小时终于过了，跑的还特慢。最后花了 $3$ 分钟看了眼正解，用了 $5$ 分钟把正解打出来了，我.......

我跑的很慢的写法：$S$ 和 $S^{\prime }$ 一直跳，直到 $S^{\prime }$ 跳到 $S$ 到 $T$ 所在的路径上，复杂度可能是 $O(n{\log }^{2}n)$

正解：发现其实就只有两种情况，一是 $S^{\prime }$ 要比 $S$ 后到 $T$ 点，此时答案即为 $S^{\prime }$ 到 $T$ 的距离和 $T$ 点；二是 $S^{\prime }$ 要比 $S$ 先到 $T$ 点，此时 $S^{\prime }$ 一定可以在中间的某个地方转身实现和 $S$ 的双向奔赴，这段路程其实就相当于 $S$ 到 $S^{\prime }$ 的距离，最终到达哪个点也很好找，复杂度 $O(n\log n)$

✔统计 感觉自己每次都想不到用哈希解决问题

我们对于 $1\sim m-1$ 随一个哈希值作为它们的权值记为 $va{l}_i$，令 $va{l}_m=-\sum _{i=1}^{m-1}va{l}_i$

考虑当一段区间 $(l,r)$ 为合法时，这段区间出现的所有数的权值和为 $0$，即为 $\sum _{i=l}^{r}va{l}_{a_i}=0$

设 $s_i=\sum _{j=1}^{i}va{l}_{a_i}$，一段区间合法就可以转化为 $s_l-s_r=0$，即为 $s_l=s_r$

这样我们处理出 $s$ 数组后，将它们排个序，相邻两个两两比较即可。

✔软件工程 也是骗上暴力分了耶

感觉最近老是忘了写贪心这个东西，可能是被真正的贪心题老是贪假弄怕了。但是什么思路都没有的时候，写写贪心还是挺好的。

1. 把所有线段按长度从小到大排序，前 $k-1$ 条线段直接分别塞到 $1\sim k-1$ 个桶里，剩下的所有线段全塞到第 $k$ 个桶里。

2. 枚举 $i$，对于每个 $i$，贪心找到放在哪个桶里对贡献的增加量更多，就直接把它放进去，复杂度 $O(nk)$

这两种情况具体是怎么分出来的我还不是很清楚，咕。

✘命运的X 也是读不懂题了耶

10/31

✔四舍五入 签到题没签上，硬控 $1$ 小时

我们先考虑对于每个 $i$，它能被哪些数统计，打表发现这些区间都很零散，不易在一个较小的时间复杂度内统计。

正难则反，考虑对于每个 $j$，它能统计哪些数，发现其实合法的 $i$ 满足 $i\mathrm{mod}j>\frac{j+1}{2}$，（赛时想到这儿就没想了，去看 T2 了）。在转换一下就是 $i=kj+r,r<\frac{j+1}{2}$，这样我们就可以对于每个 $j$，枚举 $j$ 的倍数，用差分数组统计答案，时间复杂度是 $O(n\ln n)$

✔填算符 DP 写完了才发现这玩意儿根本不能用 DP

赛时硬控一小时读错题了，赛后又读错题了，直到讲题的时候才发现。

首先题目有一个结论：把所有的“与”运算符放在前 $k$ 个位置一定是最优答案的一种（考虑如果填“与”，则后一个数是它的上界；如果填“或”，则后一个数是它的下界）愣是没发现

然后我们就有了一种 $O(n^2)$ 的做法：先把“与”全都放在前 $k$ 个位置，记此时的答案为 $ans$。由于题目希望每个“与”运算符越靠右越好，对于前 $k$ 个“与”中的最后一个，枚举它放在 $n-1$ 到 $1$ 的答案是否等于 $ans$，如果等于就替换掉，否则不变。实现的时候用双指针，只会扫一遍，统计答案是 $O(n)$ 的。

思考怎么优化，对于 $k$ 个“与”运算的最后一个，从 $n-1$ 到 $1$ 枚举，最后的结果一定是一些“and”、一些“or”、一些“and”、一些“or”。其中的“or”也可能没有。我们可以用数据结构维护一下某段区间的按位与和按位或合，这样就能在较快的时间内统计该方案的答案。

那如果不是 $k$ 个“与”运算的最后一个呢？之前的最后一个已经被替换到其它位置去了。其实还是“and”一段区间的答案、“or”一段区间的答案、“and”一段区间的答案、“or”一段区间的答案的形式。每次在适配和失配的时候维护一下后两个答案即可，时间复杂度 $O(n\log n)$

✔道路修建 赛时调了两个小时暴力都没调出来

感觉这道题最重要的两个套路就是：把路径长度转化为边经过的次数，把边的信息挂在点上倍增处理。

首先有个很明显的性质，加了边后 $x$ 到 $lca$，以及 $y$ 到 $lca$ 路径上的点构成了一个环。可以把贡献看做两部分，一部分是“环边”产生的贡献，一部分是“环点子树内的边”产生的贡献，如下图：同种颜色的点在同一颗子树内。新加了一条边后，子树的性质也发生了改变（可能原来属于某个点的子树，但在我们统计答案时却不考虑）。

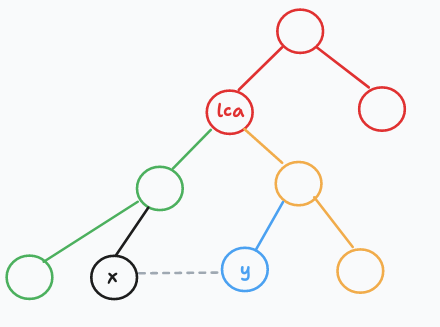
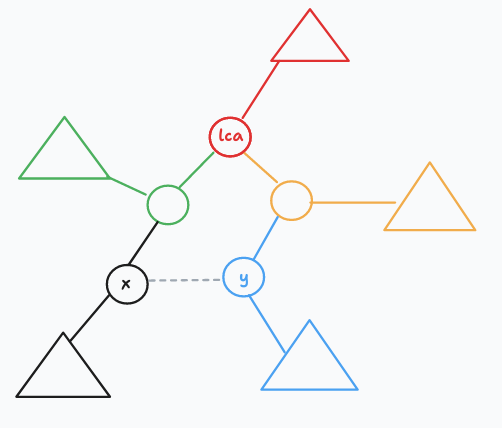
先处理出加边前的贡献，在加上加边后的贡献。加边前的贡献很好处理，dfs 的时候直接预处理就行了，每条边的贡献为 $si{z}_x\times (n-si{z}_x)$，其中 $x$ 为这条边指向的点。

以下我们的讨论基于 $x$ 与 $y$ 不在一条链上，在一条链上的时候也差不多（只是处理 $x、y、lca$ 的时候可能不一样）。

• “环边”产生的贡献

  考虑新加了一条边后，每一个点都可以经过两条路径到达与它不是同一颗子树内的点，则该答案为 $tot=len\times \frac{(n^2-\sum si{z}_x^2)}{2}$，其中 $len$ 为环的长度，后面一部分为在两颗不同子树内选点的方案数。瓶颈是快速处理 $\sum si{z}_x^2$ 的答案，通过观察发现，加边后每个点的 $si{z}_x=si{z}_x^{\prime }-si{z}_{to}^{\prime }$，其中 $si{z}^{\prime }$ 表示加边前的子树大小，$to$ 表示 $x$ 在环上的儿子。这个东西是与边相关的，我们把它挂在 $to$ 这个点上，倍增处理，特判 $x、y、lca$ 即可。

  但是这样我们发现对于一条“环边”，我们是把它在加边前的贡献也算进去了的，我们还需要减去这部分多算的，所以“环边”产生的总贡献为 $tot-\sum g_x$，其中 $g_x$ 表示指向 $x$ 的那条边的原来贡献，且 $x\ne lca$，同样是把它挂在指向的点上，我们可以在 dfs 时就预处理出 $g_x$ 的倍增数组。

• “环点子树内的边”产生的贡献

  首先为了计算这部分答案，我们肯定要对于每个“环点”预处理出其子树内每个点到它的距离，什么时候会产生贡献，就是考虑它到与它不在同一颗子树内的点的路径的时候。答案即为 $di{s}_x\times (n-si{z}_x)$，其中 $di{s}_x$ 表示“环点” $x$ 的子树内每一个点到它的距离，$di{s}_x=di{s}_x^{\prime }-di{s}_{to}^{\prime }-si{z}_{to}^{\prime }$，同样是挂在点上，倍增预处理，特判 $x、y、lca$。

  讲一下怎么特判 $lca$，我们对于每个节点 $x$ 记录一下如图绿色部分到 $x$ 的距离，记为 $u{p}_x$，$lca$ 的贡献即为 $(u{p}_{lca}+di{s}_{lca}^{\prime }-di{s}_x^{\prime }-di{s}_y^{\prime }-si{z}_x^{\prime }-si{z}_y^{\prime })\times (n-si{z}_x^{\prime }-si{z}_y^{\prime })$，其中 $x$ 表示 $x$ 往上跳，跳到的 $lca$ 下的第一个点，$y$ 表示 $y$ 往上跳，跳到的 $lca$ 下的第一个点。

  

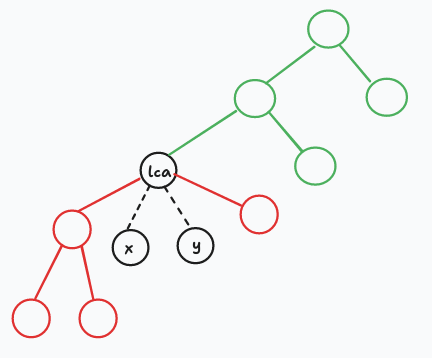
注意特判一下同一条链的清空即可。

code

#include<bits/stdc++.h>
#define int long long
#define pb push_back
#define pp pop_back
using namespace std;
const int maxn=3e5+5;
const int mod=998244353;
int read(int x=0,bool f=1,char c=0){
    while (!isdigit(c=getchar())) f=c^45;
    while (isdigit(c)) x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return f?x:-x;
}
vector<int>he[maxn];
int n,q,type,las,sum;
int d[maxn],siz[maxn],f[maxn][22];
int ans,dis[maxn],up[maxn],ny2;
int g1[maxn][22],g2[maxn][22],g3[maxn][22];
int qp(int x){return x*x%mod;}
int qpow(int a,int b){
    int res=1;
    while (b){
        if (b&1) res=res*a%mod;
        a=a*a%mod;b>>=1;
    }
    return res;
}
void dfs1(int x,int fa){
    d[x]=d[fa]+1;f[x][0]=fa;
    for (int j=1;j<=log2(n);j++)
        f[x][j]=f[f[x][j-1]][j-1];
    for (auto to:he[x])
        if (to!=fa){
            dfs1(to,x);siz[x]+=siz[to];
            dis[x]+=dis[to]+siz[to];
        }
}
void dfs2(int x,int fa){
    for (int j=1;j<=log2(n);j++){
        g1[x][j]=g1[x][j-1]+g1[f[x][j-1]][j-1];
        g2[x][j]=g2[x][j-1]+g2[f[x][j-1]][j-1];
        g3[x][j]=g3[x][j-1]+g3[f[x][j-1]][j-1];
        g1[x][j]%=mod;g2[x][j]%=mod;g3[x][j]%=mod;
    }
    for (auto to:he[x])
        if (to!=fa){
            g2[to][0]=siz[to]*(n-siz[to])%mod;
            up[to]=(up[x]+n-siz[to]+dis[x]-dis[to]-siz[to])%mod;
            g3[to][0]=(dis[x]-dis[to]-siz[to])%mod*(n-siz[x]+siz[to])%mod;
            g1[to][0]=qp(siz[x]-siz[to]);sum=(sum+g2[to][0])%mod;dfs2(to,x);
        }
}
int lca(int x,int y){
    if (x==y) return x;
    if (d[x]<d[y]) swap(x,y);
    for (int j=log2(d[x]);j>=0;j--)
        if (d[f[x][j]]>=d[y]) x=f[x][j];
    if (x==y) return x;
    for (int j=log2(d[x]);j>=0;j--)
        if (f[x][j]!=f[y][j]) 
            x=f[x][j],y=f[y][j];
    return f[x][0];
}
int getsiz2(int x,int y,int o){
    if (o){
        int res=qp(siz[x]);
        for (int j=log2(d[x]);j>=0;j--)
            if (d[f[x][j]]>d[y])
                res+=g1[x][j],x=f[x][j];
        return (res+qp(n-siz[x]))%mod;
    }
    int res=qp(siz[x])+qp(siz[y]);
    for (int j=log2(d[x]);j>=0;j--)
        if (d[f[x][j]]>=d[y])
            res+=g1[x][j],x=f[x][j];
    for (int j=log2(d[x]);j>=0;j--)
        if (f[x][j]!=f[y][j]){
            res+=g1[x][j]+g1[y][j];
            x=f[x][j];y=f[y][j];
        }
    return (res+qp(n-siz[x]-siz[y]))%mod;
}
int getsur(int x,int y,int o){
    int res=0;
    for (int j=log2(d[x]);j>=0;j--)
        if (d[f[x][j]]>=d[y])
            res+=g2[x][j],x=f[x][j];
    if (o) return res%mod;
    for (int j=log2(d[x]);j>=0;j--)
        if (f[x][j]!=f[y][j]){
            res+=g2[x][j]+g2[y][j];
            x=f[x][j];y=f[y][j];
        }
    return (res+g2[x][0]+g2[y][0])%mod;
}
int getdis(int x,int y,int o){
    if (o){
        int res=dis[x]%mod*(n-siz[x])%mod;
        for (int j=log2(d[x]);j>=0;j--)
            if (d[f[x][j]]>d[y])
                res+=g3[x][j],x=f[x][j];
        return (res+(dis[y]-dis[x]-siz[x]+up[y])%mod*siz[x]%mod)%mod;
    }
    int res=dis[x]%mod*(n-siz[x])%mod;
    res+=dis[y]%mod*(n-siz[y])%mod;
    for (int j=log2(d[x]);j>=0;j--)
        if (d[f[x][j]]>=d[y])
            res+=g3[x][j],x=f[x][j];
    for (int j=log2(d[x]);j>=0;j--)
        if (f[x][j]!=f[y][j]){
            res+=g3[x][j]+g3[y][j];
            x=f[x][j],y=f[y][j];
        }
    int tmp=up[f[x][0]]+dis[f[x][0]];
    tmp+=-dis[x]-dis[y]-siz[x]-siz[y];
    return (res+tmp%mod*(siz[x]+siz[y])%mod)%mod;
}
void solve(int x,int y,int lc){
    if (x==y) return ans=sum,void();
    if (d[x]<d[y]) swap(x,y);
    int len=d[x]+d[y]-2*d[lc]+1;
    bool t=(lc==y)?1:0;
    ans=sum+len*(qp(n)-getsiz2(x,y,t)+mod)%mod*ny2%mod;
    ans=(ans-getsur(x,y,t)+getdis(x,y,t)+mod)%mod;
}
signed main(){
    freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout);
    n=read();q=read();
    type=read();ny2=qpow(2,mod-2);
    for (int i=1,x,y;i<n;i++){
        x=read();y=read();siz[i]=1;
        he[x].pb(y);he[y].pb(x);
    }
    siz[n]=1;dfs1(1,0);dfs2(1,0);
    for (int i=1,x,y;i<=q;i++){
        x=read();y=read();
        if (type) x^=las,y^=las;
        ans=0;solve(x,y,lca(x,y));
        printf("%lld\n",ans);las=ans;
    }
}

11/2

✔网格 以为是签到题，赛后发现大家都没过

没手模第二个样例，导致题一直读假了，最后还剩 $15$ 分钟的时候才发现。

通过写暴力我们发现，在计算一种方案的值的时候，其实就是一堆乘积的和，我们只需要三个维护东西：当前的结果 $ans$（当前的和，不算没计算完的），最后的一段乘积 $len$，这个点的数字要算的次数 $res$。

$$ans=\{\begin{array}{ll}ans& s_i\ne \text{`+'}\\ ans+len& s_i=\text{`+'}\end{array}$$

$$len=\{\begin{array}{ll}0& s_i\notin [1,9]\\ len\times 10+s_i\times res& s_i\in [1,9]\end{array}$$

$$res=\{\begin{array}{ll}1& s_i=\text{`+'}\\ len& s_i=\text{`}\times \text{'}\\ res& s_i\in [1,9]\end{array}$$

那现在是要同时计算多种方案的值，我们 DP 就好。设 $f_{i,j}$ 表示当前的和，$no{w}_{i,j}$ 表示最后一段的数字/乘积，$g_{i,j}$ 表示这个点的数字要算的次数，同理转移即可。

$$f_{i,j}=\{\begin{array}{ll}{f}_{i-1,j}+f_{i,j-1}& a_{i,j}\ne \text{`+'}\\ f_{i-1,j}+f_{i,j-1}+no{w}_{i-1,j}+no{w}_{i,j-1}& a_{i,j}=\text{`+'}\end{array}$$

$$no{w}_{i,j}=\{\begin{array}{ll}0& a_{i,j}\notin [1,9]\\ (no{w}_{i,j-1}+no{w}_{i-1,j})\times 10+(g_{i,j-1}+g_{i-1,j})\times a_{i,j}& a_{i,j}\in [1,9]\end{array}$$

$$g_{i,j}=\{\begin{array}{ll}{C}_{i+j-2}^{i-1}& a_{i,j}=\text{`+'}\\ no{w}_{i,j-1}+no{w}_{i-1,j}& a_{i,j}=\text{`}\times \text{'}\\ g_{i,j-1}+g_{i-1,j}& a_{i,j}\in [1,9]\end{array}$$

✔矩形 数据比较水，很容易骗分

$O(n^2)$ 做法：灵感来源于之前模拟赛中的一道网格图数矩形的题，枚举对角线上的两个点，判断另外两个点是否存在即可。

赛时 $80$ 分：把 $x$ 相同的点全塞到一个 $\text{vector}$ 里（塞的是纵坐标 $y$）。每次枚举两个集合，求它们交集的个数，复杂度 $O(cnt{x}^{2}cnty)$，其中 $cntx$ 表示一共有多少个不同的横坐标 $x$，$cnty$ 表示集合元素个数的最大值，$cntx\times cnty\le n$。

正解：来源于 $O(cntx\times n)$ 的做法，实际上和上面的差不多，每次枚举一个集合，枚举其它的集合与它取交。我们要考虑的是减小 $cntx$，这里用的是根号分治。我们发现随着 $cnty$ 的增大，$cntx$ 是减小的，对于 $cnty\ge \sqrt{n}$ 的集合，我们采用上面的做法，此时的 $cntx\le \sqrt{n}$；那 $cnty<\sqrt{n}$ 的集合怎么办？我们考虑转一个向，把 $y$ 相同的点全塞到一个 $\text{vector}$ 里（塞的是横坐标 $x$），接下来同样是枚举集合取交，复杂度 $O(cnty\times n)$，总的时间复杂度就是 $O(n\sqrt{n})$ 的。

✔图书管理 签到题没签上

考虑每个 $p_i$ 会对哪些区间产生贡献，对于 $p_j>p_i(1\le j\le n,j\ne i)$ 的点，我们把 $a_j$ 赋为 $1$，对于 $p_j<p_i(1\le j\le n,j\ne i)$ 的点，我们把 $a_j$ 赋为 $-1$，特殊的 $a_i=0$。那么中位数为 $p_i$ 的区间就得满足：$\sum _{j=l}^r{a}_j=0$

对于 $i\le j\le n$ 的点处理出 $\sum _{k=i}^j{a}_k$ 的值，记为 $s_j$，用桶记一下。对于 $1\le j\le i$ 的点处理出 $\sum _{k=j}^i{a}_k$ 的值，记为 $t_j$。我们直接 $O(n)$ 扫一遍对于每个 $t_j$ 查询哪些 $s_j$ 的值为 $-t_j$ 即可，时间复杂度为 $O(n^2)$。

✔函数 感觉也是签到题

找出 $k1,k2$，其中 $k1\oplus a$ 为最小值，$k2\oplus a$ 为最大值。如果 $f(k1)\times f(k2)>0$，则肯定无解。

否则每次二分 $mid$，由于 $f(k1)\times f(k2)\le 0$，则 $f(k1)$ 与 $f(k2)$ 异号，$f(mid)$ 也肯定与其中的某一个异号。每次舍去一半的区间，复杂度为 $O(\log n)$。

找到 $k1,k2$ 可以用 trie 树，预处理 $O(n\log n)$，查询为 $O(\log n)$。综上复杂度为 $O((n+q)\log n)$