虚树【学习笔记】
为什么要用虚树？
例题
在某些树上问题中，对于某次询问，我们并不需要用到全部的树上的点：
例如，例题中：
总点数 \(n \le 2.5\times10^5\)
询问次数 \(m \le 5\times10^5\)
询问的点数 \(\sum k_i \le 5\times10^5\)
我们可以发现其实每次询问均摊下来的询问点数k并不多，但如果每次询问都用到全部的点，会超时
所以我们将所有的关键点拎出来建树，来确保时间复杂度的优秀
朴素做法
我们回到例题上来，可以想到如果树的点数很少时，我们可以直接用 \(DP\) ：
首先我们设某次询问中被选中的点（
资源丰富）为 关键点
\(dp_i\) 表示不让 \(i\) 与 \(i\) 的子树内任意一个关键点互通所需要的最小代价
\(w_{u,v}\) 表示连接 \(u\) 和 \(v\) 的边权
\(u\) 表示 \(i\) 连接的一个儿子节点
转移方程式：
- 当 \(u\) 是关键点时 : 你必须砍掉 \(i\) 到 \(u\) 的这条边
\(dp_i+=w_{i,u}\)
- 当 \(u\) 不是关键点时 ：你可以选择砍掉 \(i\) 到 \(u\) 的这条边或者让 \(u\) 不连接关键点
\(dp_i+=min(w_{i,u},dp_u)\)
此时时间复杂度为 \(O(nq)\) 肯定过不了，考虑用虚树建一颗更简洁的树（没有那么多用不到的点）
虚树做法
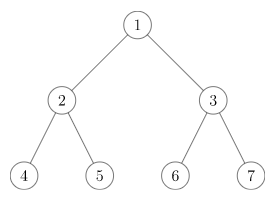
在原树中，我们可以发现大多数点是没用的，以下图为例：
如果我们选取的关键点是2,4：
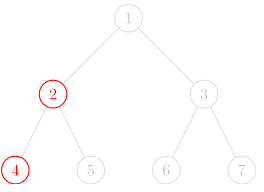
图中只有两个红色的点是关键点，而别的点全都是非关键点,对于这道题来说，我们只需要保证 1 号节点无法到达2,4就行了而 1 号节点的右子树没有一个关键点，我们没必要去DP它
观察题目给出的条件，红色点（关键点）的总数是与 n 同阶的，也就是说实际上一次询问中红色的点对于整棵树来说是很稀疏的，所以如果我们能让复杂度由关键点的总数来决定就好了
所以我们需要浓缩信息，只存储与答案相关的信息，把一整颗大树浓缩成小树
虚树长什么样？
这里我们主要通过一些图理解（感谢oiwiki我才不用画图）
下图中，红色结点是我们选择的关键点，红色和黑色结点都是虚树中的点（要把某些红色节点相连必须用到黑色节点），黑色的边是虚树中的边。
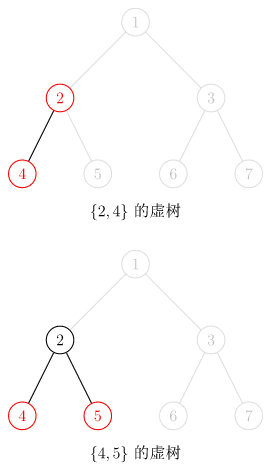
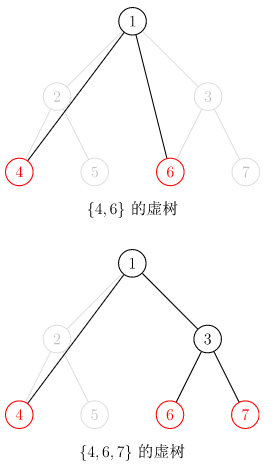
因为任意两个关键点的 \(lca\) 也是需要保存重要信息的，所以我们需要保存它们的 \(lca\)，因此虚树中不一定只有关键点。
怎么构造虚树？
这里介绍的是二次排序+ lca 连边的方法，还有一种单调栈的构造方法，详见oiwiki
- 将关键节点按照 \(dfs\)序 排序，并插入序列 \(a\)
- 关键节点中两两求 \(lca\)，插入序列 \(a\) 中
- 在将序列 \(a\) 按照 \(dfs\)序 排序，并去重
- 遍历序列 \(a\) ，枚举相邻两个点的编号（设为 \(x\) ，\(y\) ）求 \(lca\) ，建一条由 \(lca\) 指向 \(y\) 的边
为什么连接 \(LCA(x,y)\) 和 \(y\) 可以做到不重不漏呢？
证明：
如果 \(x\) 是 \(y\) 的祖先，那么 \(x\) 直接到 \(y\) 连边。因为 \(dfs\)序保证了 \(x\) 和 \(y\) 的 \(dfs\)序是相邻的，所以 \(x\) 到 \(y\) 的路径上面没有关键点。
如果 \(x\) 不是 \(y\) 的祖先，那么就把 \(lca(x,y)\) 当作 \(y\) 的的祖先，根据上一种情况也可以证明 \(lca(x,y)\) 到 \(y\) 点的路径上不会有关键点。
所以连接 \(lca(x,y)\) 和 \(y\)，不会遗漏，也不会重复。
另外第一个点没有被一个节点连接会不会有影响呢？因为第一个点一定是这棵树的根，所以不会有影响，所以总边数就是 \(m-1\) 条。
因为至少要两个实点才能够召唤出来一个虚点，再加上一个根节点，所以虚树的点数就是实点数量的两倍。
时间复杂度 \(O(klog_n)\)，其中 \(k\) 为关键点数，\(n\) 为总点数。
实现：
int dfn[maxn]
int h[maxn], a[maxn], cnt; // 存储关键点
bool cmp(int x,int y){
return dfn[x]<dfn[y];
}
void buid{
h[++k]=1;//为了方便，我们首先将1号节点加入虚树中
sort(h+1,h+1+k,cmp);//操作1，按照dfs序排序
for (int i=1; i<=k; i++) {
a[++cnt]=h[i];//将关键点插入序列a
if (i==k) break;
//操作2,两两求lca插入序列a中
a[++cnt]=lca(h[i],h[i+1]);
}
sort(a+1,a+1+cnt,cmp);//操作3，排序
cnt=unique(a+1,a+1+cnt)-(a+1);//去重
for (int i=1; i<cnt; i++) {
int lc=lca(a[i],a[i+1]);
add(lc,a[i+1],0);//操作4，连一条由lca(x，y)指向y的边
}
}
回到例题
虚树建好后，这道题就很好攻克了
设 \(miv_i\) 表示 \(i\) 到 1 号节点边权最小的一条边（容易理解的是：割掉这条边后，\(i\) 就不再与 1 号节点相连了）
\(col_i\)记录 \(i\) 是否为关键点（是关键点为1，否则为0）
- \(miv\) 和一些其他数组的预处理
void dfs1(int x,int fa){
vis[x]=1;
dfn[x]=++cnt;
for (int i=he[x];i;i=ne[i])
if (!vis[to[i]]){
d[to[i]]=d[x]+1;
f[to[i]][0]=x;
miv[to[i]]=min(miv[x],w[i]);
dfs1(to[i],x);
}
he[x]=0;
}
- 求解让 1 号节点不与( \(x\) 及 \(x\) 的子树中的关键点)连通的最小代价
int dfs2(int x,int fa){
int tmp=0,ans;
for (int i=he[x];i;i=ne[i])
tmp+=dfs2(to[i],x);
if (col[x]) ans=miv[x];
else ans=min(miv[x],tmp);
he[x]=0;col[x]=0;
//多次询问，可以在递归中直接清空
return ans;
}
完整代码(*╹▽╹*)
#include<bits/stdc++.h>
#define int long long
#define pai pair<int,int>
#define mk make_pair
#define fi first
#define se second
using namespace std;
const int maxn=1e6+10;
const int N=30;
const int INF=1e18;
int read(){
int x=0,f=1;char c=getchar();
while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
while (c>='0'&&c<='9') {x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
int tot,n,q,cnt,k,d[maxn];
int miv[maxn],dfn[maxn];
int he[maxn],w[maxn<<1];
int ne[maxn<<1],to[maxn<<1];
int h[maxn],a[maxn];
int f[maxn][N];
bool col[maxn],vis[maxn];
void add(int u,int v,int z){
ne[++tot]=he[u];
he[u]=tot;
to[tot]=v;
w[tot]=z;
}
bool cmp(int x,int y){
return dfn[x]<dfn[y];
}
void dfs1(int x,int fa){
vis[x]=1;
dfn[x]=++cnt;
for (int i=he[x];i;i=ne[i])
if (!vis[to[i]]){
d[to[i]]=d[x]+1;
f[to[i]][0]=x;
miv[to[i]]=min(miv[x],w[i]);
dfs1(to[i],x);
}
he[x]=0;
}
void init(){
for (int j=1;j<=20;j++)
for (int i=1;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1];
}
int lca(int x,int y){
if (x==y) return x;
if (d[x]<d[y]) swap(x,y);
for (int j=log2(d[x]);j>=0;j--)
if (d[f[x][j]]>=d[y])
x=f[x][j];
if (x==y) return x;
for (int j=log2(d[x]);j>=0;j--)
if (f[x][j]!=f[y][j])
x=f[x][j],y=f[y][j];
return f[x][0];
}
int dfs2(int x,int fa){
int tmp=0,ans;
for (int i=he[x];i;i=ne[i])
tmp+=dfs2(to[i],x);
if (col[x]) ans=miv[x];
else ans=min(miv[x],tmp);
he[x]=0;col[x]=0;
return ans;
}
signed main(){
n=read();
for (int i=1,x,y,z;i<n;i++){
x=read();y=read();z=read();
add(x,y,z);add(y,x,z);
}
d[0]=-INF,miv[1]=INF;
dfs1(1,0);init();q=read();
while (q--){
k=read();tot=cnt=0;
for (int i=1,x;i<=k;i++){
x=read();
h[i]=x;
col[x]=1;
}
h[++k]=1;
sort(h+1,h+1+k,cmp);
for (int i=1;i<=k;i++){
a[++cnt]=h[i];
if (i==k) break;
a[++cnt]=lca(h[i],h[i+1]);
}
sort(a+1,a+1+cnt,cmp);
cnt=unique(a+1,a+1+cnt)-(a+1);
for (int i=1;i<cnt;i++){
int lc=lca(a[i],a[i+1]);
add(lc,a[i+1],0);
}
printf("%lld\n",dfs2(1,0));
for (int i=1;i<=cnt;i++)
he[i]=0,col[i]=0;
}
return 0;
}
