线段树优化建图
为什么？
什么时候用线段树优化建图
例题
如果此时暴力建边 \(O(n^{2})\) 肯定会 TLE
观察到题目中的“区间”此时考虑用线段树优化建图，在每个区间上连边（线段树上只有 \(\log{n}\) 个区间）来减少边的个数
实现方法？
摘抄自 tzx_wk
我们就拿 \(2\) 操作来举例吧。现在假设假如有一个点要与 \([1,3]\) 的点连边权为 \(w\) 的边，那么我们建出线段树：
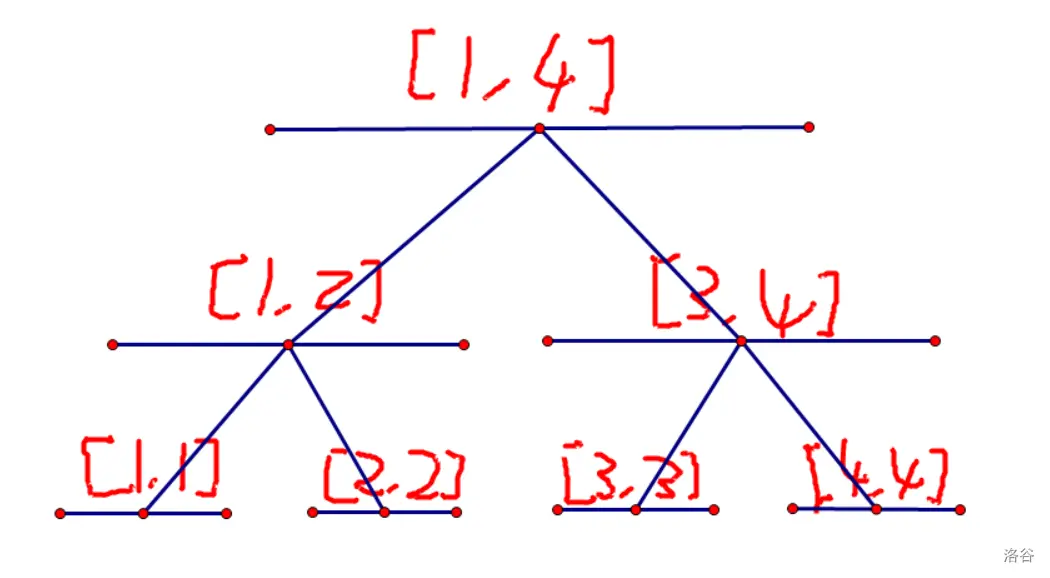
将 \([1,3]\) 拆成 \([1,2]\) 与 \([3,3]\) 然后分别连边，边权为 \(w\)（图中橙色的边）：
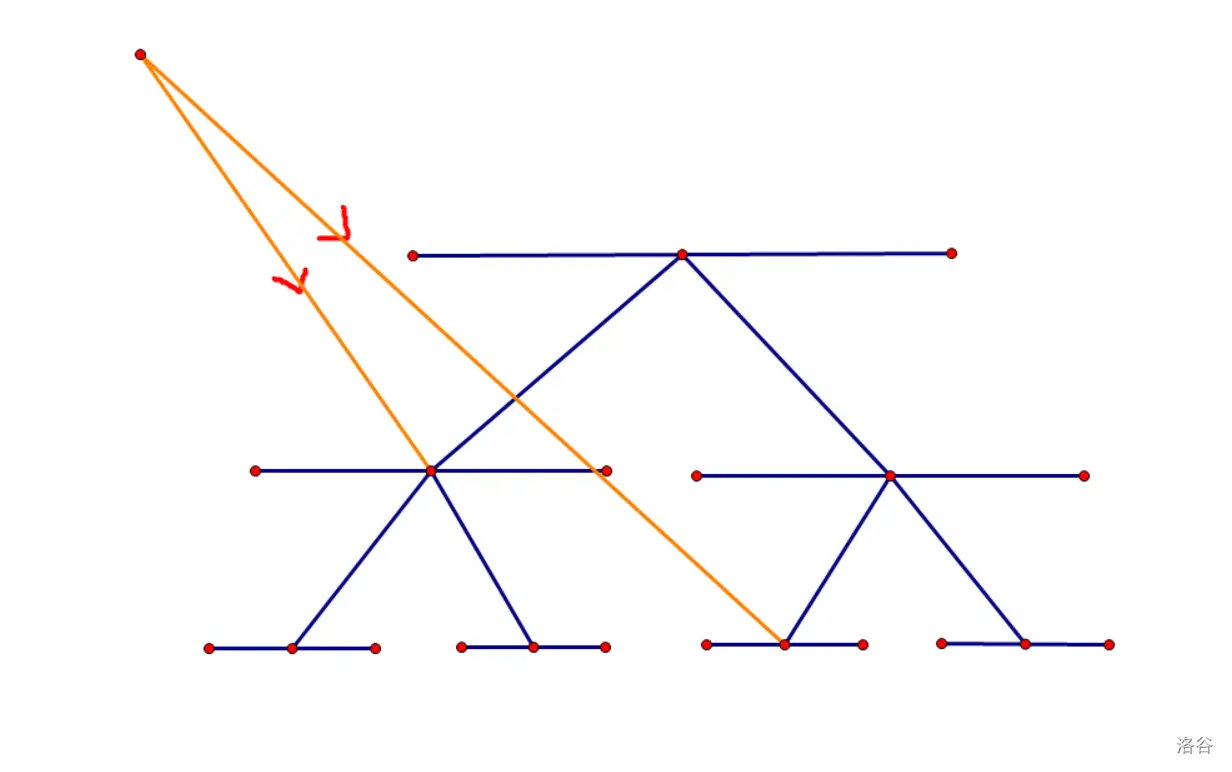
但是仅仅只连这两条边是远远不够的，因为你只将这个点与一个区间表示的点连了边，并没有将其连到具体的单点上。
因此我们还从每个区间向其子区间连边，由于你向下走，从一个大区间对应到一个小区间没有代价，因此这些边的边权为 \(0\) 。
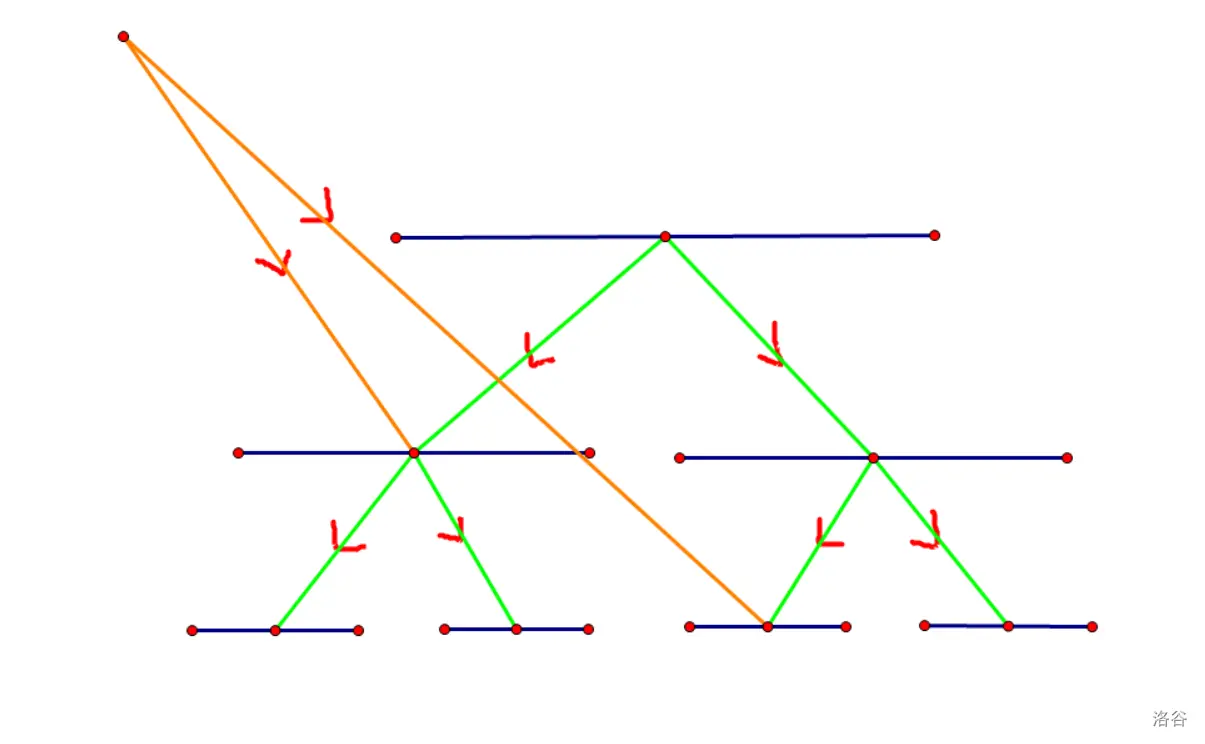
操作 \(3\) 也同理，只不过把之前连的所有边都反向。
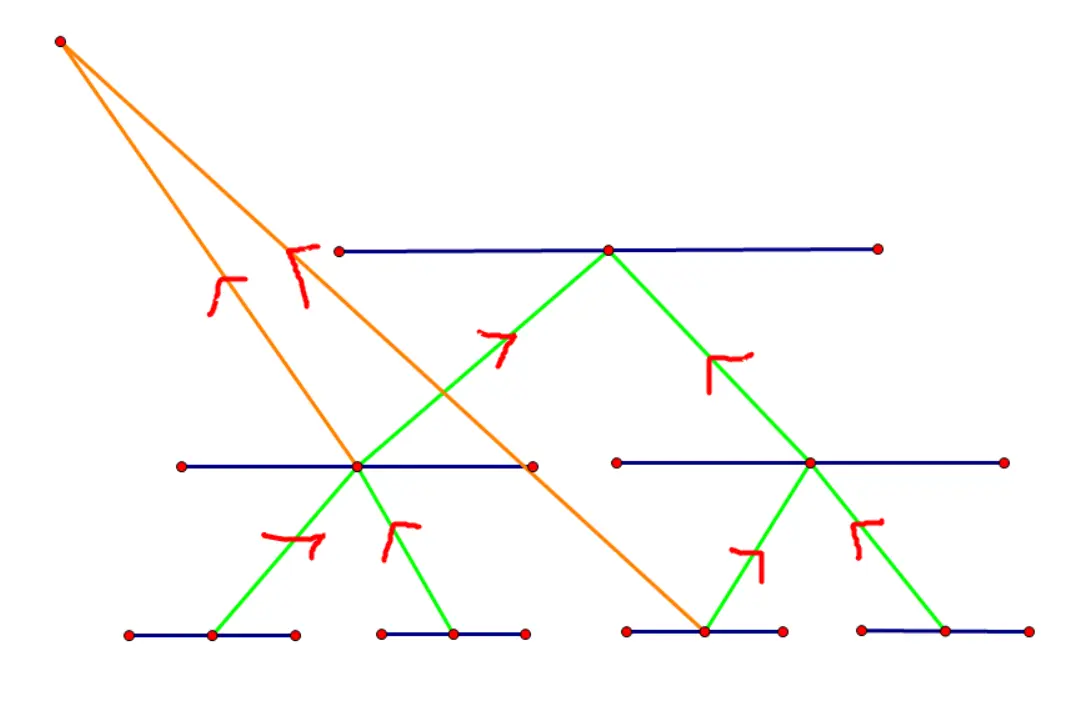
以上是操作 \(2\) 与操作 \(3\) 分开来考虑的情形，那么操作 \(2\) 与操作 \(3\) 相结合该怎么办呢？
显然你不能把它们揉在一棵线段树上，因为你线段树上每条边向上向下边权都为 \(0\)，故从原点到每个点的最短路也为 \(0\)，这……还玩个什么啊。。。。。。
因此可以想到建两棵线段树，第一棵只连自上而下的边，第二棵只连自下而上的边：
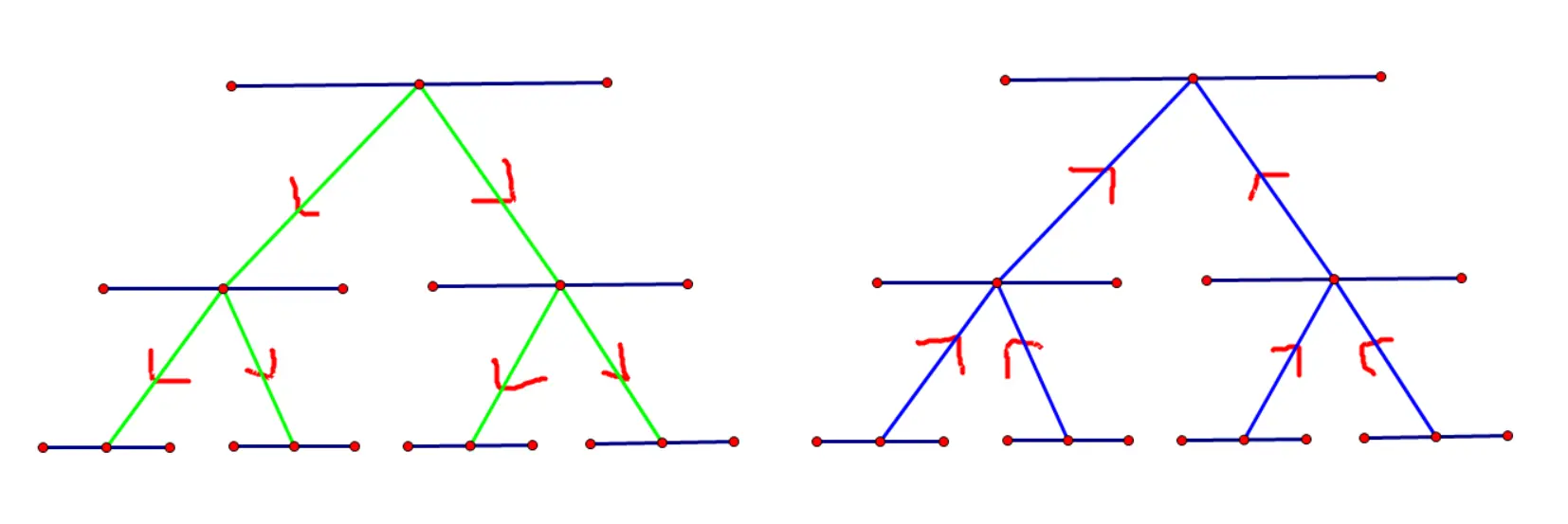
对于 \(2\) 操作，你就从第二棵线段树的叶子节点向第一棵线段树中的对应区间连边（下图中橙色的边）。
对于 \(3\) 操作，你就从第二棵线段树中的对应区间向第一棵线段树中的叶子节点连边（下图中粉色的边）。
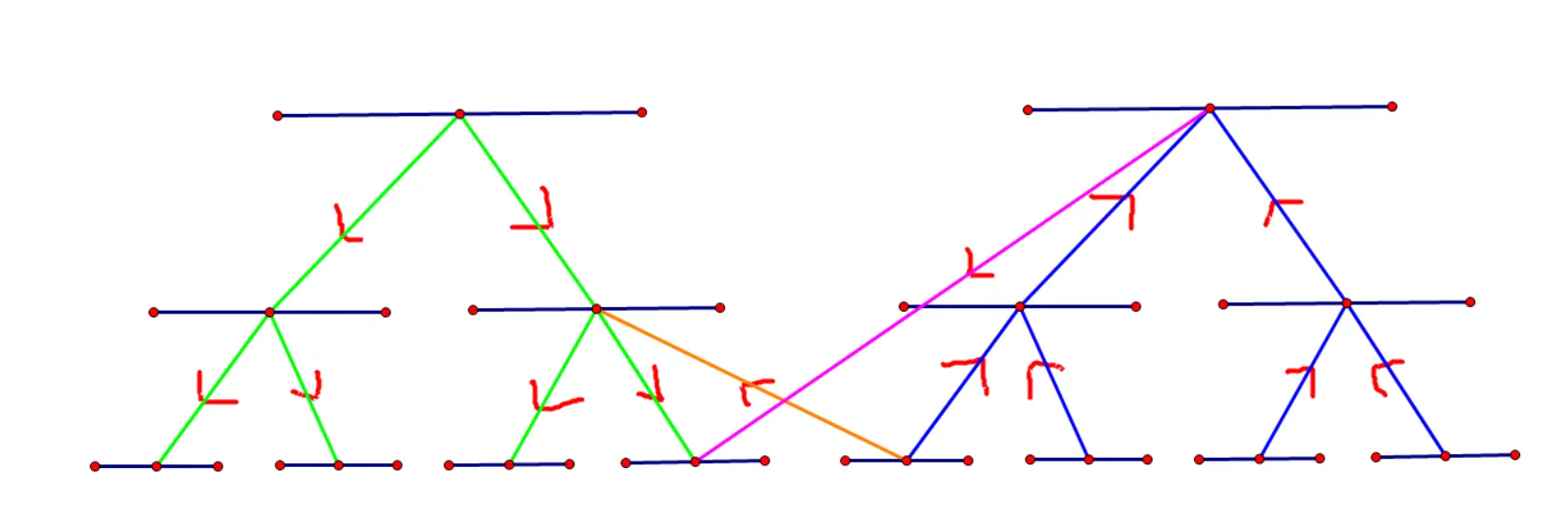
还有一点，就是两棵线段树的叶子节点实际上是同一个点，因此要在它们互相之间连边权为 \(0\) 的边（下图中黄色的边）
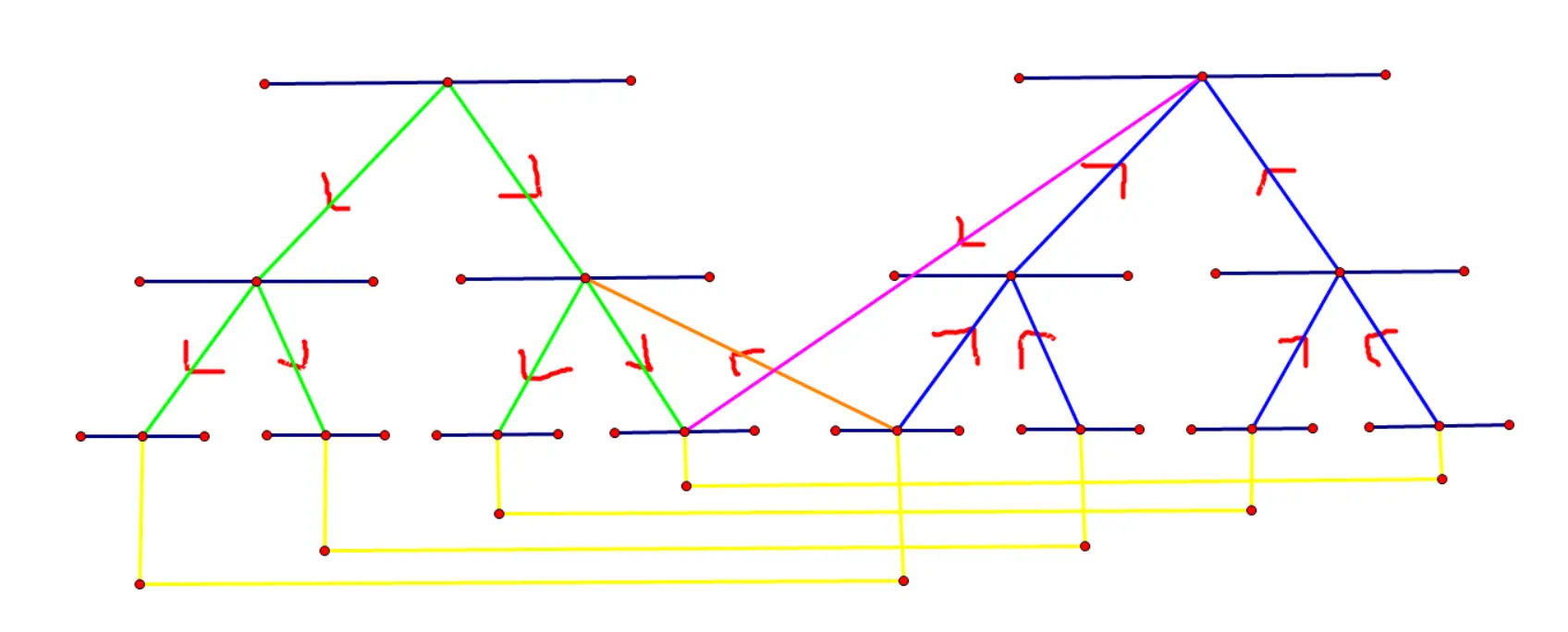
以上就是实现过程的思路。
代码？
1. 建树过程
- 首先我们要建两颗树，如下，\(op=2\) 时建入树（从点向区间连边），\(op=3\) 时建出树（从区间向点连边）
- 最底层的叶子节点编号为 \(1\) 到 \(n\) （这样就不用在两颗线段树的叶子节点间连边了）,其它节点在建树时由 \(cnt\) (初值为 \(n\) )再为节点编号赋初值
- 因为节点编号不满足 \(ls=rt<<1\), \(rs=rt<<1|1\),所以我们用 \(ls[rt]\) 和 \(rs[rt]\) 数组存儿子节点的编号
- 别忘了在线段树内部的连边
#define l(x) tr[x].l
#define r(x) tr[x].r
struct node{
int l,r;
}tr[maxn*4];
int cnt,rt1,rt2,ls[maxn*4],rs[maxn*4];
void build(int &rt,int l,int r,int op)
{
if (l==r) {rt=l;l(rt)=r(rt)=l;return ;}
rt=++cnt;l(rt)=l;r(rt)=r;int mid=(l+r)>>1;
build(ls[rt],l,mid,op);build(rs[rt],mid+1,r,op);
if (op==2) addedge(rt,ls[rt],0),addedge(rt,rs[rt],0);//入树，自上而下
else addedge(ls[rt],rt,0),addedge(rs[rt],rt,0);//出树，自下而上
}
2.实现操作中的建边
我们用 \(update\) 每次递归连边实现就好，根据op的值实现操作 \(2\) 和 \(3\)
void update(int rt,int l,int r,int x,int z,int op)
{
if (l<=l(rt)&&r(rt)<=r)
{
if (op==2) addedge(x,rt,z);
else addedge(rt,x,z);
return ;
}
int mid=(tr[rt].l+tr[rt].r)>>1;
if (l<=mid) update(ls[rt],l,r,x,z,op);
if (mid<r) update(rs[rt],l,r,x,z,op);
}
3.最短路
跑一遍正常的 \(dijkstra\) 就好
int n,q,s,dis[maxn*4];
bool vis[maxn*4];
struct point{
int dis,id;
bool operator < (const point &a) const{
return dis>a.dis;
}
};
void dij(int s)
{
priority_queue<point>q;
memset(dis,0x3f,sizeof(dis));
dis[s]=0;q.push(point{0,s});
while (!q.empty())
{
int x=q.top().id;q.pop();
if (vis[x]) continue;
vis[x]=1;
for (int i=he[x];i;i=ne[i])
if (!vis[to[i]]&&dis[x]+w[i]<dis[to[i]])
{
dis[to[i]]=dis[x]+w[i];
q.push(point{dis[to[i]],to[i]});
}
}
}
完整代码
#include<bits/stdc++.h>
#define int long long
#define l(x) tr[x].l
#define r(x) tr[x].r
using namespace std;
const int maxn=1e5+10;
const int INF=4557430888798830399;
int read()
{
int x=0,f=1;char c=getchar();
while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
while (c>='0'&&c<='9') {x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
int tot,he[maxn*4],ne[maxn*20];
int to[maxn*20],w[maxn*20];
struct node{
int l,r;
}tr[maxn*4];
void addedge(int u,int v,int z)
{
ne[++tot]=he[u];
he[u]=tot;
to[tot]=v;
w[tot]=z;
}
int cnt,rt1,rt2,ls[maxn*4],rs[maxn*4];
void build(int &rt,int l,int r,int op)
{
if (l==r) {rt=l;l(rt)=r(rt)=l;return ;}
rt=++cnt;l(rt)=l;r(rt)=r;int mid=(l+r)>>1;
build(ls[rt],l,mid,op);build(rs[rt],mid+1,r,op);
if (op==2) addedge(rt,ls[rt],0),addedge(rt,rs[rt],0);//入树，自上而下
else addedge(ls[rt],rt,0),addedge(rs[rt],rt,0);//出树，自下而上
}
void update(int rt,int l,int r,int x,int z,int op)
{
if (l<=l(rt)&&r(rt)<=r)
{
if (op==2) addedge(x,rt,z);
else addedge(rt,x,z);
return ;
}
int mid=(tr[rt].l+tr[rt].r)>>1;
if (l<=mid) update(ls[rt],l,r,x,z,op);
if (mid<r) update(rs[rt],l,r,x,z,op);
}
int n,q,s,dis[maxn*4];
bool vis[maxn*4];
struct point{
int dis,id;
bool operator < (const point &a) const{
return dis>a.dis;
}
};
void dij(int s)
{
priority_queue<point>q;
memset(dis,0x3f,sizeof(dis));
dis[s]=0;q.push(point{0,s});
while (!q.empty())
{
int x=q.top().id;q.pop();
if (vis[x]) continue;
vis[x]=1;
for (int i=he[x];i;i=ne[i])
if (!vis[to[i]]&&dis[x]+w[i]<dis[to[i]])
{
dis[to[i]]=dis[x]+w[i];
q.push(point{dis[to[i]],to[i]});
}
}
}
signed main()
{
n=read();q=read();s=read();
cnt=n;build(rt1,1,n,2);build(rt2,1,n,3);
for (int i=1,op,v,u,z,l,r;i<=q;i++)
{
op=read();
if (op==1)
{
v=read();u=read();
z=read();addedge(v,u,z);
}
else
{
v=read();l=read();r=read();z=read();
update(op==2?rt1:rt2,l,r,v,z,op);
}
}
dij(s);
for (int i=1;i<=n;i++)
if (dis[i]==INF) printf("-1 ");
else printf("%lld ",dis[i]);
return 0;
}
