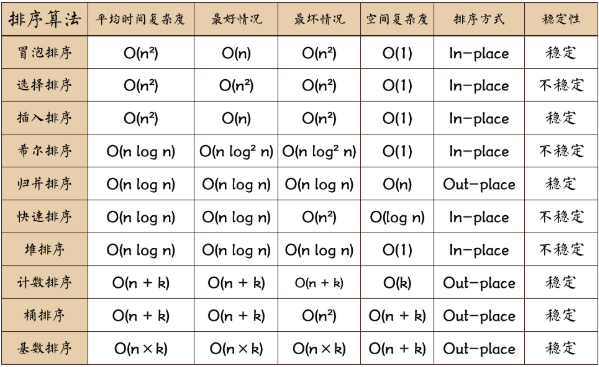
排序
1. 自己的写法, 不稳定, O(n2)
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return; } for(int i = 0;i<nums.length-1;i++){ for(int j = i+1;j<nums.length;j++){ if(nums[i]>nums[j]){ int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } } } }
2. 冒牌排序, 稳定 ,O(n2)
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return ; } for(int i = 0;i<nums.length-1;i++){ for(int j = 0;j<nums.length-i-1;j++){ if(nums[j]>nums[j+1]){ int temp = nums[j]; nums[j] = nums[j+1]; nums[j+1] = temp; } } } }
设置标记
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return ; } for(int i = 0;i<nums.length-1;i++){ boolean flag = false;//设置标记 for(int j = 0;j<nums.length-i-1;j++){ if(nums[j]>nums[j+1]){ int temp = nums[j]; nums[j] = nums[j+1]; nums[j+1] = temp; flag = true; } } if(!flag) break;//没有数据交换,提前退出 } }
3. 简单选择排序 ,不稳定 51,52,1->1,52,51 , O(n2)
该方法只是选择排序只有在确定了最小数的前提下才进行交换,大大减少了交换的次数。
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return ; } for(int i = 0;i<nums.length-1;i++){ int min = i; for(int j = i+1;j<nums.length;j++){ min = nums[j]<nums[min]?j:min; } if(min!=i){ int temp = nums[min]; nums[min] = nums[i]; nums[i] = temp; } } }
4. 插入排序 稳定 O(n2)
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return; } for(int i = 1;i<nums.length;i++){ int target = nums[i]; int j = i; while(j>0&&nums[j-1]>target){ nums[j] = nums[j-1]; j--; } nums[j]=target; } }
折半插入排序,使用二分查找优化插入排序
public int[] sortArray(int[] nums) {
if(null==nums||0==nums.length){
return nums;
}
for(int i = 1;i<nums.length;i++){
int target = nums[i];
int left = 0;
int right =i-1;
while(left<=right){
int mid =(left + right)/2;
if(nums[mid]<=target){
left = mid+1;
}
else{
right = mid-1;
}
}
for(int j = i;j>left;j--){
nums[j] = nums[j-1];
}
nums[left]=target;
}
return nums;
}
5. 快速排序 ,不稳定 5,11,12->12,11,5,O(nlgn)
使用分治的思想,
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return ; } quickSort(nums,0,nums.length-1); } private void quickSort(int[] nums ,int left,int right){ if(left>=right){ return; } int target = partition(nums,left,right); quickSort(nums,left,target-1); quickSort(nums,target+1,right); } private int partition(int[] nums,int left,int right){ int target = nums[left]; while(left<right){ while(left<right&&nums[right]>=target){ right--; } nums[left]=nums[right]; while(left<right&&nums[left]<=target){ left++; } nums[right] = nums[left]; } nums[left]=target; return left; }
6.堆排序,不稳定,O(nlgn)
public int[] sortArray(int[] nums) { if(null==nums||0==nums.length){ return nums; } //建立大顶堆 for(int i=nums.length/2;i>=0;i--){ heapAdjust(nums,i,nums.length-1); } for(int i=nums.length-1;i>0;i--){//将堆顶元素与末位交换,重新调整最大堆 int temp = nums[0]; nums[0]= nums[i]; nums[i] =temp; heapAdjust(nums,0,i-1); } return nums; } private void heapAdjust(int[] nums ,int left,int right){ int target = nums[left]; for(int i = left*2+1;i<=right;i=2*i+1){ //节点i左右孩子结点分别是2*i+1,2*i+2 if(i<right && nums[i]<nums[i+1]){//选择出左右孩子的较大值 i++; } if(target >=nums[i]){ break;//已是大顶堆 } nums[left] = nums[i]; left= i; } nums[left] = target; }
7. 希尔排序,不稳定,O(nlgn)
插入排序的一种高效率实现
public void sortArray(int[] nums) { if(null==nums||0==nums.length){ return ; } int d = nums.length/2; while(d>0){ for(int i=d;i<nums.length;i++){ int temp =nums[i]; int j = i-d; while(j>=0&&nums[j]>temp){ nums[j+d] = nums[j]; j-=d; } nums[j+d] = temp; } d /= 2; } }
8. 归并排序,稳定,空间复杂度为O(n),时间复杂度为O(nlogn)
public int[] sortArray(int[] nums) { if(null==nums||0==nums.length){ return nums; } mergeSort(nums,0,nums.length-1); return nums; } private void mergeSort(int[] nums,int left,int right){ if(left>=right){ return; } int mid= (left + right)/2;//若left+right溢出 可以优化为left+(right-left)/2 mergeSort(nums,left,mid); mergeSort(nums,mid+1,right); merge(nums,left,mid,right); } private void merge(int[] nums,int left,int mid,int right){ int[] temp = new int[right-left+1]; int i = left; int j = mid+1; int k = 0; while(i<=mid&&j<=right){ if(nums[i]<nums[j]){ temp[k]= nums[i]; i++; } else{ temp[k]= nums[j]; j++; } k++; } while(i<=mid){ temp[k++] = nums[i++]; } while(j<=right){ temp[k++] = nums[j++]; } for(int l =0;l<temp.length;l++){ nums[left+l] = temp[l]; } }
合并是可通过哨兵减少while循环
private void merge(int[] nums,int left,int mid,int right){ int[] arr1= new int[mid-left+2];//多加一个数即哨兵 int[] arr2 = new int[right-mid+1]; for(int i=left;i<=mid;i++){ arr1[i-left] = nums[i]; } for(int i=mid+1;i<=right;i++){ arr2[i-mid-1] = nums[i]; } int max = nums[mid]>nums[right]?nums[mid]:nums[right]; arr1[arr1.length-1] = max;//哨兵设为最大值,若不担心溢出可设为max+1 arr2[arr2.length-1] = max; int i = 0; int j = 0 ; int k = left; while(k<=right){ if(arr1[i]<=arr2[j]&&i<arr1.length-1){ nums[k]= arr1[i]; i++; } else{ nums[k]= arr2[j]; j++; } k++; } }
9.计数排序
public int[] sortArray(int[] nums) { if(null==nums||0==nums.length){ return nums; } int min = nums[0]; int max = nums[0]; for(int i =1;i<nums.length;i++){ min = min>nums[i]?nums[i]:min; max = max>nums[i]?max:nums[i]; } int[] count = new int[max - min +1]; Arrays.fill(count,0); for(int i = 0;i<nums.length;i++){ count[nums[i]-min]++; } int k =0; for(int i = 0;i<count.length;i++){ for(int j =0;j<count[i];j++){ nums[k++] = i+min; } } return nums; }
10 桶排序
计数排序是桶排序的一种特殊写法
public int[] sortArray(int[] nums) { if(null==nums||0==nums.length){ return nums; } int min = nums[0]; int max = nums[0]; for(int i =1;i<nums.length;i++){ min = min>nums[i]?nums[i]:min; max = max>nums[i]?max:nums[i]; } int bucketSize = 100;//桶的大小可作为参数调整, int bucketCount = (max-min)/bucketSize+1; ArrayList<ArrayList<Integer>> bucket = new ArrayList<>(bucketCount); for(int i= 0;i<bucketCount;i++){ bucket.add(new ArrayList<Integer>()); } for(int i = 0;i<nums.length;i++){ bucket.get((nums[i]-min)/bucketSize).add(nums[i]); } int k =0; for(int i = 0;i<bucket.size();i++){ //对桶排序 if(bucket.get(i).size()>1){ Collections.sort(bucket.get(i)); } //还原桶 for(int j =0;j<bucket.get(i).size();j++){ nums[k++] = bucket.get(i).get(j); } } return nums; }