算法 ----- 希尔排序

希尔排序 Shell Sort

介绍：

　　希尔排序（Shell Sort）也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。
　　该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高。

执行流程：
　　首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1[一组内数据间隔是d1构成的分组]，在各组内进行直接插入排序；
　　取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。
　　通常每一次分组间隔都是上一次分组的一半，直到最后为1直接执行插入排序！

举例：

　　我们来看下希尔排序的基本步骤，在此我们选择增量gap=length/2，缩小增量继续以gap = gap/2的方式，这种增量选择我们可以用一个序列来表示，{n/2,(n/2)/2...1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。

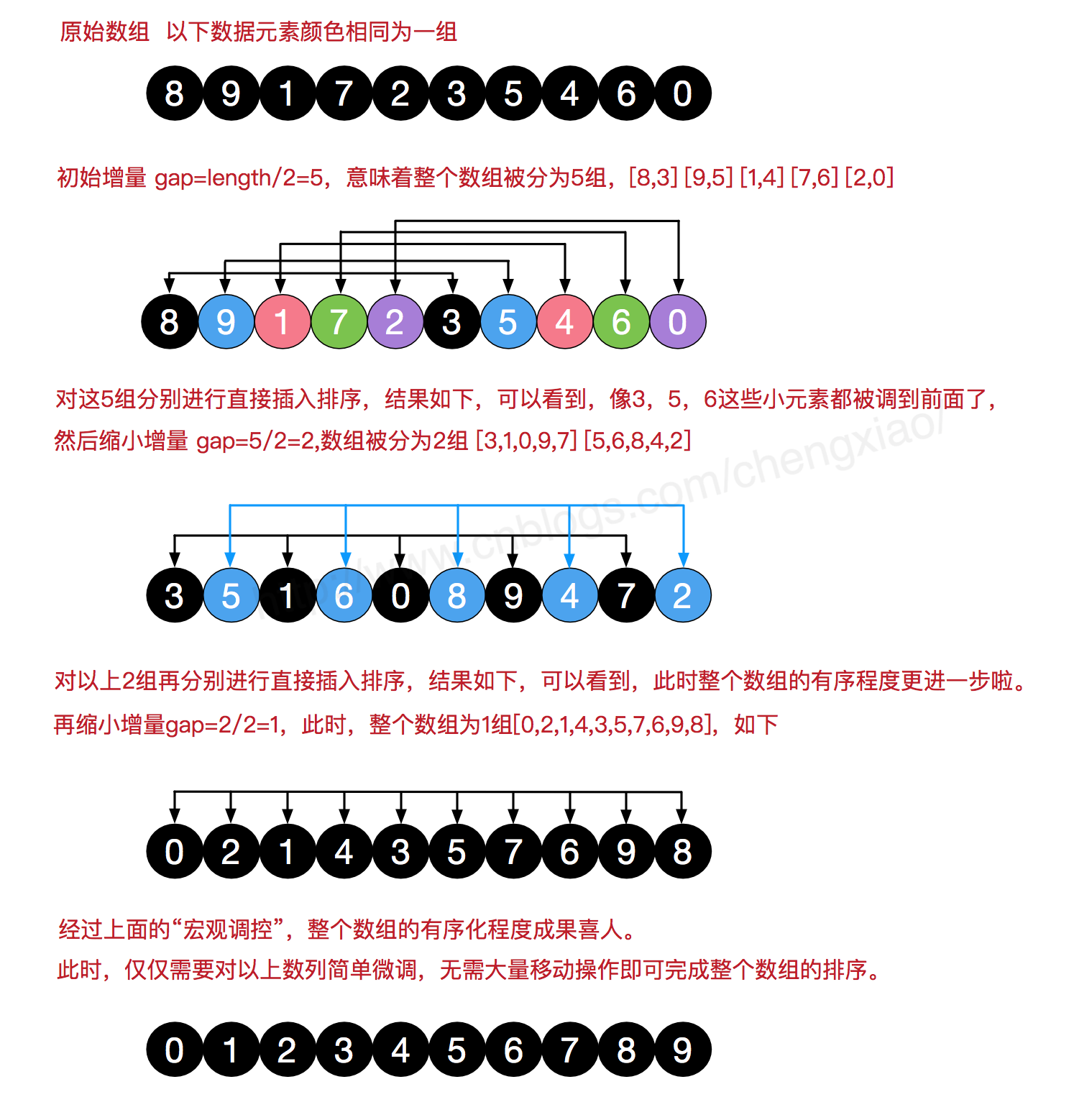
希尔排序动态展示：

算法实现：

def shell_sort(li):
    """
    希尔算法 分组插入算法，逐渐有序
    :param li: 无序列表
    :return: 有序列表
    """
    gap = len(li) // 2 #初始分组间隔
    while gap > 0:
        #组内排序
        # 以0~(gap-1)位的数作为各自分组的第一个数
        for i in range(gap, len(li)): #从gap位开始与自己组内数据比较
            tmp = li[i] #获取当前位置的值
            j = i - gap #自己所在分组，间隔为gap的值
            while j >= 0 and tmp < li[j]: #比较，如果当前值比前一个值小
                li[j + gap] = li[j] #把大的值赋给当前位置
                j -= gap #再去当前组内间隔为gap的值比较
            li[j + gap] = tmp #否则的话就不变
        #当前分组内值比较完成
        gap = gap // 2 #间隔减半，组内再排序

    return li

总结：
　　希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。
　　希尔排序是一种分组插入排序算法。将原数据集合分割成若干个子序列，然后再对子序列分别进行直接插入排序，使子序列基本有序，最后再对全体记录进行一次直接插入排序。
　　最关键的是跳跃和分割的策略，也就是我们要怎么分割数据，间隔多大的问题。通常将相距某个“增量”的记录组成一个子序列，这样才能保证在子序列内分别进行直接插入排序后得到的结果是基本有序而不是局部有序。

希尔排序的时间复杂度为： O(1.3n)