前缀树
何为前缀树?如何生成前缀树?
例子:
一个字符串类型的数组arr1,另一个字符串类型的数组arr2。
arr2中有哪些字符,是arr1中出现的?请打印。
arr2中有哪些字符,是作为arr1中某个字符串前缀出现的?请打印。
arr2中有哪些字符,是作为arr1中某个字符串前缀出现的?请打印arr2中出现次数最大的前缀。
又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。
典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
前缀树节点
//前缀树节点 public static class TrieNode { public int path;//在加前缀树的时候,这个节点到达过(通过)多少次 public int end; //这个节点是否是一个字符串结尾的节点,如果是的话它是多少个字符串结尾的节点 public TrieNode[] nexts; //如果路(字符种类)不止26条,可以以使用HashMap<Char,Node> nexts;算法一样,coding细节会有不同 //如果希望路与路之间不是像HashMap分散表达,而是连着的,可以使用TreeMap来表示 public TrieNode() { path = 0; end = 0; // nexts[0] == null 没有走向'a'的路 // nexts[0] != null 有走向'a'的路 // ... // nexts[25] == null 没有走向'z'的路 // nexts[25] != null 有走向'z'的路 //提前建了26条路,通过看下级有没有节点就知道后面有没有路 nexts = new TrieNode[26]; } }
图解:
根节点上p=4:
1、表示有多少(4)个以空字符串为前缀的字符串
2、表示前缀树中一共有多少(4)个字符串
3、若根节点上e=0,表示前缀树中有1个空字符串
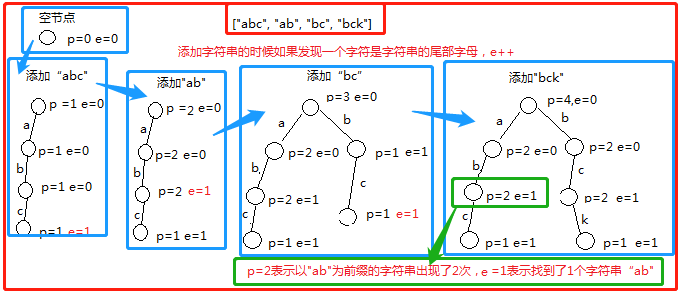
前缀树相关操作:
package Algorithms; public class TrieTree { //前缀树节点 public static class TrieNode { public int path;//在加前缀树的时候,这个节点到达过(通过)多少次 public int end; //这个节点是否是一个字符串结尾的节点,如果是的话它是多少个字符串结尾的节点 public TrieNode[] nexts; //如果路(字符种类)不止26条,可以以使用HashMap<Char,Node> nexts;算法一样,coding细节会有不同 //如果希望路与路之间不是像HashMap分散表达,而是连着的,可以使用TreeMap来表示 public TrieNode() { path = 0; end = 0; // nexts[0] == null 没有走向'a'的路 // nexts[0] != null 有走向'a'的路 // ... // nexts[25] == null 没有走向'z'的路 // nexts[25] != null 有走向'z'的路 //提前建了26条路,通过看下级有没有节点就知道后面有没有路 nexts = new TrieNode[26]; } } //前缀树 public static class Trie { private TrieNode root; //新建类的时候会初始化一个根节点 public Trie() { root = new TrieNode(); } public void insert(String word) { if (word == null) { return; } char[] chs = word.toCharArray(); // "abc" -> ['a', 'b', 'c'] TrieNode node = root; //node从根节点出发 node.path++; //来到根节点后,path = 1 int index = 0; for (int i = 0; i < chs.length; i++) { //从左往右遍历字符 index = chs[i] - 'a'; //由字符,对应走向哪条路 index = 'a'-'a'=0 (把字符转化为了ASCII码) if (node.nexts[index] == null) { //没有走向a的路 node.nexts[index] = new TrieNode(); //新建节点 } node = node.nexts[index]; //(如果有走向a的路)节点后移 node.path++; } node.end++; //来到字符串末尾,end++ } //删除某一个字符串:沿途p--,最后一个Node的e-- //若删除中发现当前节点的下一节点p值在--之后为0,则将当前节点的下一个节点置空 public void delete(String word) { if (search(word) != 0) { //确定树中有word才进行删除操作 char[] chs = word.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (--node.nexts[index].path == 0) {//当前节点下级节点的path在--之后变为0 node.nexts[index] = null; //把下级节点置空 return; } node = node.nexts[index]; //节点后移 } node.end--; } } //查询word这个字符串加入过几次 public int search(String word) { if (word == null) { return 0; } char[] chs = word.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (node.nexts[index] == null) { return 0; //字符没结束,node结束了:例如有"abcdefg",但没有"abc" } node = node.nexts[index]; } return node.end; //字符走完,返回末尾字符节点的end值 } //查询所有加入的字符串中,有几个是以pre这个字符串作为前缀的 public int prefixNumber(String pre) { if (pre == null) { return 0; } char[] chs = pre.toCharArray(); TrieNode node = root; int index = 0; for (int i = 0; i < chs.length; i++) { index = chs[i] - 'a'; if (node.nexts[index] == null) { return 0; } node = node.nexts[index]; } return node.path; } } public static void main(String[] args) { Trie trie = new Trie(); System.out.println(trie.search("zuo")); //0 trie.insert("zuo"); System.out.println(trie.search("zuo")); //1 trie.delete("zuo"); System.out.println(trie.search("zuo")); //0 trie.insert("zuo"); trie.insert("zuo"); trie.delete("zuo"); System.out.println(trie.search("zuo")); //1 trie.delete("zuo"); System.out.println(trie.search("zuo")); //0 trie.insert("zuoa"); trie.insert("zuoac"); trie.insert("zuoab"); trie.insert("zuoad"); trie.delete("zuoa"); System.out.println(trie.search("zuoa")); //0 System.out.println(trie.prefixNumber("zuo")); //3 } }


