DiJkstra(狄克斯特拉)算法
是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。
迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
要求:图中不能有累加和为负数的环
思路:
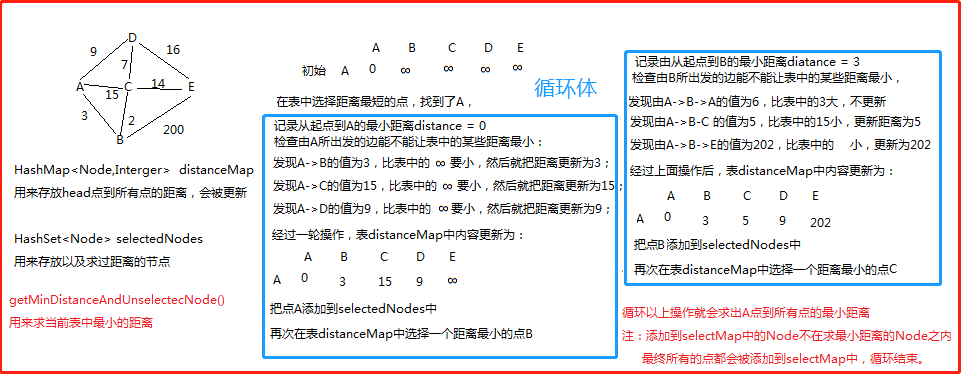
代码:
package Algorithms.Graph; import java.util.HashMap; import java.util.HashSet; import java.util.Map.Entry; public class Dijkstra { //获取从head出发到所有点的最小距离 public static HashMap<Node, Integer> dijkstra1(Node head) { //所有的距离指的是从唯一的源头(head)到当前点的最小距离 // key:从head出发到达key // value:从head出发到达key的最小距离 //如果在表中没有T的记录,含义是从head出发到T这个点的距离为正无穷 HashMap<Node, Integer> distanceMap = new HashMap<>(); distanceMap.put(head, 0);//把从head到head的最小距离0加入distanceMap中 //selectedNodes用于存放已经求过距离的节点,以后再不不碰 HashSet<Node> selectedNodes = new HashSet<>(); //得到一个距离最小的点A Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes); while (minNode != null) { int distance = distanceMap.get(minNode); //计算最小距离 for (Edge edge : minNode.edges) { //循环点A的所有边 Node toNode = edge.to; //边所对应的点X if (!distanceMap.containsKey(toNode)) { //如果点X不在distanceMap中 distanceMap.put(toNode, distance + edge.weight); //在distanceMap中记录从head到X点的距离 } else { //如果X在distanceMap中,更新最小距离 distanceMap.put(toNode, Math.min(distanceMap.get(toNode), distance + edge.weight)); } } selectedNodes.add(minNode); //把点A添加到已经求过距离的节点 //再次得到distanceMap中距离最小的节点B,然后重复以上操作, minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes); // 最后所有的点都会进入selectedNode,minNode就会为null,退出循环,返回distanceMap } return distanceMap; } //在distanceMap选择最小距离的节点,但不能是已经选过的点selectedNode public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> selectedNode) { Node minNode = null; int minDistance = Integer.MAX_VALUE; //到每点距离默认为系统最大值 for (Entry<Node, Integer> entry : distanceMap.entrySet()) { //遍历distanceMap Node node = entry.getKey(); //取当前节点 int distance = entry.getValue(); //取当前节点所对应的距离 //如果这个Node不在已经求过节点的集合中且这个距离比当前最小距离小 if (!selectedNode.contains(node) && distance < minDistance) { minNode = node; //更新最小距离的节点 minDistance = distance; //更新最小距离 } } return minNode; } }

package Algorithms.Graph; import java.util.HashMap; import java.util.HashSet; import java.util.Map.Entry; public class Dijkstra { //head到节点的最短距离 public static class NodeRecord { public Node node; public int distance; public NodeRecord(Node node, int distance) { this.node = node; this.distance = distance; } } public static class NodeHeap { private Node[] nodes; //储存节点的数组(堆的底层结构是数组) private HashMap<Node, Integer> heapIndexMap; //value:任一节点在堆上的Index。通过Node查它在不在堆上,如果在,拿到它在堆上的位置 private HashMap<Node, Integer> distanceMap; //head到Node目前最短的距离 private int size; //堆上的节点 //初始化 public NodeHeap(int size) { nodes = new Node[size]; heapIndexMap = new HashMap<>(); distanceMap = new HashMap<>(); this.size = 0; } public boolean isEmpty() { return size == 0; } //塞一条记录,如果从head出发 ,到某一个节点的记录第一次出现,增加此记录 //如果塞的记录之前有过,但这个值比记录的更小,更新此记录;如果比记录值大,忽略 public void addOrUpdateOrIgnore(Node node, int distance) { if (inHeap(node)) { //如果Node在堆上 distanceMap.put(node, Math.min(distanceMap.get(node), distance)); //更新 insertHeapify(node, heapIndexMap.get(node));//更新之后,可能经历一个往上冒的过程 } if (!isEntered(node)) { //如果Node节点没有进来过 nodes[size] = node; heapIndexMap.put(node, size); distanceMap.put(node, distance); insertHeapify(node, size++); } } //弹出一个自己定义的Node public NodeRecord pop() { NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0])); swap(0, size - 1); //把堆的最后一个元素拿到堆顶 heapIndexMap.put(nodes[size - 1], -1); //把原本的头节点指向-1位置 distanceMap.remove(nodes[size - 1]); //distanceMap中删掉此条记录 nodes[size - 1] = null; //在堆上释放size-1位置 heapify(0, --size);//试着往下移动 return nodeRecord; } private void insertHeapify(Node node, int index) { while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) { swap(index, (index - 1) / 2); index = (index - 1) / 2; } } private void heapify(int index, int size) { int left = index * 2 + 1; while (left < size) { int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left]) ? left + 1 : left; smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index; if (smallest == index) { break; } swap(smallest, index); index = smallest; left = index * 2 + 1; } } //Node进没进来过 private boolean isEntered(Node node) { return heapIndexMap.containsKey(node); } //判断一个Node在不在堆上,首先得进来过,其次Node在heapIndexMap上的位置不是-1表示在堆上 //-1表示曾经进来过,但不在堆上 private boolean inHeap(Node node) { return isEntered(node) && heapIndexMap.get(node) != -1; } private void swap(int index1, int index2) { heapIndexMap.put(nodes[index1], index2); heapIndexMap.put(nodes[index2], index1); Node tmp = nodes[index1]; nodes[index1] = nodes[index2]; nodes[index2] = tmp; } } /** * 改进后的dijkstrs算法 * 从head出发,所有head能到达的节点,生成到达每个节点的最小路径并返回 * @param head :头节点 * @param size :节点数量 * @return :HashMap<Node, Integer> Node:能够到达的节点 Interger:头节点到此节点的最短距离 */ public static HashMap<Node, Integer> dijkstra2(Node head, int size) { // NodeHeap nodeHeap = new NodeHeap(size); nodeHeap.addOrUpdateOrIgnore(head, 0); HashMap<Node, Integer> result = new HashMap<>(); while (!nodeHeap.isEmpty()) { NodeRecord record = nodeHeap.pop(); //弹出堆顶节点(小根堆) Node cur = record.node; int distance = record.distance; //找出当前节点所有的下一个节点,进行addOrUpdateOrIgnore for (Edge edge : cur.edges) { nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance); } result.put(cur, distance); //加一条记录 } return result; } }



