kruskal算法和prim算法
1、两种算法都针对无向图
2、目的:生成最小生成树
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。
一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
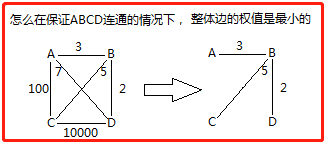
最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
一、Kruskal算法 --克鲁斯卡尔
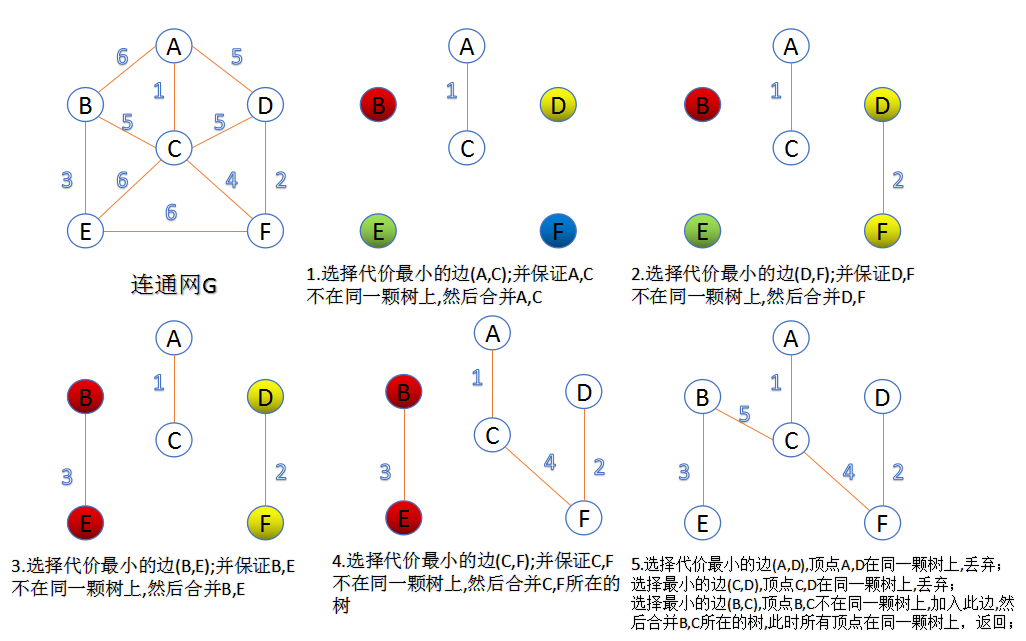
1.将图中的所有边按权值从小到大排序; 2.把图中的n个顶点看成独立的n棵树组成的森林; 3.按权值从小到大选择边,所选的边连接的两个顶点ui,vi应属于两颗不同的树,然后将这两颗树合并作为一颗树。 4.重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

package Algorithms.Graph; import java.util.*; //undirected graph only public class Kruskal { public static class Mysets{ public HashMap<Node, List<Node>> setMap; //每一个点Node都建立一个小集合,把自己放进去,然后再把(Node,{Node})放入setMap中 public Mysets(List<Node> nodes){ for (Node cur:nodes){ List<Node> set = new ArrayList<Node>(); set.add(cur); setMap.put(cur,set); } } //判断from和to两节点在不在同一集合中(比较两集合的内存地址是否相同) public boolean isSameSet(Node from,Node to){ List<Node> fromSet = setMap.get(from); List<Node> toSet = setMap.get(to); return fromSet == toSet; } //把from所在集合和to所在集合合并为一个集合 //将to集合中所有点都添加到from集合中,再把to集合中所有Node在setMap中的指向变为from所在集合 public void union(Node from,Node to){ List<Node> fromSet = setMap.get(from); List<Node> toSet = setMap.get(to); for (Node toNode:toSet ){ fromSet.add(toNode); setMap.put(toNode,fromSet); } } } //以上方法没有并查集快 //################################################################################### // Union-Find Set public static class UnionFind { private HashMap<Node, Node> fatherMap; private HashMap<Node, Integer> rankMap; public UnionFind() { fatherMap = new HashMap<Node, Node>(); rankMap = new HashMap<Node, Integer>(); } private Node findFather(Node n) { Node father = fatherMap.get(n); if (father != n) { father = findFather(father); } fatherMap.put(n, father); return father; } public void makeSets(Collection<Node> nodes) { fatherMap.clear(); rankMap.clear(); for (Node node : nodes) { fatherMap.put(node, node); rankMap.put(node, 1); } } public boolean isSameSet(Node a, Node b) { return findFather(a) == findFather(b); } public void union(Node a, Node b) { if (a == null || b == null) { return; } Node aFather = findFather(a); Node bFather = findFather(b); if (aFather != bFather) { int aFrank = rankMap.get(aFather); int bFrank = rankMap.get(bFather); if (aFrank <= bFrank) { fatherMap.put(aFather, bFather); rankMap.put(bFather, aFrank + bFrank); } else { fatherMap.put(bFather, aFather); rankMap.put(aFather, aFrank + bFrank); } } } } public static class EdgeComparator implements Comparator<Edge> { @Override public int compare(Edge o1, Edge o2) { return o1.weight - o2.weight; } } public static Set<Edge> kruskalMST(Graph graph) { UnionFind unionFind = new UnionFind(); unionFind.makeSets(graph.nodes.values()); PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator()); for (Edge edge : graph.edges) { priorityQueue.add(edge); } Set<Edge> result = new HashSet<>(); while (!priorityQueue.isEmpty()) { Edge edge = priorityQueue.poll(); if (!unionFind.isSameSet(edge.from, edge.to)) { result.add(edge); unionFind.union(edge.from, edge.to); } } return result; } }
二、prim算法 --普里姆
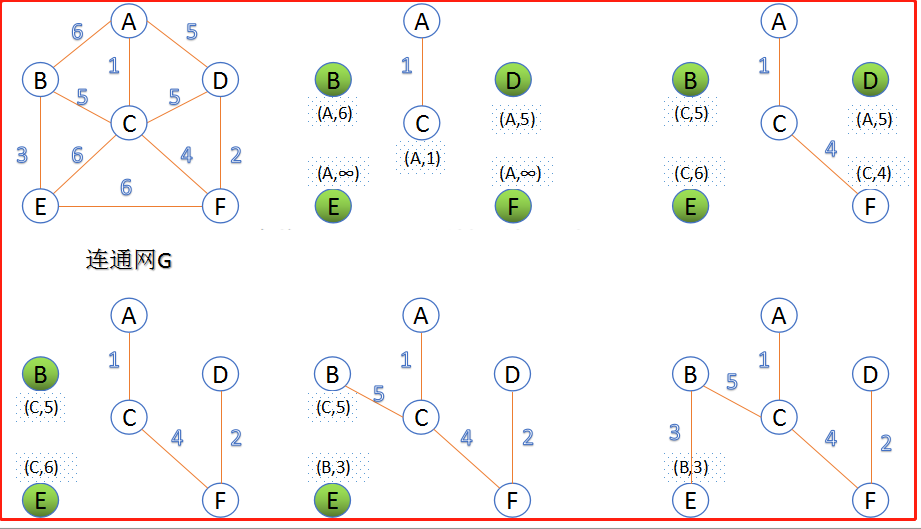
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点。
priorityQueue:优先级队列,存放解锁的边,并按照权值从小到大依次弹出解锁的边
HashSet<Node> set:把新点放入set中,用来判断一个点是否为新点
Set<Node> result:用来存放依次挑选的边
1、选择一个节点A
2、把A所有的边加入优先级队列中
3、从优先级队列中取出一个边(权值最小的边)
4、判断这个边所指向的节点是否在set集合中,如果不在,说明是一个新点,将其添加到set中
5、取出这个新点所有的边,放入优先级队列中,再重复以上步骤
代码实现
package Algorithms.Graph; import java.util.Comparator; import java.util.HashSet; import java.util.PriorityQueue; import java.util.Set; // undirected graph only public class Prim { public static class EdgeComparator implements Comparator<Edge> { @Override public int compare(Edge o1, Edge o2) { return o1.weight - o2.weight; } } public static Set<Edge> primMST(Graph graph) { PriorityQueue<Edge> priorityQueue = new PriorityQueue<>( new EdgeComparator()); //优先级队列:用来存放解锁的边 HashSet<Node> set = new HashSet<>(); Set<Edge> result = new HashSet<>(); //用来存放依次挑选的边 for (Node node : graph.nodes.values()) { //随便挑一个点,for循环是为了处理森林的问题 //node是开始点 如果一个图是连通图,就不需要for循环 if (!set.contains(node)) { set.add(node); for (Edge edge : node.edges) { //由一个点,解锁所有相连的边 priorityQueue.add(edge); //把这个点所有的边放入优先级队列中 } while (!priorityQueue.isEmpty()) { Edge edge = priorityQueue.poll(); //从优先级队列中取一个边(value值最小的边) Node toNode = edge.to; //拿到这个边所指向的Node if (!set.contains(toNode)) { // 如果这个Node不再set集合中,就是一个新Node set.add(toNode); result.add(edge); for (Edge nextEdge : toNode.edges) { //然后再把这个新Node所有的边放入优先级队列中 priorityQueue.add(nextEdge); } //以上代码可能会把重复的边扔到优先级队列中,但不影响结果(会被if条件直接跳过) } } } } return result; } // 请保证graph是连通图 // graph[i][j]表示点i到点j的距离,如果是系统最大值代表无路 // 返回值是最小连通图的路径之和 public static int prim(int[][] graph) { int size = graph.length; int[] distances = new int[size]; boolean[] visit = new boolean[size]; visit[0] = true; for (int i = 0; i < size; i++) { distances[i] = graph[0][i]; } int sum = 0; for (int i = 1; i < size; i++) { int minPath = Integer.MAX_VALUE; int minIndex = -1; for (int j = 0; j < size; j++) { if (!visit[j] && distances[j] < minPath) { minPath = distances[j]; minIndex = j; } } if (minIndex == -1) { return sum; } visit[minIndex] = true; sum += minPath; for (int j = 0; j < size; j++) { if (!visit[j] && distances[j] > graph[minIndex][j]) { distances[j] = graph[minIndex][j]; } } } return sum; } public static void main(String[] args) { System.out.println("hello world!"); } }



