如何判断一颗二叉树是完全二叉树
若设二叉树的深度为k,除第k层外,其它各层(1至k-1)的节点数都达到了最大个数,第k层所有的节点都连续几种在最左边,这就是完全二叉树
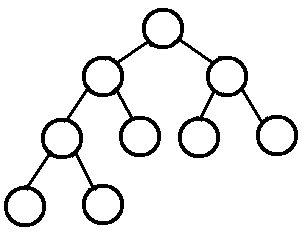
思路:按照宽度遍历进行改进
1)在遍历的过程中如果存在任何一节点有右节点,无左节点,返回false
2)在第1个条件成立的情况下,遇到了第一个左右孩子不相全的情况,则接下来遇到的所有节点都必须为叶子节点,如果是返回true,反之false
代码实现
package Algorithms.tree; import java.util.LinkedList; public class IsCBT { public static class Node { public int value; public Node left; public Node right; public Node(int data) { this.value = data; } } //判断二叉树是否为完全二叉树(二叉树宽度遍历改进而来) public static boolean isCBT(Node head) { if (head == null) { return true; } LinkedList<Node> queue = new LinkedList<>(); //是否遇到左右两个孩子不双全的节点 boolean leaf = false; Node l = null; Node r = null; queue.add(head); //1、先把头节点放入队列中 while (!queue.isEmpty()) { head = queue.poll(); // 2、poll出一个Node l = head.left; r = head.right; //poll之后由打印改为判断是否为完全二叉树 //在遇到不双全的节点后,发现当前节点不是叶子节点。或者一个节点有右节点,没有左节点,返回false if ((leaf && (l != null || r != null)) || (l == null && r != null)) { return false; } if (l != null) { //3、对于弹出的节点,把其左右节点入队列 queue.add(l); } if (r != null) { queue.add(r); } else { //如果一个节点左右孩子不双全,把leaf置true leaf = true; } } return true; } }


