求一颗二叉树的最大宽度(以及宽度遍历)
一、如何实现二叉树的宽度遍历
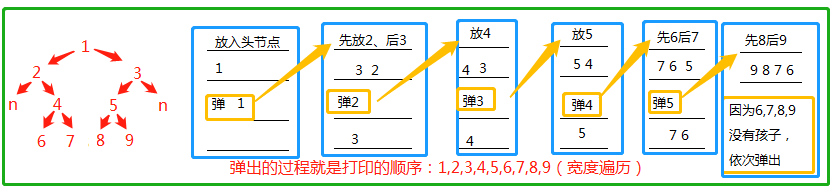
宽度遍历用队列(先进先出)
1)先把头节点放入队列中
2)每次弹出一个,打印
3)对于弹出的节点,先把弹出节点的左节点放入队列、再把其右节点放入队列(没有左右节点就不放)
重复以上三个步骤

//宽度遍历 public static void w(Node head){ if (head == null){ return; } Queue<Node> queue = new LinkedList<>(); //java中,LinkedList就是队列 queue.add(head); while(!queue.isEmpty()){ Node cur = queue.poll(); System.out.print(cur.value); if (cur.left != null){ queue.add(cur.left); } if (cur.right!= null){ queue.add(cur.right); } } }
二、求一个二叉树的最大宽度
思路,在宽度遍历的基础上进行改进:
curLevel:记录当前Node所在层数
curWidth:记录当前层的宽度
maxWidth:记录全局最大层的宽度
1、新增一个HashMap,用于记录当前Node属于哪一层
2、每次添加Node进队列时,记录当前Node所在层次
3、每次poll出一个Node时,在HashMap中获取它属于哪一层,如果属于当前层,curWidth++。反之 maxWidth = Math.max(maxWidth, curWidth) , curLevel++

//获取二叉树中最大层的宽度 public static int getMaxWidth(Node head) { if (head == null) { return 0; } Queue<Node> queue = new LinkedList<>(); //java中,LinkedList就是队列 queue.add(head); HashMap<Node, Integer> levelMap = new HashMap<>();//记录当前Node属于第几层 levelMap.put(head, 1); int curLevel = 1; //记录当前在哪一层 int curWidth = 0; //记录当前层的宽度(有几个节点),因为head进去之后没弹出,所以初始值为0 int maxWidth = -1; //记录最大层的宽度,初始值 -1 while (!queue.isEmpty()) { Node cur = queue.poll(); //弹出一个Node int curNodeLevel = levelMap.get(cur); //记录弹出的Node属于哪一层(从HahsMap中获取) //如果当前节点所遍历的层和来到的想统计的层一样, if (curNodeLevel == curLevel) { curWidth++; } else {//说明到下一层了 maxWidth = Math.max(maxWidth, curWidth); //统计当前Node之上所有层中最大层的节点数(做比较) curLevel++; //跳到下一层 curWidth = 1;//为什么是1? 比如当前节点2属于第2层(跳出第1层,不走if),走的是else // 但要统计第2层的节点数,所以初始值为1,下次再有第2层的节点被pop时,走正常的if流程 } //能够进行以上操作前提是:知道每一个Node节点所在的层数 解决办法:在进栈的时候记录它的层 if (cur.left != null) { levelMap.put(cur.left, curNodeLevel + 1);//当前Node左节点的所在层数为当前Node所在层数加1 queue.add(cur.left); } if (cur.right != null) { levelMap.put(cur.right, curNodeLevel + 1);//当前Node右节点的所在层数为当前Node所在层数加1 queue.add(cur.right); } } maxWidth = Math.max(maxWidth, curWidth); return maxWidth; }
实例代码
package Algorithms; /** * @author : zhang * @version : 1.0 * @date : Create in 2021/8/12 * @description : */ import java.util.HashMap; import java.util.LinkedList; import java.util.Queue; public class TreeMaxWidth { public static void main(String[] args) { Node head = new Node(1); head.left = new Node(2); head.right = new Node(3); head.left.left = null; head.left.right = new Node(4); head.right.left = new Node(5); head.right.right = null; head.left.right.left = new Node(6); head.left.right.right = new Node(7); head.right.left.left = new Node(8); head.right.left.right = new Node(9); //测试宽度遍历 width(head); // 1 2 3 4 5 6 7 8 9 //测试二叉树最大层的宽度 int maxWidth = getMaxWidth(head); System.out.println("二叉树最大层的宽度为:" + maxWidth); // 二叉树最大层的宽度为:4 } public static class Node { public int value; public Node left; public Node right; public Node(int data) { this.value = data; } } //宽度遍历 public static void width(Node head) { if (head == null) { return; } Queue<Node> queue = new LinkedList<>(); //java中,LinkedList就是队列 queue.add(head); while (!queue.isEmpty()) { Node cur = queue.poll(); System.out.print(cur.value + " "); if (cur.left != null) { queue.add(cur.left); } if (cur.right != null) { queue.add(cur.right); } } System.out.println(); } //获取二叉树中最大层的宽度 public static int getMaxWidth(Node head) { if (head == null) { return 0; } Queue<Node> queue = new LinkedList<>(); //java中,LinkedList就是队列 queue.add(head); HashMap<Node, Integer> levelMap = new HashMap<>();//记录当前Node属于第几层 levelMap.put(head, 1); int curLevel = 1; //记录当前在哪一层 int curWidth = 0; //记录当前层的宽度(有几个节点),因为head进去之后没弹出,所以初始值为0 int maxWidth = -1; //记录最大层的宽度,初始值 -1 while (!queue.isEmpty()) { Node cur = queue.poll(); //弹出一个Node int curNodeLevel = levelMap.get(cur); //记录弹出的Node属于哪一层(从HahsMap中获取) //如果当前节点所遍历的层和来到的想统计的层一样, if (curNodeLevel == curLevel) { curWidth++; } else {//说明到下一层了 maxWidth = Math.max(maxWidth, curWidth); //统计当前Node之上所有层中最大层的节点数(做比较) curLevel++; //跳到下一层 curWidth = 1;//为什么是1? 比如当前节点2属于第2层(跳出第1层,不走if),走的是else // 但要统计第2层的节点数,所以初始值为1,下次再有第2层的节点被pop时,走正常的if流程 } //能够进行以上操作前提是:知道每一个Node节点所在的层数 解决办法:在进栈的时候记录它的层 if (cur.left != null) { levelMap.put(cur.left, curNodeLevel + 1);//当前Node左节点的所在层数为当前Node所在层数加1 queue.add(cur.left); } if (cur.right != null) { levelMap.put(cur.right, curNodeLevel + 1);//当前Node右节点的所在层数为当前Node所在层数加1 queue.add(cur.right); } } maxWidth = Math.max(maxWidth, curWidth); return maxWidth; } //代码2 public static int getMaxWidth2(Node head) { if (head == null) { return 0; } int maxWidth = 0; int curWidth = 0; int curLevel = 0; HashMap<Node, Integer> levelMap = new HashMap<>(); levelMap.put(head, 1); LinkedList<Node> queue = new LinkedList<>(); queue.add(head); Node node = null; Node left = null; Node right = null; while (!queue.isEmpty()) { node = queue.poll(); left = node.left; right = node.right; if (left != null) { levelMap.put(left, levelMap.get(node) + 1); queue.add(left); } if (right != null) { levelMap.put(right, levelMap.get(node) + 1); queue.add(right); } if (levelMap.get(node) > curLevel) { curWidth = 0; curLevel = levelMap.get(node); } else { curWidth++; } maxWidth = Math.max(maxWidth, curWidth); } return maxWidth; } }



