相对于R-CNN、Fast RCNN的two-stage目标检测方式,即先在图像中提取候选框,再逐一对图像进行分类。候选框的生成可以是滑动窗口或选择性搜索,再对候选框进行非极大值抑制(一般只在推理时做非极大值抑制,训练时需要这些重复的框)。而YOLO则是one-stage的端到端形式:输入图片,经过深度神经网络的黑盒,得到带候选框和预测概率标注的图像。
YOLO v1
Redmon, J. "You only look once: Unified, real-time object detection." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
数据格式
对于输入的图片,划分为\(S\times S\)个grid(文中S=7),每一个grid包含2个bounding box,box的中心位于grid内,但是范围可以超出grid。bounding box的坐标和长宽由模型直接预测得到。
以数据集PASCAL VOC为例。输入图片大小为448x448x3,输出向量为7x7x30。输出向量可抽象为:\(S\times S\times(B*5+C)\)。
- SxS表示gird数量也就是49个;
- 每个grid的有\((B*5+C)\)个属性,也就是30个属性;
- 其中C表示类别数,也就是20个;
- B表示bounding box数量,也就是2个;
每个box有5个值\((x,y,w,h)\),还有置信度,\((x,y)\)表示框的中心相对于grid的边界;\(w\)宽度和\(h\)高度是相对于整个图像进行预测的;置信度预测表示预测框与任何真实框之间的IOU,在计算时,还乘以了类别的预测概率:
\[\mathrm{Pr}(\mathrm{Class}_i|\mathrm{Object})*\mathrm{Pr}(\mathrm{Object})*\mathrm{IOU}_{\mathrm{pred}}^{\mathrm{truth}}=\mathrm{Pr}(\mathrm{Class}_i)*\mathrm{IOU}_{\mathrm{pred}}^{\mathrm{truth}}
\]
训练
在训练中图像宽高被缩放到[0,1],因此每个grid内的box的x,y也被限制到[0,1]。
对最后一层使用线性激活函数,所有其他层使用Leaky ReLU:
\[\phi(x)=\begin{cases}x,&\mathrm{if~}x>0\\0.1x,&\mathrm{otherwise}&\end{cases}
\]
损失函数中,\(\mathbb{1}_{ij}^\text{obj}\)表示指示函数,第i个grid中的第j个box存在物体时,为1。否则\(\mathbb{1}_{ij}^\text{noobj}\)为1。
第1项和第2项,通过回归问题计算bounding box的\((x_i,y_i,w_i,h_i)\)与标注\((\hat{x}_i,\hat{y}_i,\hat{w}_i,\hat{h}_i)\)之间的损失。考虑到w、h较大时,允许有一定的误差;而w、h较小时,需要对误差更敏感。因此计算w、h使用了开根号。
第3项和第4项,\(C_i=\mathrm{Pr}(\mathrm{Class}_i)*\mathrm{IOU}_{\mathrm{pred}}^{\mathrm{truth}}\) 表示置信度,第3项中\(\hat{C}_i\)为ground-truth与bounding box的IoU;第4项中,\(\hat{C}_i\)为0,因为没有object。
第5项中,计算每一个grid中,所有类的概率分布\(p_i(c)\)与实际分布\(\hat{p}_i(c)\)的损失。
\[\lambda_{\mathbf{coord}}\sum_{i=0}^{S^{2}}\sum_{j=0}^{B}\mathbb{1}_{ij}^{\mathrm{obj}}\left[\left(x_{i}-\hat{x}_{i}\right)^{2}+\left(y_{i}-\hat{y}_{i}\right)^{2}\right] +
\]
\[\lambda_{\mathbf{coord}}\sum_{i=0}^{S^2}\sum_{j=0}^B1_{ij}^{\text{obj}}\left[\left(\sqrt{w_i}-\sqrt{\hat{w}_i}\right)^2+\left(\sqrt{h_i}-\sqrt{\hat{h}_i}\right)^2\right] +
\]
\[\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{obj}}\left(C_i-\hat{C}_i\right)^2 +
\]
\[\lambda_{\mathrm{noobj}}\sum_{i=0}^{S^{2}}\sum_{j=0}^{B}1_{ij}^{\mathrm{noobj}} \left(C_{i}-\hat{C}_{i}\right)^{2}+
\]
\[\sum_{i=0}^{S^{2}}\mathbb{1}_{i}^{\mathrm{obj}}\sum_{c\in\mathrm{classes}}\left(p_{i}(c)-\hat{p}_{i}(c)\right)^{2}
\]
YOLO v2
Redmon, Joseph, and Ali Farhadi. "YOLO9000: better, faster, stronger." Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.
v1缺点: mAP较低,recall较低,定位性能差,检测小目标、密集目标能力差。在模型架构和数据处理上,v2增加了以下的tricks:
- Batch Normalization:模型的每个卷积层之后、激活函数之前增加Batch Normalization。
- High Resolution Classifier,使用更高分辨率的图像预训练、训练。
- Convolutional With Anchor Boxes:v2提供了额外的先验信息,也就是anchor边框的坐标和长宽。每个grid内,有k个anchor,每个anchor各自有x,y坐标,长宽和置信度,长宽在训练前通过聚类确定。模型输出就变为\(S\times S \times \left(k\times(5+C)\right)\)
- Dimension Clusters:在训练前,对于数据集中所有边框大小进行k-means聚类,聚类指标文中使用IoU,选取k个常用的尺寸作为anchor的边框大小。
- Direct location prediction:之前的一些方法对于位置的预测方式为,模型输出偏移量\(t_w,\ t_h\)然后通过anchor的坐标\((x_a,y_a,w_a,h_a)\)计算预测框中心点的位置。
\[x=(t_x*w_a)+x_a\\y=(t_y*h_a)+y_a
\]
原论文用的是“-”,实际应为“+”。
但是在训练早期,对于预测的偏移量不加限制,往往使得训练不稳定,例如\(t_x=1\),\(t_x=-1\)会导致预测的位置和anchor的位置几乎不重合。因此,作者对于偏移量x,y坐标,长、宽以及预测置信度\(t_x,t_y,t_w,t_h,t_o\)进行了限制:
\[\begin{aligned}
b_{x}& =\sigma(t_x)+c_x \\
b_{y}& =\sigma(t_y)+c_y \\
b_{w}& =p_we^{t_w} \\
b_{h}& =p_he^{t_h} \\
Pr(\text{object})*IOU(b,\text{object})& =\sigma(t_o) = b_o
\end{aligned}\]
其中,\(\sigma\)表示sigmoid函数,\(p_w,p_h\)表示给定的anchor边框的长宽,\((c_x,c_y)\)表示归一化后,grid左上角的坐标。
- Fine-Grained Features:类似于resnet的残差连接,把中间结果进行投影与输入(指的是输入中间层的输入)做一个concatenate,结果得到了1%的提升。
- Multi-Scale Training:由于v2使用的网络架构上,没有线性层而是用1x1的卷积代替了,因此对于输入不再需要固定大小,也能更好地适用于不同大小的图像。使用的基准模型为Darknet-19:
\[\begin{array}{|c|c|c|c|}
\hline
\textbf{Type} & \textbf{Filters} & \textbf{Size/Stride} & \textbf{Output} \\
\hline
\text{Convolutional} & 32 & 3 \times 3 & 224 \times 224 \\
\text{Maxpool} & - & 2 \times 2 / 2 & 112 \times 112 \\
\text{Convolutional} & 64 & 3 \times 3 & 112 \times 112 \\
\text{Maxpool} & - & 2 \times 2 / 2 & 56 \times 56 \\
\text{Convolutional} & 128 & 3 \times 3 & 56 \times 56 \\
\text{Convolutional} & 64 & 1 \times 1 & 56 \times 56 \\
\text{Convolutional} & 128 & 3 \times 3 & 56 \times 56 \\
\text{Maxpool} & - & 2 \times 2 / 2 & 28 \times 28 \\
\text{Convolutional} & 256 & 3 \times 3 & 28 \times 28 \\
\text{Convolutional} & 128 & 1 \times 1 & 28 \times 28 \\
\text{Convolutional} & 256 & 3 \times 3 & 28 \times 28 \\
\text{Maxpool} & - & 2 \times 2 / 2 & 14 \times 14 \\
\text{Convolutional} & 512 & 3 \times 3 & 14 \times 14 \\
\text{Convolutional} & 256 & 1 \times 1 & 14 \times 14 \\
\text{Convolutional} & 512 & 3 \times 3 & 14 \times 14 \\
\text{Convolutional} & 256 & 1 \times 1 & 14 \times 14 \\
\text{Convolutional} & 512 & 3 \times 3 & 14 \times 14 \\
\text{Maxpool} & - & 2 \times 2 / 2 & 7 \times 7 \\
\text{Convolutional} & 1024 & 3 \times 3 & 7 \times 7 \\
\text{Convolutional} & 512 & 1 \times 1 & 7 \times 7 \\
\text{Convolutional} & 1024 & 3 \times 3 & 7 \times 7 \\
\text{Convolutional} & 512 & 1 \times 1 & 7 \times 7 \\
\text{Convolutional} & 1024 & 3 \times 3 & 7 \times 7 \\
\text{Convolutional} & 1000 & 1 \times 1 & 7 \times 7 \\
\text{Avgpool} & - & \text{Global} & 1000 \\
\text{Softmax} & - & - & - \\
\hline
\end{array}
\]
每一轮迭代的损失:
\[\begin{aligned}
loss_{t}=\sum_{i=0}^{W}\sum_{j=0}^{H}\sum_{k=0}^{A}&\mathbb{1}_\text{max(IOU)<Thresh}\lambda_{noobj}*\left(-b_{ijk}^{o}\right)^{2} \\
&+\mathbb{1}_{t<12800} \lambda_{prior}*\sum_{r\in(x,y,w,h)}\bigl(prior_{k}^{r} - b_{ijk}^{r}\bigr)^{2} \\
&+\mathbb{1}_{k}^{truth}( \lambda_{coord} *\sum_{r \epsilon (x,y,w,h)}(truth^{r} - b_{ijk}^{r})^{2} \\
&+\lambda_{obj}*\left(IOU_{truth}^{k}-b_{ijk}^{o}\right)^{2} \\
&+\lambda_{class} *(\sum_{c=1}^{C}(truth^{c} - b_{ijk}^{c})^{2}) )
\end{aligned}\]
相较于v1的损失函数设置,v2在训练的前几个迭代中,会鼓励模型预测的bounding box与anchor的边框一致,后面训练稳定下来后,便不再计算与anchor有关的损失了。回归的数据不再直接是坐标和长宽,而是相对于anchor的偏移量。
YOLO v3
Farhadi, Ali, and Joseph Redmon. "Yolov3: An incremental improvement." Computer vision and pattern recognition. Vol. 1804. Berlin/Heidelberg, Germany: Springer, 2018.
v3的损失:
\[\lambda_{coord}{\sum_{i=0}^{S^2}\sum_{j=0}^{B}\mathbb{1}_{i,j}^{obj}}\cdot[(b_x-\hat{b}_x)^2+(b_y-\hat{b}_y)^2+(b_w-\hat{b}_w)^2+(b_h-\hat{b}_h)^2]
\]
\[+\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{i,j}^{obj}\cdot[-\log(p_c)+\sum_{i=1}^nBCE(\hat{c_i},c_i)]
\]
\[+\lambda_{noobj}{\sum_{i=0}^{S^2}\sum_{j=0}^{B}}\mathbb{1}_{ij}^{noobj}[-\log(1-p_c)]
\]
- Bounding Box Prediction:在损失第1项,与v2一样,v3会通过逻辑回归计算每个anchor box的\((b_x,b_y,b_w,b_h)\),但是只会计算1个anchor box的回归损失,也就是与ground truth的IOU最大的那个anchor box(它就是正样本\(\mathbb{1}_{i,j}^{obj}=1\)),其他的anchor box,如果它的IOU大于某个阈值(默认0.5),就忽略它。如果小于阈值且没有被分配ground truth,我们就把它当作负样本\(\mathbb{1}_{ij}^{noobj}=1\),只有计算损失第3项的时候才去用。
\[\begin{aligned}
b_{x}& =\sigma(t_x)+c_x \\
b_{y}& =\sigma(t_y)+c_y \\
b_{w}& =p_we^{t_w} \\
b_{h}& =p_he^{t_h}
\end{aligned}\]
-
Class Prediction:在损失第2项,对于输出logits,不再使用softmax,而是逻辑回归(如sigmoid)。损失函数自然也变成二元交叉熵损失,分别计算每个类的损失,这保证了同时存在多个类的情况。
-
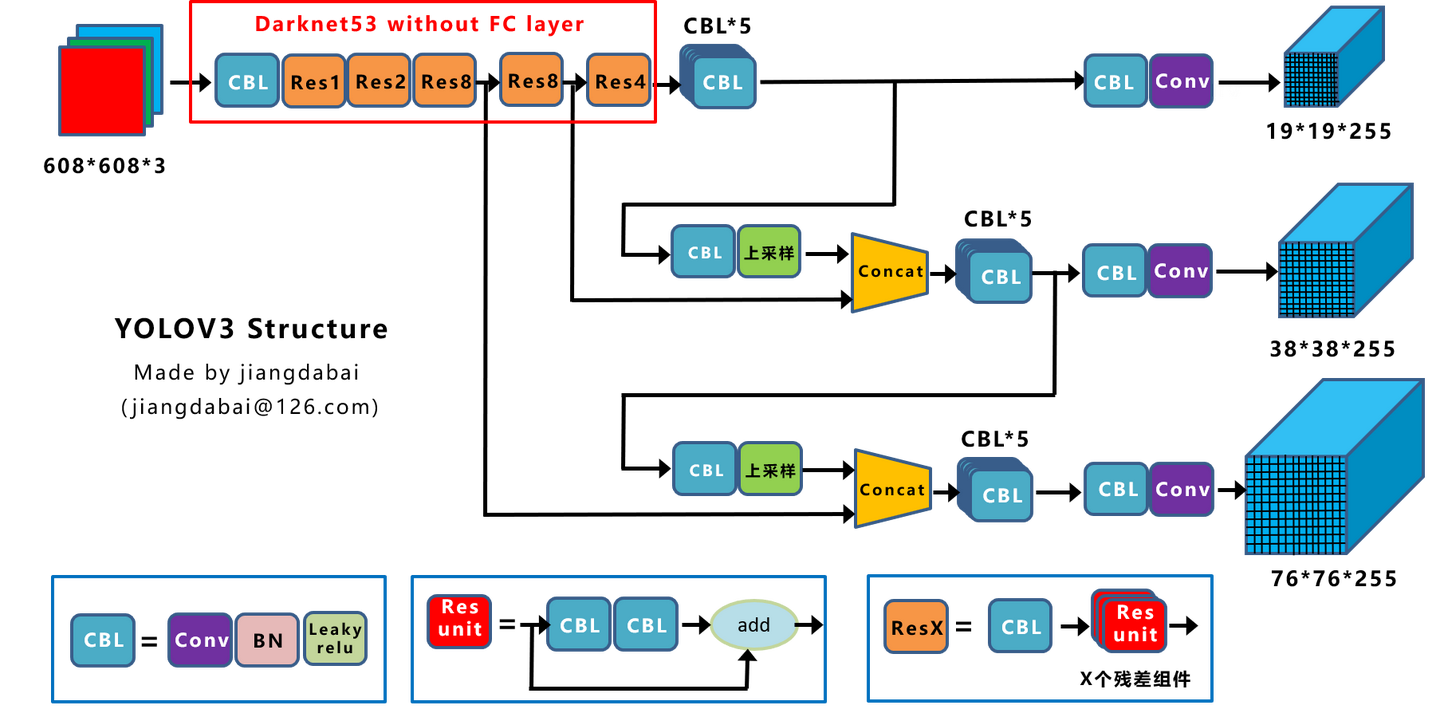
Predictions Across Scales:v3的模型能输出三种尺度的特征,在COCO中,有80个类,输出3个\(N\times N\times[3*(4+1+80)]\)的特征,N表示每个尺度的grid数量,3表示每个grid的anchor box数量,4表示bounding box的坐标和长宽,1表示置信度,80表示类别。
参考下图,随着网络越来越深,中间结果的尺度越来越小。大尺度的特征一部分来自小尺度特征的上采样;一部分来自较靠前的中间层结果。两者concatenate得到。
由于有3种尺度,因此anchor box的大小有3 x 3种,同样通过聚类得到。v3的backbone选择为Darknet-53。