[CVPR2024]CDMAD Class-Distribution-Mismatch-Aware Debiasing for Class-Imbalanced Semi-Supervised Learning
在不平衡半监督学习的设置下,分类器往往会偏向头部类,这种偏置在有标签集合和无标签集合分布不一致的情况下会进一步加剧,也更难生成准确的伪标签。文中提出了一种新的简单的衡量分类器偏好程度的方法:通过分类器对无意义图片的预测结果来度量模型对类别的偏好,同时根据偏好,在伪标签生成阶段和分类测试阶段调整分类器输出。
Introduction
在不平衡数据集上训练的分类器往往对头部类(majority classes)有偏好。在半监督学习(semi-supervised learning,SSL) 设置下,生成伪标签的算法由于生成带偏置的伪标签,往往会进一步加剧偏置。带偏置的伪标签会降低表征学习质量。特别的,如果有标签集合和无标签集合的分布差异大,偏置将会变得更严重。
一部分不平衡SSL算法假设labeled set和unlabeled set分布一致,然而这种做法并不现实,例如数据集STL-10搜集了不同时期样本,导致类别分布不一致。一些算法,在主要的训练阶段不假设这种一致性,但在主要训练结束后使用额外的用于全监督不平衡学习的技术,如classifier retrain(cRT)和 logit-adjustment(LA)。
cRT仅使用了labeled set数据而无标签数据不参与其中。LA由于没有考虑无标签数据的分布,当labeled set与unlabeled set分布不一致时,不能很好的实现重平衡。
Motivation
不平衡半监督学习相关的论文都是提出一些组件,如新的分类器、调整logit,与一些经典的半监督学习框架结合。文中,作者为了让半监督框架更契合不平衡数据集,做出了改进。
- FixMatch中,对于弱增强的预测标签,筛选阈值大于\(\tau\)的部分,选取预测值最大的类作为伪标签。

- ReMixMatch对于伪标签生成增加了标签对齐操作:\(\tilde{q_b}=Normalize\left(q_b\times P_l\left(y\right)/q\left(y\right)\right)\)。其中\(q_b\)表示软标签,\(P_l\left(y\right)\)表示labeled set类别分布。\(q(y)\)表示前128个预测标签移动平均(moving average),Normalize表示标准化,然后再对对齐的伪标签锐化:\(\bar{q_b}=Normalize\left(\tilde{q_b}^{1/T}\right)\)。在文中,对于无标签数据分布未知的情况下不再使用分布对其。因为考虑到有标签/无标签数据分布不同的情况,这样可以防止低质量的伪标签的生成。
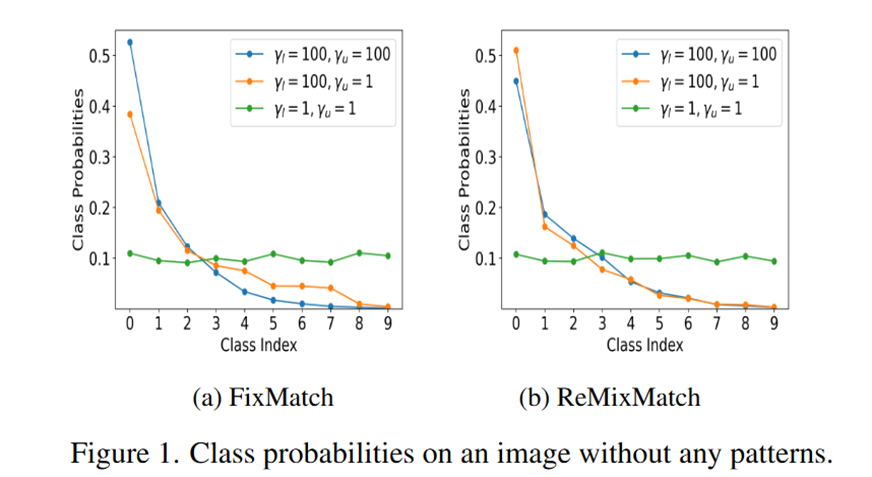
可以合理假设纯色图片不含任何被模型学习的特征。因此对它的预测偏置也反映了分类器的偏置。
Method
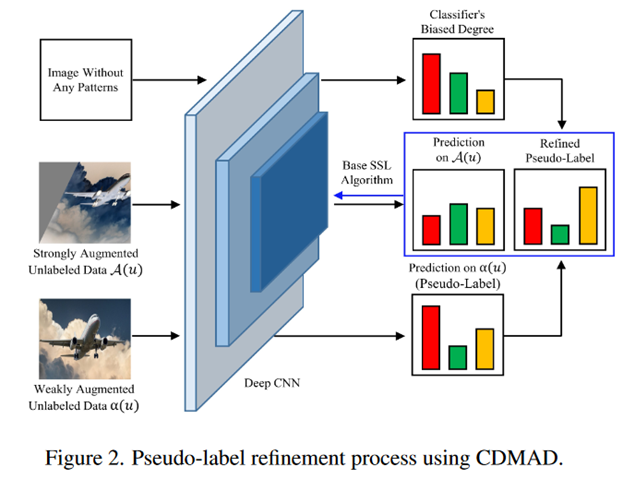
方法部分非常简单,使用\(g_\theta\left(\mathcal{I}\right)\)表示纯色图片的logits,一共在两个用到了它:
-
训练阶段
训练时的伪标签生成阶段:对于弱增强的预测logits:\(g_\theta\left(\alpha\left(u_b^m\right)\right)\)减去偏置:\(g_\theta^*\left(\alpha\left(u_b^m\right)\right)=g_\theta\left(\alpha\left(u_b^m\right)\right)-g_\theta\left(\mathcal{I}\right)\),再softmax得到伪标签:\(q_b^*=\phi\left(g_\theta^*\left(\alpha\left(u_b^m\right)\right)\right)\) -
测试阶段
测试时的logit调整阶段:\(g_\theta^*\left(x_k^{test}\right)=g_\theta\left(x_k^{test}\right)-g_\theta\left(\mathcal{I}\right)\),得到最后的标签\(f_\theta^*\left(x_k^{test}\right)=\arg\max_cg_\theta^*\left(x_k^{test}\right)_c\)。这里作者和logits adjustment方法\(g_\theta^*\left(x_k^{test}\right)=g_\theta\left(x_k^{test}\right)-\log\pi\)进行了比较,可以看作是LA的扩展:\(g_\theta\left(\mathcal{I}\right)+constant = \log P_\theta\left(y|\mathcal{I}\right)\)。因此符合Fisher一致性,可以最小化平衡误差。
在实验部分,作者把用到的纯白图片替换为其他分布(Uniform、Bernoulli、Normal)随机生成、和其他颜色的图片,以及非图片(值在[0,255]之外的矩阵),比较。结果性能比较:非图片>白色>其他颜色>其他分布。
参考文献
- Sohn, Kihyuk, et al. "Fixmatch: Simplifying semi-supervised learning with consistency and confidence." Advances in neural information processing systems 33 (2020): 596-608.
- David Berthelot, Nicholas Carlini, Ekin D Cubuk, Alex Kurakin, Kihyuk Sohn, Han Zhang, and Colin Raffel. Remixmatch: Semi-supervised learning with distribution matching and augmentation anchoring. In International Conference on Learning Representations, 2020.
- Lee, Hyuck, and Heeyoung Kim. "CDMAD: Class-Distribution-Mismatch-Aware Debiasing for Class-Imbalanced Semi-Supervised Learning." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2024.



