[AAAI2024]Out-of-Distribution Detection in Long-Tailed Recognition with Calibrated Outlier Class Learning

这篇文章设置的问题是：考虑长尾分布的训练集下，对测试集上的OOD样本进行检测。作者在训练集中引入了open set样本学习异常表征，以OCL（Outlier Class Learn）为baseline，训练时引入prototype方法，推理时对logits进行调整校准。

问题背景

DNNs会把OOD（out-of-distribution）样本误分类为ID（in-distribution）样本，训练集为长尾分布时，问题被进一步加剧，表现为：

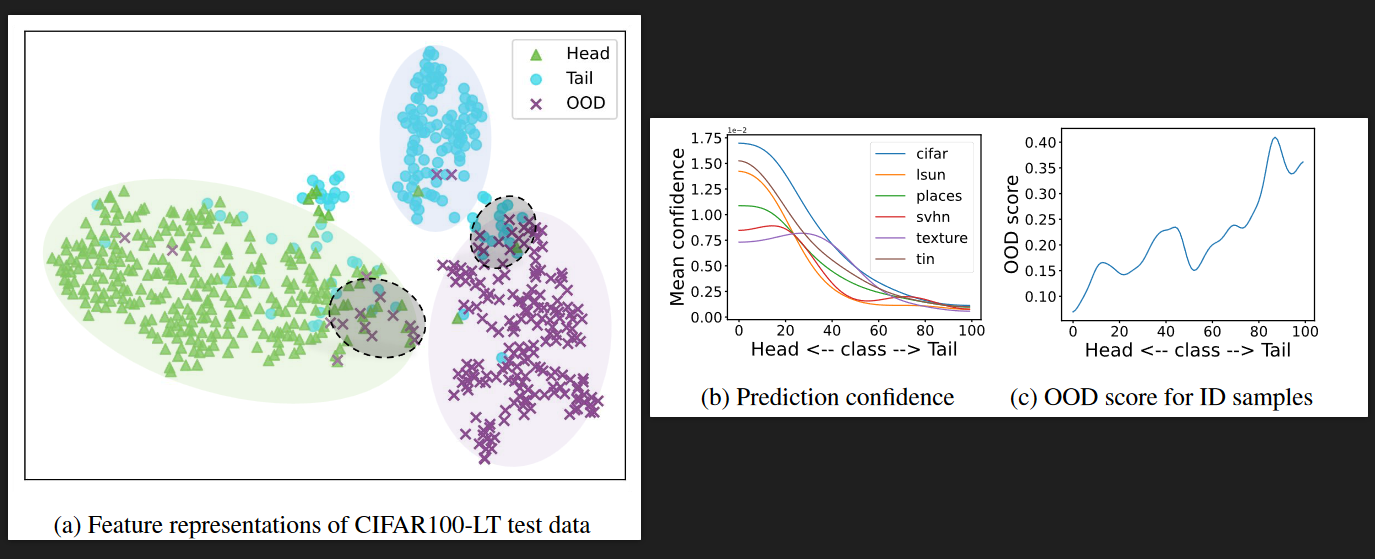
• OOD样本以较高的置信度分为head classes。
• tail classes样本比head classes样本更容易被误分类为OOD样本。

Related Work

平衡数据集下的OOD检测

1. 事后方法（post hoc methods）：在推理阶段，设计新的OOD打分函数。
2. 使用辅助的open set数据集，最早由[2]提出的OE（outlier exposure）损失函数，对于open set样本使用单独的损失函数。这里\(u\)表示基于均匀分布的OOD数据伪标签，与[3]中对于引入的open set打标签做法相似，详见此处。

\[\mathcal{L}_{OE}=\mathbb{E}_{x,y\sim\mathcal{D}_{in}}[\ell(f(x),y]+\gamma\mathbb{E}_{x\sim\mathcal{D}_{out}}[\ell(f(x),u],\tag{1} \]

长尾学习下的OOD检测

1. 使用辅助的open set数据集使得模型对OOD检测更robust，[3]的问题设置主要针对长尾学习，但在实验中也提到了OOD检测。
2. 将OOD的预测概率拟合进长尾分布，但在长尾学习中很难获取准确的OOD分布。因此作者使用OCL（outlier class learning）作为baseline。这里\(\tilde{y}=k+1\)，k表示ID类的数量。

\[\mathcal{L}_{OCL}=\mathbb{E}_{x,y\sim\mathcal{D}_{in}}[\ell(f(x),y]+\gamma\mathbb{E}_{x\sim\mathcal{D}_{out}}[\ell(f(x),\tilde{y}], \tag{2} \]

作者在实验中发现，一般的OOD检测任务中，OE表现优于OCL，但在长尾学习下，OCL表现优于OE。这是因为设置open set样本的先验概率为均匀分布，在长尾设置下并不合理。因此选用OCL为baseline。但需要考虑两个问题：OOD被误分类head classes；tail classes样本更容易被误分类为OOD。

Method

整体的框架如图所示，在训练阶段引入Debiased large margin learning，推理阶段引入Outlier-class-aware logit calibration。

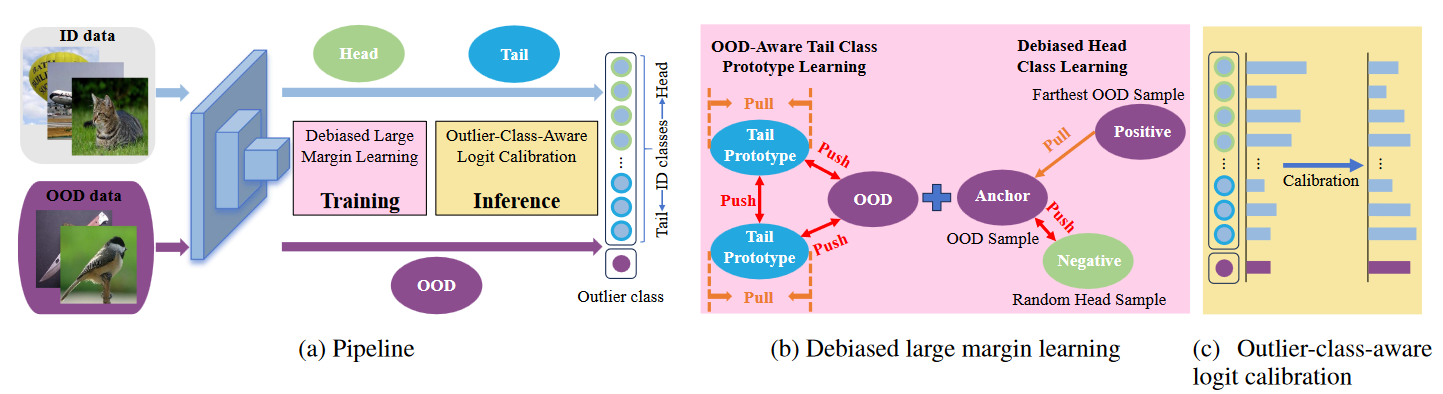
训练阶段的Debiased large margin learning

解决“tail classes样本更容易被误分类为OOD”：

之前的工作利用各种增强将尾部样本推离OOD样本，但由于尾部类别的大小有限，学习不到两者间区分明显的表征。

为了解决这个问题，作者使用一个可学习的prototype代表一个tail class，同类的样本拉近prototype，并推离其他尾部类prototype和OOD样本，利用尾部原型来增加尾部类表示的存在，有助于减少模型对OOD样本的偏差。原型表示为\(\mathcal{M}\in\mathbb{R}^{N\times D}\)。N表示可学习参数数量，D表示特征维度，优化目标为：

\[\mathcal{L}_t=\mathbb{E}_{x\sim\mathcal{D}_{tail}}[\mathcal{L}_t(x,\mathcal{M})],\tag{3} \]

\[\mathcal{L}_t(x,\mathcal{M})=\frac1{|\mathcal{B}|}\sum_{x\in\mathcal{B}}log\frac{exp(z(x)m_x^\intercal/t)}{\sum_{m\in\mathcal{M}}exp(z(x)m^\intercal/t)+P(x)},\tag{4} \]

这里P与batch内的开集样本相关，\(P(x)=\sum_{\hat{x}\in\mathcal{O}}exp(z(x)z(\hat{x})^\intercal/t)\)；m表示为\(\mathcal{M}\)内的尾部类原型，z表示为logits，t表示为温度参数。

形式上，与moco的损失函数相同：\(\mathcal{L}_q=-\log\frac{\exp(q\cdot k_+/\tau)}{\sum_{i=0}^K\exp(q\cdot k_i/\tau)}\)。

解决“OOD被误分类head classes”：

由于长尾数据集中，head classes样本数量极大，OOD样本很容易被归类为head classes。此处，作者引入了对比学习：选择1个OOD样本为anchor，随机挑选一个head classes样本为negative samples（\(x^n\)）和另一个OOD样本为positive samples（\(x^p\)），优化目标为：

\[\mathcal{L}_h=\mathbb{E}_{x\sim\mathcal{D}_{out}}[\mathcal{L}_h(x)], \]

\[\mathcal{L}_{h}(x)=\frac1{|\mathcal{B}|}\sum_{x\in\mathcal{B}}max(0,\|z(x)-z(x^p)\|_2^2-\|z(x)-z(x^n)\|_2^2+margin), \]

其中margin为超参数，最后的损失函数定义为：

\[\begin{aligned} \mathcal{L}_{total}& =\mathcal{L}_{OCL}+\alpha\mathcal{L}_t+\beta\mathcal{L}_h \\ &=\mathbb{E}_{x,y\thicksim\mathcal{D}_{in}}[\ell(f(x),y]+\gamma\mathbb{E}_{x\thicksim\mathcal{D}_{out}}[\ell(f(x),\tilde{y}] \\ &+\alpha\mathbb{E}_{x\sim\mathcal{D}_{tail}}[\mathcal{L}_{t}(x,\mathcal{M})]+\beta\mathbb{E}_{x\sim\mathcal{D}_{out}}[\mathcal{L}_{h}(x)], \end{aligned}\]

推理阶段的Outlier-class-aware logit calibration

推理阶段时，head classes样本比tail classes和OOD有着更高的预测置信度，为了解决这个问题（尽可能得多筛选出OOD样本），作者提出了Outlier-class-aware logit calibration：

\[P(y=i|x)=\frac{e^{f_i(x)-\tau\cdot\log n_i}}{\sum_{j=1}^{k+1}e^{f_j(x)-\tau\cdot\log n_j}}, \]

其中\(n_i\)为闭集类的样本数占闭集类总样本数：\(n_i=\frac{N_i}{N_1+N_2+\cdots+N_k}\)，对于异常类k+1类，认为ID分类和OOD检测同样重要，因此设置为\(n_{k+1}=1\)。这样，降低头类概率，增加尾类概率，同时考虑OOD样本对预测的影响。

实验设置

训练集加入了open set样本，但加入的open set样本与测试集的OOD样本无交集。以cifar10为例，训练集的opens set辅助数据集为TinyImages 80M；测试集的OOD数据集分别加入数据集Texture、SVHN、CIFAR100、Tiny ImageNet、LSUN、Place365，并分别做测试，统计AUC、AP-in、AP-out、FPR，也就是测试了6次，如果测试集加入的OOD类与训练集样本的类有重合，需要把它剔除。

参考文献

1. Miao, Wenjun, et al. "Out-of-distribution detection in long-tailed recognition with calibrated outlier class learning." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 38. No. 5. 2024.
2. Hendrycks, Dan, Mantas Mazeika, and Thomas Dietterich. "Deep Anomaly Detection with Outlier Exposure." International Conference on Learning Representations. 2018.
3. Wei, Hongxin, et al. "Open-sampling: Exploring out-of-distribution data for re-balancing long-tailed datasets." International Conference on Machine Learning. PMLR, 2022.