[ICML2022]Open-Sampling Exploring Out-of-Distribution Data for Re-balancing Long-tailed Datasets

在长尾数据中，作者主动加入开集噪声，并按一定比例赋予噪声样本闭集标签，来帮助长尾学习。

引入开集样本训练模型有点像dropout，“破坏”某些模型参数防止尾部类的过拟合

Motivation

长尾学习中的训练数据集分布不平衡的问题，解决方法之一是重采样。重采样主要对于尾部类重复采用，但这种做法往往会导致尾部类的过拟合。

为了缓解过拟合[2]（Rethinking the value of labels for improving class-imbalanced learning）引入了无标签的闭集类样本（闭集类指数据的label属于训练集label），再用半监督的方式对于无标签附加伪标签。但还是需要较多成本收集闭集样本。

这篇论文作者受此启发，希望引入开集样本平衡长尾数据集。作者先基于一个理论：均匀得为开集样本赋予闭集噪声标签，即开集样本有1/K概率成为j类（K为闭集类种类，j为任意一个闭集类），不会影响分类器。从贝叶斯定理的角度证明如下：

根据贝叶斯定理：\(\mathrm y^*=\arg\max_{y\in\mathcal{Y}}P(y|x)=\arg\max_{y\in\mathcal{Y}}P(x|y)P(y),\)

假设：\(\arg\max_{y\in\mathcal{Y}}P_{\mathrm{mix}}(\boldsymbol{x}|y)P_{\mathrm{mix}}(y)=\arg\max_{y\in\mathcal{Y}}P_{\mathrm{s}}(\boldsymbol{x}|y)P_{\mathrm{s}}(y).\)

\(P_\mathbf{s}\)表示训练集，样本数为N；\(P_\mathbf{out}\)表示开集数据集，样本数为M，它的标签为均匀分配的噪声标签；\(P_\mathbf{mix}\)为两者混合的数据集。

\[\begin{aligned} &P_{\mathrm{mix}}(x|y)P_{\mathrm{mix}}(y) \\ &\text{=} \frac{N}{M+N}P_{\mathrm{s}}(\boldsymbol{x}|y)P_{\mathrm{s}}(y)+\frac{M}{M+N}P_{\mathrm{out}}(\boldsymbol{x}|y)P_{\mathrm{out}}(y) \\ &\text{=} \frac{N}{M+N}P_{\mathrm{s}}(\boldsymbol{x}|y)P_{\mathrm{s}}(y)+\frac{M}{M+N}P_{\mathrm{out}}(\boldsymbol{x})P_{\mathrm{out}}(y) \\ &\text{=} \frac{N}{M+N}P_{\mathrm{s}}(\boldsymbol{x}|y)P_{\mathrm{s}}(y)\quad+\frac{1}{K}\cdot\frac{M}{M+N}P_{\mathrm{out}}(\boldsymbol{x}), \end{aligned} \]

简单来说，由于\(P_\mathbf{out}\)标签均匀赋予，因此先验\(P_\mathbf{out}(y)\)为常数1/K。

\[\begin{aligned} &\arg\max_{y\in\mathcal{Y}}P_{\mathrm{mix}}(\boldsymbol{x}|y)P_{\mathrm{mix}}(y) \\ &\text{=} \arg\operatorname*{max}_{y\in\mathcal{Y}}\left\{\frac{N}{M+N}P_{\mathrm{s}}(x|y)P_{\mathrm{s}}(x,y)+\frac{M/K}{M+N}P_{\mathrm{out}}(x)\right\} \\ &\text{=} \arg\max_{y\in\mathcal{Y}}\frac{N}{M+N}P_{\mathrm{s}}(\boldsymbol{x}|y)P_{\mathrm{s}}(\boldsymbol{x},y). \\ &\text{=} \underset{y\in\mathcal{Y}}{\operatorname*{\arg\max}}P_{\mathbf{s}}(x|y)P_{\mathbf{s}}(x,y). \end{aligned} \]

最后的预测结果取最大值，常数部分可忽略，因此混合数据集和原来的闭集数据集上的贝叶斯预测结果相同。

Method

开集样本标签的分配

均匀加入开集噪声后的\(P_\mathbf{mix}\)依然是不平衡的，但如果简单的把开集样本label赋予尾部类“9”会导致性能下降。

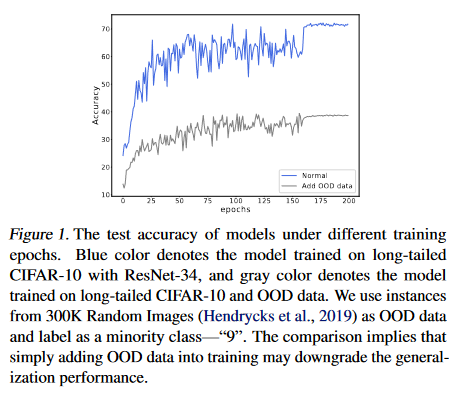
为了保持开集噪声样本不会降低性能，且平衡长尾数据集，作者提出补偿分布（Complementary Distribution），用于衡量开集样本上各个标签的分布，表示为\(\Gamma\)。引入尽可能少的开集样本的补偿分布称为Minimum Complementary Distribution (MCD)，表示为\(\Gamma^m\)，其实两者可以当成一回事。

补偿采样率（Complementary Sampling Rate）：每个开集样本被赋予标签j的概率：\(\Gamma_j=\frac{\alpha-\beta_j}{K\cdot\alpha-1},\ \beta_j=\frac{n_j}{\sum^K_{i=1}n_i}\)，不难看出补偿采样率：

• \(\sum_{i=1}^K\Gamma_i=1\)
• \(\lim_{\alpha\to\infty}\Gamma_j=\frac{1}{K}\)

以及定义\(\Gamma=\Gamma^{m}, \alpha=\max(\beta_j)\)，此时开集样本不会被赋予j=0类标签。

整体训练伪代码如下，值得注意的是，每一个epoch都会重新赋予开集样本噪声标签。

引入对应的损失函数正则化项

为了防止开集噪声占用太多模型参数，导致无法收敛，特别是M>>N时，提出了正则化项专门处理开集噪声样本：

\[\mathcal{L}_{\mathrm{reg}}=\mathbb{E}_{\widetilde{\boldsymbol{x}}\sim P_{\mathrm{out}}(X)}\left[\omega_{\widetilde{y}}\cdot\ell\left(f(\widetilde{\boldsymbol{x}};\boldsymbol{\theta}),\widetilde{y}\right)\right] \]

\(\omega_{\widetilde{y}}\)为对应类的损失权重\(\omega_{\widetilde{y}}=\Gamma_{\widetilde{y}}\cdot K.\)，标签$\widetilde{y}\sim\Gamma $。原来的闭集样本使用自身标签训练，整体的损失函数为：

\[\begin{aligned}\mathcal{L}_{\mathrm{total}}&=\mathbb{E}_{((\boldsymbol{x},y)\thicksim P_\mathrm{s}(X,Y))}\left[\ell\left(f(\boldsymbol{x};\boldsymbol{\theta}),y\right)\right]\\&+\eta\cdot\mathbb{E}_{(\widetilde{\boldsymbol{x}})\thicksim P_{\mathrm{out}}(X)}\left[\omega_{\widetilde{y}}\cdot\ell\left(f(\widetilde{\boldsymbol{x}};\boldsymbol{\theta}),\widetilde{y}\right)\right],\end{aligned} \]

上式可简写，其中\(\mathcal{L}_{\mathrm{imb}}\)可替换为其他基于损失函数的方法：

\[\mathcal{L}_{\mathrm{total}}=\mathcal{L}_{\mathrm{imb}}+\eta\cdot\mathcal{L}_{\mathrm{reg}}. \]

Experiments

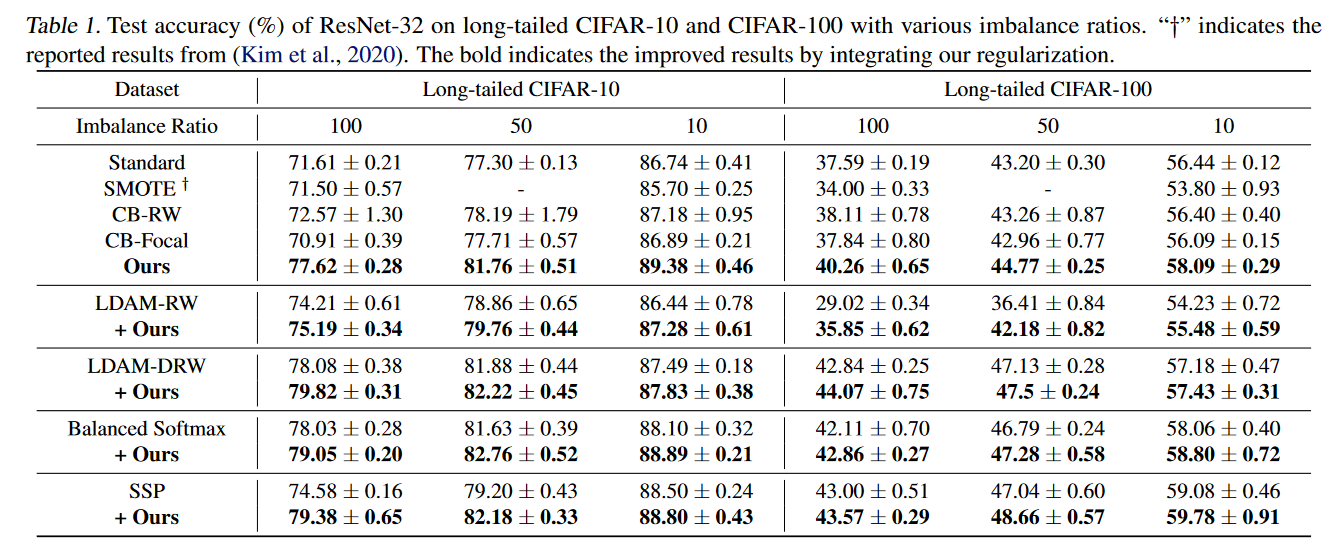
open-sampling（作者的方法）和不同的sample策略，以及附加在baseline上的提高的比较：

作者还测试了测试集上的OOD检测性能；超参\(\alpha,\ \eta\)的设置；测试了开集样本数据集的选择对性能表现有影响；开集样本的多样性对性能没有太大影响；用t-sne可视化表征分布，表明引入开集样本能促进表征学习

参考文献

1. Wei, Hongxin, et al. "Open-sampling: Exploring out-of-distribution data for re-balancing long-tailed datasets." International Conference on Machine Learning. PMLR, 2022.
2. Yang, Yuzhe, and Zhi Xu. "Rethinking the value of labels for improving class-imbalanced learning." Advances in neural information processing systems 33 (2020): 19290-19301.