f-VAEGAN-D2：VAE+GAN处理零样本学习问题

虽然f-VAEGAN-D2在题目中说“适用任意样本”，但对比的Few-shot相关的实验较少，这里仅讨论零样本学习的情况。

1. 背景介绍

由于为每个对象收集足够数量的高质量带标签样本难以实现，使用有限的标签进行训练学习一直是一个重要的研究方向。零样本学习（Zero-Shot Learning, ZSL）最初被称为计算机视觉中的零数据学习，目标是在标签受到极大限制的设置下，完成训练。在传统的ZSL中（或称为归纳零样本学习），没有为目标类提供训练示例，因此这些类被称为未见类。对于训练示例，是有着标签配对的大量训练样本，这些样本的类被称为可见类。传统零样本学习的核心挑战是：对于存在的相关知识，使分类器能够从可见类中提取的知识转移到未见类中。类别相关的信息一般以辅助信息的形式给出，作为可见类与未见类知识迁移的桥梁，辅助信息被编码为嵌入向量后使用，辅助信息可以是由人工标注的属性信息、文本描述、知识图谱或本体(Ontology)等。

对于未见类，仅使用辅助信息学习会导致未见类真实分布与建模分布之间存在差异，这被称为域转移问题。为了简化零样本学习，提出了转导零样本学习（Transductive Zero-Shot Learning, TZSL），它允许在训练中额外包含未见类的未标记样本。

在足够的数据样本示例支持下，使用生成模型学习数据点的概率分布，以便从中采样并合成示例,实现数据增强，帮助TZSL学习未见类的数据分布。

2. 方法

f-VAEGAN-D2

GAN在训练时容易遭受模型坍塌问题，而VAE对于特征的生成更加稳定，f-VAEGAN-D2作者结合两者优点通过消融实验证明将VAE与GAN结合能更好地生成图像特征。

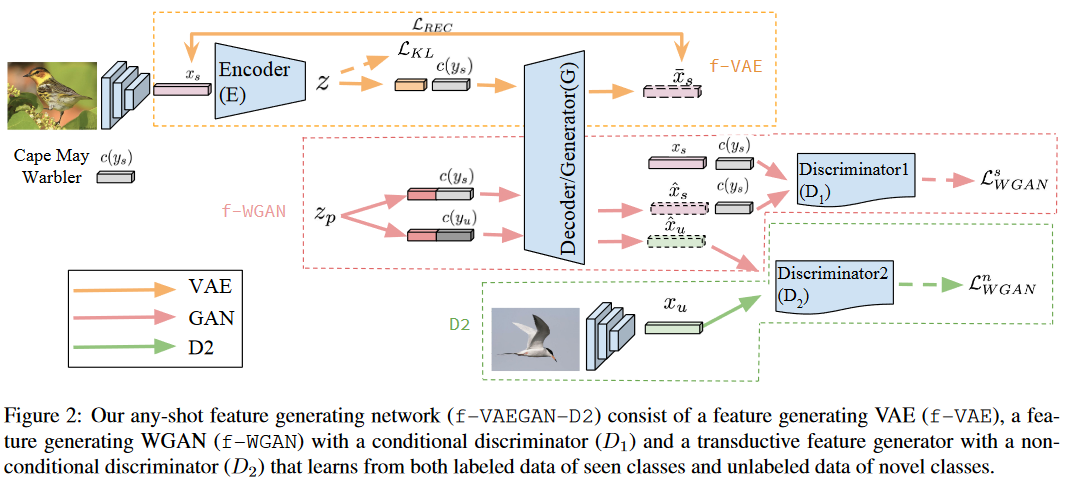
设置

• 对于一组图像\(X={x_1,\ldots,x_l}\cup{x_{l+1},\ldots,x_t}\)，编码在图像特征空间\(\mathcal{X}\)中。
• 一个已见类别标签集\(Y^s\)，一个新类的标签集\(Y^n\)（也就是零样本学习中的未见类别标签集\(Y^u\)）。
• 类别嵌入集合\(C=\{c(y)|\forall y\in Y^s\cup Y^n\}\)（也就是描述图像的信息）编码在语义嵌入空间\(\mathcal{C}\)中。
• 前\(l\)个样本\(x_s\ (s\le l)\)标记为已见类别\(y_s\in Y^s\)，其余点\(x_{\boldsymbol{n}}(l+1\leq n\leq t)\)是未标记的，可能是已见或新类。

在归纳设置中，训练集仅包含已见类别图像的标记样本,即\(X=\{x_1,\ldots,x_l\}\)。在转导设置中，训练集包含标记和未标记样本，即\(X=\{x_1,\ldots,x_l,x_{l+1},\ldots,x_t\}\)。

在零样本学习中，任务是预测属于新颖类别的那些未标记点的标签，即\(f_{zsl}:\mathcal{X}\rightarrow\mathcal{Y}^n\)。而在广义零样本学习中，目标既可以是已见类别也可以来自新类的未标记数据并进行分类，即\(f_{gzsl}:\mathcal{X}\rightarrow\mathcal{Y}^s\cup\mathcal{Y}^n\)。

VAE与WGAN的损失函数

生成器\(G(z,c)\)接受随机噪声\(z_p\)（文中假设\(z_p\sim\mathcal{N}(0,1)\)）和条件\(c\)，生成特征空间\(\mathcal{X}\)上的CNN特征\(\hat{x}\)。判别器D(x,c)判断一对特征和类别嵌入是真实的还是生成的。GAN的优化目标（实际上就是WGAN的损失函数：'Earth-Mover'距离+梯度惩罚项）为：

\[\mathcal{L}_{WGAN}^{s}= \mathbb{E}[D(x,c)]-\mathbb{E}[D(\tilde{x},c)]-\lambda\mathbb{E}[(||\nabla_{\hat{x}}D(\hat{x},c)||_2-1)^2] \]

\(\tilde{x}=G(z,c)\)为生成的特征，\(\hat{x}=\alpha x+(1-\alpha x),\alpha\sim U(0,1)\)，\(\lambda\)为惩罚系数。

编码器\(E(x,c)\)将一对特征\(x\)和作为条件的类别嵌入\(c\)编码为潜在向量\(z\)。VAE的优化目标为：

\[\mathcal{L}_{VAE}^{s} =KL(q(z|x,c)||p(z|c)) -\mathbb{E}_{q(z|x,c)}[\log p(x|z,c)] \]

\(q(z|x,c)\)即为\(E(x,c)\)，表示建模的条件分布；\(p(z|c)\)被假设为\(\mathcal{N}(0,1)\)；\(p(x|z,c)\)等同于解码器\(Dec(z,x)\)。

优化目标设置

图中的编码器\(E(x,c):\mathcal{X}\times\mathcal{C}\rightarrow\mathcal{Z}\)将一对特征和类别嵌入编码为潜在向量。判别器\(D_{1}:\mathcal{X}\times\mathcal{C}\rightarrow\mathbb{R}\)判断一对特征和类别嵌入是真实的还是生成的。整个VAE-GAN的优化目标为：

\[\mathcal{L}_{VAEGAN}^s=\mathcal{L}_{VAE}^s+\gamma\mathcal{L}_{WGAN}^s \]

VAE的Decoder与GAN的Generator共享参数（也就是同一个模块两个名字，就像图中画出的）；上标\(s\)表示该损失仅用于可见类；\(\gamma\)为超参数控制VAE和WGAN损失的权重。

而对于未见类，使用了无条件判别器\(D_2\mathcal{X}\to\mathbb{R}\)区分是真实的还是合成的未见类特征，优化目标为一个WGAN的损失函数：

\[\mathcal{L}_{WGAN}^n=\mathbb{E}[D_2(x_n)]-\mathbb{E}[D_2(\tilde{x}_n)]-\lambda\mathbb{E}[(||\nabla_{\hat{x}_n}D_2(\hat{x}_n)||_2-1)^2] \]

其中\(\tilde{x}_n=G(z,y_n), y_n\in Y^n,\hat{x}_n=\alpha x_n+(1-\alpha x_n),\alpha\sim U(0,1)\)。

\(\hat{x}_n\)的作用是满足梯度惩罚，保证 WGAN 符合 Lipschitz 连续性。 具体来说，\(\hat{x}_n\) 是通过对真实数据样本 \(x_n\) 进行微小的扰动得到的。用\(\alpha\)控制扰动的大小。\(\hat{x}_n\) 通过在 \(x_n\) 周围加入一个小的扰动来近似数据分布的局部结构，从而鼓励判别器对数据的微小变化做出响应。这有助于使判别器在输入空间中是局部 Lipschitz 连续的，从而实现梯度惩罚。

Lipschitz连续定义：对于在实数集的子集的函数 \(f{:}D\subseteq\mathbb{R}\to\mathbb{R}\)，若存在常数\(K\)使得\(|f(a)-f(b)|\leq K|a-b|\quad\forall a,b\in D\)，则称\(f\)符合Lipschitz条件，对于\(f\)最小的常数\(K\)称为 \(f\)的Lipschitz常数。[Source]

\(\mathcal{L}^s_{WGAN}\)的训练依赖语义嵌入的质量并存在域转移问题（缓解域转移问题也是归纳ZSL发展至转导ZSL的重要原因）。于是通过\(\mathcal{L}^n_{WGAN}\)学习CNN特征的边缘分布，为新类提供可转移的CNN特征。因此整个f-VAEGAN-D2优化函数为：

\[\min_{G,E}\max_{D_1,D_2}\mathcal{L}_{VAEGAN}^s+\mathcal{L}_{WGAN}^n \]

其他

图中的随机噪声\(z\sim \mathcal{N}(0,1)\)与类嵌入\(c(y)\)，经过串联后进入生成器，它们的维度相同时，即\(d_z=d_c\)效果较好（没有解释，也许是测试发现的？）。同样，视觉特征和类嵌入串联后进入判别器。\(\mathcal{L}_{REC}\)为二元交叉熵损失函数，表示重构损失。

3. 实验

论文中，对于合成的特征进行解释。图像特征通过上采样生成图片；文本解释通过训练的LSTM生成，LSTM根据图像的平均隐藏层生成类嵌入，得到合成特征的解释。

对于每一块，顶部是原始图像，中部是原始图像真实特征(R)重构结果，底部同一类的合成特征(S)重构结果。

图展示了从真实特征和合成特征获得的解释。我们观察到该模型为可见类和未见类的合成特征生成图像相关和类特定的解释。例如,“King Protea”特征包含有关“红色花瓣和尖尖”的信息，而“Purple Coneflower”特征包含有关“粉红色和向下下垂的花瓣”的信息，这些特征是这种花在视觉上最显着的特征。

另一方面，如图底部所示，对于图像特征缺乏一定细节水平的类，生成的解释存在一些问题，例如重复，例如“喇叭形”和“星形”在同一个句子中和未知单词，例如参见“气球花(Balloon Flower)”的解释。

参考文献

1. Xian, Yongqin, et al. "f-vaegan-d2: A feature generating framework for any-shot learning." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019.