有监督学习——决策树、集成学习
1. 决策树
熵
在热力学中,熵(entropy)被用来衡量系统的不稳定程度。香农在论文《通信的数学原理》中提出信息熵的概念,目的是量化数字信息的价值。
信息熵的定义
香农提出的量化信息方式:
其中:\(P_1,P_2\cdots P_n\)是随机事件每种可能结果的发生概率,因此\(P_1+P_2+\cdots+P_n=1\),熵\(H()\)的结果是一个大于等于零的值。熵越高,信息的不确定性越大,那么这条信息结果的价值越大。
e.g. 现在有三条来自未来的消息,哪条消息更高?
- 一枚均匀硬币的投掷结果。
- 一颗均匀骰子的投掷结果。
- 一颗不均匀骰子的投掷结果(其中一面概率为0.9,其他的概率均为0.02)。
分别计算:
均匀硬币每面的概率为0.5,\(H=-[0.5\times\log_2(0.5)+0.5\times\log_2(0.5)]=1\)
均匀骰子每面的概率是\(\frac{1}{6}\),\(H=-\frac{1}{6}\times\log_2(\frac{1}{6}) \times6\approx2.59\)
不均匀骰子的信息熵:\(H=-[\frac{9}{10}\times\log_2(\frac{9}{10})+\frac{1}{20}\times\log_2(\frac{1}{20})\times 5]\approx 1.22\)
总结下:
- 随机事件结果种类越多,该事件的熵越大。
- 随机事件各种可能发生的结果概率越均匀,则事件熵越大(以事件3为例,即使无人告诉,也容易猜到发生的是概率大的事件)。
基尼指数(Gini index)
信息熵的\(\log\)计算在CPU中较为耗时,因此使用另一个衡量信息价值的指标——基尼指数:
该公式值域\([0,1]\),数值越大表示事件越无序。衡量信息能力略逊于信息熵、但计算完全由乘法和加法组成。
建树策略
决策树的训练是一个利用已有样本从根开始逐步挑选并建树的过程。
例如最开始是寻找一个特征作为根节点,而选择的依据是在用该特征进行数据划分后得到的信息增益最大。
在用某个特征将数据集划分到不同的子树后,所有子树的信息价值(熵/基尼指数)的和必定小于等于原来整体数据集的信息价值,信息增益用来衡量减少的程度。
设有建树函数build(),则递归训练决策树的算法思想:
def build(D=数据集,):
if D中所有数据目标值y都相同: # 本数据集可以作为叶子节点
return
for i in D中所有特征:
计算用i划分子树后获得的信息增益
if 所有的特征都没有大于0的信息增益: # 已经无法再分
return
x(被选择的特征) = 具有最大信息增益的特征
for sub in 按照x划分子树后的数据集: # 递归寻找下一个决策树
build(sub)
上述算法思想还有诸多细节:
- 信息增益如果直接用划分前后的熵差计算,则会导致倾向于分类取值较多的特征(对比掷硬币和掷骰子)。
- 连续值类型的特征如何计算?
- 强制要求每个叶子节点只有一个目标值容易导致预测过拟合,如何适当归并叶子节点(剪枝,prune)?
- 决策树如何处理回归问题?
根据这些问题,决策树衍生了不少的算法,下面为几种影响较大的算法:
- ID3: 只使用熵的信息增益处理离散特征的分类问题。
- C4.5:
使用信息增益比的概念去除先选择多值特征的倾向;
支持连续特征,在计算信息增益比之前首先将其离散化;
在训练后检测训练集的正确分类比,并剪枝产生错误较多的叶子结点。 - CART算法:
使用基尼系数代替熵进行信息增益计算;
只使用二叉树;
提供解决回归问题的能力。
综上,CART比另外两种算法更能适应更多场景。
Python中的 DecisionTreeClassifier 与 DecisionTreeRegressor
scikit-learn在sklearn.tree包中实现了CART模型,分别用DecisionTreeClassifier、DecisionTreeRegressor实现了分类树和回归树。它们的使用方法与其他模型类似。
以下为一些主要的模型初始化参数:
| 参数 | 介绍 |
|---|---|
| criterion | 取值gini或entropy,即使用基尼指数还是熵计算信息增益 |
| max_depth | 树的最大深度 |
| min_sample_split | 继续分裂一个结点最少需要的训练样本数 |
| max_leaf_nodes | 叶子结点的最大总数 |
| min_impurity_decrease | 用于计算叶子结点的最小纯度(即不同目标值样本之间的比值) |
from sklearn.tree import DecisionTreeClassifier # 从tree包引入
# 定义训练数据集
X = [
[20, 30000, 400], [37, 13000, 0],
[50, 26000, 0], [28, 10000, 3000],
[31, 19000, 1500000], [47, 7000, 6000]
]
Y = [1, 0, 0, 0, 1, 0]
# 初始化熵模型训练对象
clf = DecisionTreeClassifier(criterion='entropy')
clf.fit(X=X, y=Y) # 训练
print(clf.predict([[40, 6000, 0]])) # 预测
# [0]
clf.feature_importances_ # 查看特征重要性
# array([0.5, 0.5, 0. ])
可以使用pygraphviz来对决策树进行可视化:
原书是用
graphviz,但笔者进行安装后无法使用,原因是:libexpat.dll找不到,几经波折后找到解决方法。
遂采用更多人推荐的pygraphviz,但在第一次使用过程中也遇到了错误:不支持png、
更多关于pygraphviz的绘画可查看官方文档
import pygraphviz as pgv
import sklearn.tree as tree
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=['age', 'income', 'deposit'],
class_names=['normal', 'VIP'],
filled=True, rotate=True)
graph = pgv.AGraph(dot_data)
graph.draw("mytree.png", prog='dot') # 保存成文件
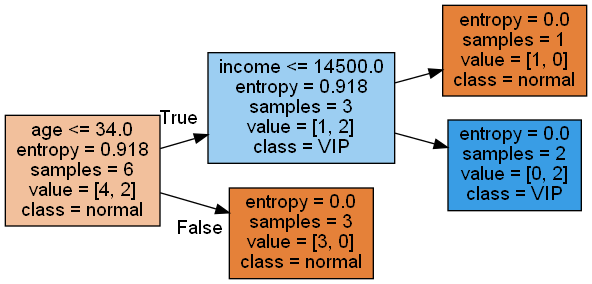
2. 集成学习
集成学习(Ensemble Learning)模型与其他有监督模型的出发点不同:之前介绍的都是模型在给定的训练集上构建算法进行数据拟合;而集成学习着重考虑数据集,将数据集划分为各种子集或权重变换后用较弱的基模型拟合,再综合若干个基模型的预测作为最终整体结果。
在scikit-learn中包括了两类集成学习算法:
- Bagging Method: 若干个基模型在若干个训练子集上进行
互相独立的分别训练,在预测时一次性综合这些基模型的结果。 - Boosting Method: 按迭代的顺序
逐个训练基模型,在每次训练后进行模型预测,并根据测试结果调整下一轮基模型训练时所采用的模型数据,最后预测时仍然使用所有子模型的预测结果得到最终结果。
偏差与方差
有监督学习可以可以将目标归结为对两种系统错误的最小化——偏差(bias)和方差(variance)。
对于一个训练好的模型:\(\hat{f}()\)。
在测试集中测试得到多个错误值:\(Error=\hat{f}(x)-y\),其中\(x\)是测试数据特征,\(y\)是测试数据真实目标值。
如果采用高斯分布拟合这些错误值,最终找到参数\(u\)和\(\sigma^2\),使得\(Error\sim N(u,\sigma^2)\),其中错误期望参数\(u\)可以理解为偏差(bias),\(\sigma^2\)是方差(variance)。
与拟合程度的关系
根据有监督学习预测效果的表现,可发现:偏差对应的是欠拟合(Underfitting);方差对应的是过拟合(Overfitting)。
“偏差越大,欠拟合越严重”容易理解。但怎么理解高方差对应的过拟合?因为方差高意味着:模型对训练数据中的小波动过于敏感,并且可能不能很好地推广到新的数据。
大部分情况下,欠拟合与过拟合不可很好地同时解决,因此各种学习模型和超参数的调整都是调节两者的平衡点。
集成学习意图
对比之前模型的“单独”,集成学习综合各若模型结果,可以学习到若干个这样的错误分布:
弱模型通常有拟合不足的问题,即绝对值较大的偏差、较低或一般的方差。在综合各模型的结果可看成错误高斯分布求平均值过程:
其中,其中\(N\)是弱模型的数量。
由于偏差的符号有正有负,因此若干个模型的偏差均值可以将绝对值降低;对于方差,弱模型的方差并不高,因此综合后仍在较低水平。
随机森林
随机森林(Random Forrest)是Bagging Method的典型代表,是使用决策树作为基模型的集成学习方法。
集成框架
随机森林在训练过程中进行随机抽样,分别进行训练后形成若干个小的决策树。对于分类问题,通过这些基决策树投票完成;对于回归问题,通过基决策树结果求平均完成。
随机森林模型中的决策树一般采用有较大偏差和较小方差的“弱模型”,对比普通决策树,具体在以下方面:
- 样本裁剪:通过随机采样每个弱模型只训练部分样本数据。
- 特征采样:每个基模型的决策树只选用数据特征中的一部分进行训练和预测,随机抽样保证了所有特征都能被部分弱模型学习到。
- 小树:特征和样本数量的原因,导致弱模型的决策树高度不高,因此不需要像一般决策树那样过拟合和剪枝。
有放回采样
有放回采样(bootstrap)是指每次抽取一个样本放入子集后,将样本仍保留在被采样空间,使它仍可能再次被采样到。这样能生成与训练样本整体不同的数据分布,等于扩充了训练样本空间,因此通过bootstrap采样能狗训练出适应性更强的模型。
Out-of-Bag Estimation
Out-of-Bag Estimation简称OOB,它是指基模型评估预测的数据只采用训练集之外的数据。
RandomForestClassifier和RandomForestRegressor
在sklearn.ensemble包中提供了随机森林模型RandomForestClassifier和RandomForestRegressor,使用方式与其他模型相似。在模型参数方面,决策树作为基模型,因此在模型初始化过程中保留了所有决策树模型(DecisionTreeClassifier/DecisionTreeRegressor)相关参数。此外还提供抽样方式和OOB评估的配置参数:
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
iris = load_iris() # 导入iris数据库
clf = RandomForestClassifier(n_estimators=20, bootstrap=True, oob_score=True)
clf.fit(iris.data, iris.target) # 训练
clf.oob_score_ # 在初始化指定oob_score=True才能访问
# 0.96
| 参数 | 解释 |
|---|---|
| n_estimators | 定义基模型数量 |
| bootstrap=True | 使用有放回采样 |
| oob_scare=True | 指定在训练后进行OOB测试,训练后的oob_score_属性表示准确性评估 |
自适应增强
自适应增强(Adaptive Boosting,或称AdaBoost)是Boosting Method典型代表。Boosting Method类算法不是通过随机抽样产生每个基模型的训练集,而是通过训练集中每个样本的权重使得每次迭代在不同的训练集上运行
算法原理
在AdaBoost的每次迭代中都使用了全部训练样本,但训练样本中的每个样本都被赋予了权值,因此基模型必须支持基于样本权值的学习方法。
基于样本权值训练是指建立模型时,更关注匹配权值高的样本,常见的如支持向量机、朴素贝叶斯等。
第一次迭代时,训练集中的每个样本将被赋予相同的权值,经过训练和评估后AdaBoost会更新训练集中的样本,被预测正确的样本权值减少,被预测错误的样本权值增加。如此往复。
基模型是随着迭代增加逐步进化的,因此,在最终决策后生成的基模型往往比之前的基模型决策权更大。与Bagging Method相比,最终的预测结果采用基模型间的“加权”投票/平均。
AdaBoostClassifier和AdaBoostRegressor
sklearn.ensemble中提供了AdaBoostClassifier和AdaBoostRegressor分别用于AdaBoost的分类和回归问题。以下为几个它们独特的初始化参数:
| 参数 | 介绍 |
|---|---|
| base_estimator | 基模型,默认为决策树,也可选为贝叶斯 |
| n_estimators | 迭代次数,默认为50 |
| learning_rate | 学习率,取值0~1,用于控制最终决策时各基模型的权重,该值越大,后产生的基模型所占模型权重越大 |
| algorithm | 提升算法,可选择SAMME或SAMME.R,该算法用于定义在每次迭代后如何更新训练样本权重。SAMME按照分类错误率更新权重;SAMME.R按照预测概率更新权重。 |
由于SAMME只适用于离散问题,因此
algorithm仅存在于AdaBoostClassifier的初始化参数中,而AdaBoostRegressor默认使用SAMME.R算法。
score()评估函数
AdaBoost使用全部的数据进行训练,因此没有OOB评估,只能使用测试集在训练后评估。scikit-learn对大多数监督学习模型都提供了score()函数,用于评估测试集的预测准确率,输入测试数据,输出<=1的评估值表示准确率。
from sklearn.datasets import load_iris
from sklearn.ensemble import AdaBoostClassifier # 导入模型类
iris = load_iris()
from sklearn.utils import shuffle
X, Y = shuffle(iris.data, iris.target) # 对数据进行随即洗牌
# 初始化以GaussianNB作为基模型的AdaBoost分类器
from sklearn.naive_bayes import GaussianNB
clf = AdaBoostClassifier(GaussianNB())
clf.fit(X[:-20], Y[:-20]) # 训练
clf.score(X[-20:], Y[-20:]) #评估
# 0.95
scikit-learn中还实现了其他ensemble模型,包括GradientBoosting、Voting等。
参考文献
[1]刘长龙. 从机器学习到深度学习[M]. 1. 电子工业出版社, 2019.3.




